人工智能与机器学习-梯度下降法
人工智能与机器学习-梯度下降法
一、梯度下降法概述
梯度下降法(Gradient descent)是一个一阶最优化算法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。
二、梯度下降法直观理解
以人下山为例,要到达最低点,需要以下步骤:
第一步,明确自己现在所处的位置
第二步,找到相对于该位置而言下降最快的方向
第三步,沿着第二步找到的方向走一小步,然后到底一个新的位置,这时候的位置就比原来更低
第四步,又明确当前所处位置,即回到第一步
第五步,到底最低点后就停下
基于以上步骤,就能够找到最低点,以下图为例
三、多元函数的梯度下降解法
以y(x)函数为例,这个函数具有n+1个自变量:
![]()
首先需要设置下降的初始位置,随意设置即可:

接下来需要对每一个自变量求偏导:
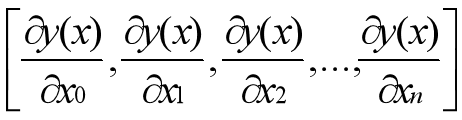
将设置的初始值代入偏导的公式,接下来进行迭代的公式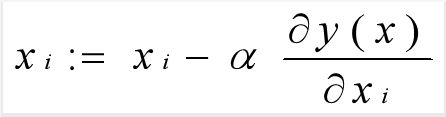
上式中的α为学习率,也可叫做步长
四.实例
1、Python与Excel分别使用梯度下降法求解极小值与极小点
(1)、Excel使用梯度下降法求解极小值与极小点
需要设置下降的起始位置与学习率的值:
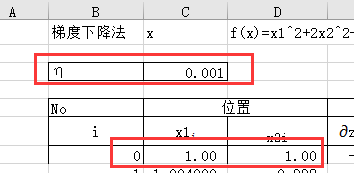
通过设置的起始位置去计算自变量的偏导、偏导与学习率的乘积以及最终的函数值:
已经知道第一行的信息,也就可以计算出第二行的信息,然后根据第二行的信息进行迭代求极值,因为第一行的计算公式与第二行的计算公式有所不同,但第二行与后面的计算公式相同,因此还需要求得第二行的信息: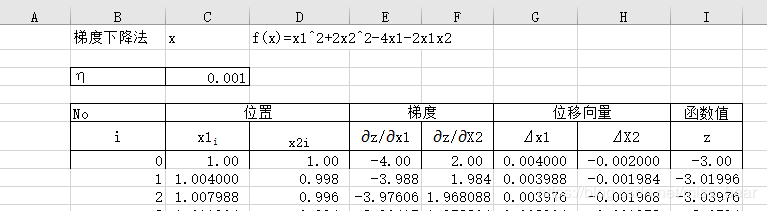
后面的迭代可以采用excel中的复制功能即可,当函数值收敛的时候停止迭代,因为学习率取得比较小,因此迭代的次数就会比较多。

最终迭代出来的极小值为-8,极小点为(4,2),在迭代多次x1的值应该是等于4的
(2)、Python计算极小值与极小点并画出图像
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
from mpl_toolkits.mplot3d import Axes3D
import warnings
# 解决中文显示问题
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
%matplotlib inline
def f2(x1,x2):
return x1 ** 2+2*x2 ** 2-4*x1-2*x1*x2
X1 = np.arange(-4,4,0.2)
X2 = np.arange(-4,4,0.2)
X1, X2 = np.meshgrid(X1, X2) # 生成xv、yv,将X1、X2变成n*m的矩阵,方便后面绘图
Y = np.array(list(map(lambda t : f2(t[0],t[1]),zip(X1.flatten(),X2.flatten()))))
Y.shape = X1.shape # 1600的Y图还原成原来的(40,40)
%matplotlib inline
#作图
fig = plt.figure(facecolor='w')
ax = Axes3D(fig)
ax.plot_surface(X1,X2,Y,rstride=1,cstride=1,cmap=plt.cm.jet)
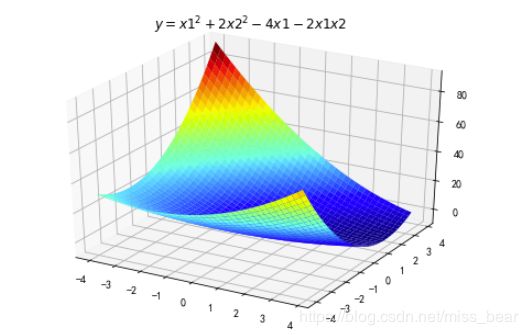
ax.set_title(u'$ y = x1^2+2x2^2-4x1-2x1x2 $')
plt.show()
# 二维原始图像
def f2(x1, x2):
return x1 ** 2+2*x2 ** 2-4*x1-2*x1*x2
## 偏函数
def hx1(x1, x2):
return 2* x1-4-2*x2
def hx2(x1, x2):
return 4*x2-2*x1
x1 = 1
x2 = 1
alpha = 0.0011
#保存梯度下降经过的点
GD_X1 = [x1]
GD_X2 = [x2]
GD_Y = [f2(x1,x2)]
# 定义y的变化量和迭代次数
y_change = f2(x1,x2)
iter_num = 0
while(y_change < 1e-10 and iter_num < 10000) : #此处可以设置迭代的次数以及y的变化量小于多少时停止迭代
tmp_x1 = x1 - alpha * hx1(x1,x2)
tmp_x2 = x2 - alpha * hx2(x1,x2)
tmp_y = f2(tmp_x1,tmp_x2)
f_change = np.absolute(tmp_y - f2(x1,x2))
x1 = tmp_x1
x2 = tmp_x2
GD_X1.append(x1)
GD_X2.append(x2)
GD_Y.append(tmp_y)
iter_num += 1
print(u"最终结果为:(%.5f, %.5f, %.5f)" % (x1, x2, f2(x1,x2)))
print(u"迭代过程中X的取值,迭代次数:%d" % iter_num)
print(GD_X1)
# 作图
fig = plt.figure(facecolor='w',figsize=(20,18))
ax = Axes3D(fig)
ax.plot_surface(X1,X2,Y,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.plot(GD_X1,GD_X2,GD_Y,'ko-')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
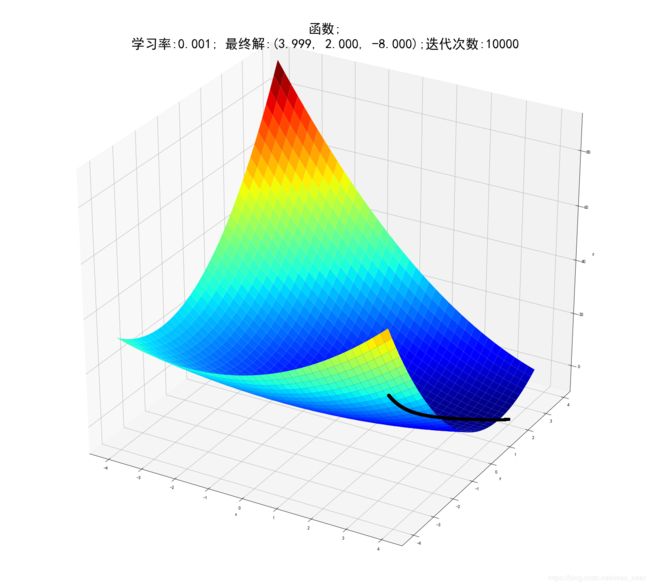
ax.set_title(u'函数;\n学习率:%.3f; 最终解:(%.3f, %.3f, %.3f);迭代次数:%d' % (alpha, x1, x2, f2(x1,x2), iter_num),fontsize=30)
plt.show()
最终结果为:(3.99942, 1.99964, -8.00000)
迭代过程中X的取值,迭代次数:10000
[1, 1.0044, 1.00878548, 1.013156514536, 1.0175131777223392, 1.021855543254118, 1.0261836844096073, 1.0304976740526408.........]
2、梯度下降法求解多元线性回归方程式参数并与最小二乘法求得参数进行比较
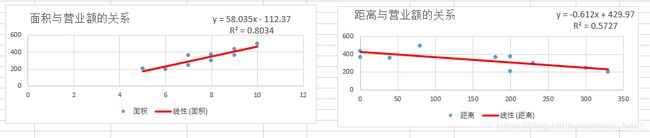
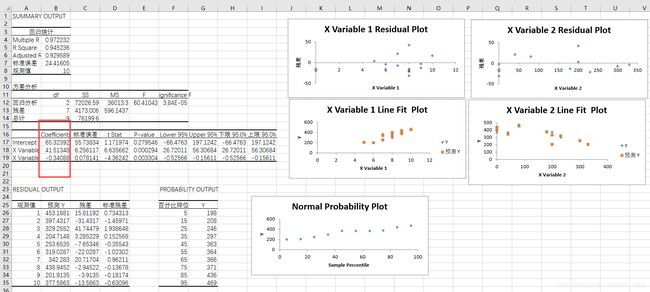
(1)、最小二乘法
①、Excel得出的结果
②、Python计算出来的结果与画出的图像
#导入需要的库
from sklearn import linear_model #表示,可以调用sklearn中的linear_model模块进行线性回归。
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
#读入本地数据
data=pd.read_excel('media/作业2.xlsx')
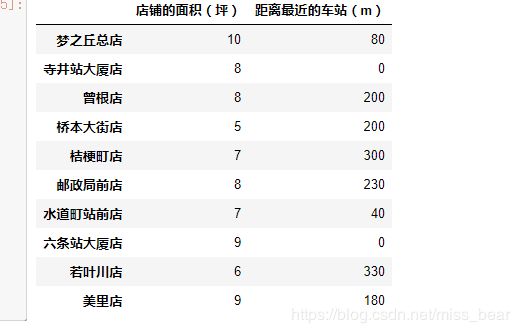
x=data[['店铺的面积(坪)','距离最近的车站(m)']]
x
y=data['月营业额(万日元)']
y
梦之丘总店 469
寺井站大厦店 366
曾根店 371
桥本大街店 208
桔梗町店 246
邮政局前店 297
水道町站前店 363
六条站大厦店 436
若叶川店 198
美里店 364
Name: 月营业额(万日元), dtype: int64
model=linear_model.LinearRegression()
model.fit(x,y)
#调用sklearn库求出常数与未知数
a1=model.coef_[0]
a2=model.coef_[1]
b=model.intercept_
print("第一个未知数a1="+str(a1)+";第二个未知数a2="+str(a2)+";常数b="+str(b))
第一个未知数a1=41.513478256438496;第二个未知数a2=-0.3408826856636194;常数b=65.32391638894819
#打印回归方程
print("多元线性回归y="+str(a1)+"*x1"+str(a2)+"*x2+"+str(b))
多元线性回归y=41.513478256438496*x1-0.3408826856636194*x2+65.32391638894819
#支持中文
from pylab import mpl
mpl.rcParams['font.sans-serif']=['FangSong']
mpl.rcParams['axes.unicode_minus']=False
sns.pairplot(data, x_vars=['店铺的面积(坪)','距离最近的车站(m)'], y_vars='月营业额(万日元)',height=8,size=4, aspect=1.5,kind = 'reg')
plt.show()
月营业额与距离车站的距离和店铺面积的关系,可以看出,与车站距离成反比,而与店铺面积成正比。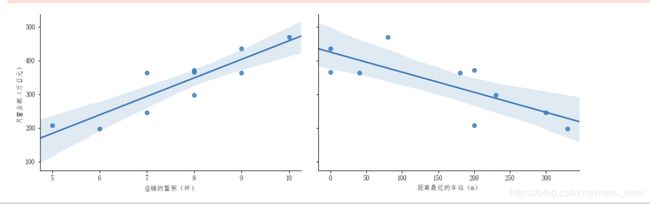
(2)、梯度下降法求解多元线性回归方程式
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
data=np.genfromtxt('media/车站问题.csv',delimiter=',')
x_data=data[:,:-1]
y_data=data[:,2]
#定义学习率、斜率、截据
#设方程为y=theta1x1+theta2x2+theta0
lr=0.00001
theta0=0
theta1=0
theta2=0
#定义最大迭代次数,因为梯度下降法是在不断迭代更新k与b
epochs=10000
#定义最小二乘法函数-损失函数(代价函数)
def compute_error(theta0,theta1,theta2,x_data,y_data):
totalerror=0
for i in range(0,len(x_data)):#定义一共有多少样本点
totalerror=totalerror+(y_data[i]-(theta1*x_data[i,0]+theta2*x_data[i,1]+theta0))**2
return totalerror/float(len(x_data))/2
#梯度下降算法求解参数
def gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs):
m=len(x_data)
for i in range(epochs):
theta0_grad=0
theta1_grad=0
theta2_grad=0
for j in range(0,m):
theta0_grad-=(1/m)*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta2)+y_data[j])
theta1_grad-=(1/m)*x_data[j,0]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
theta2_grad-=(1/m)*x_data[j,1]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
theta0=theta0-lr*theta0_grad
theta1=theta1-lr*theta1_grad
theta2=theta2-lr*theta2_grad
return theta0,theta1,theta2
#进行迭代求解
theta0,theta1,theta2=gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs)
print("多元线性回归方程为:y=",theta1,"X1+",theta2,"X2+",theta0)
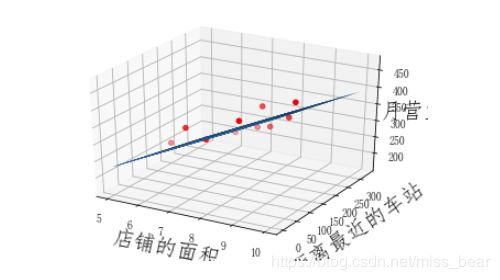
ax=plt.figure().add_subplot(111,projection='3d')
ax.scatter(x_data[:,0],x_data[:,1],y_data,c='r',marker='o')
x0=x_data[:,0]
x1=x_data[:,1]
#生成网格矩阵
x0,x1=np.meshgrid(x0,x1)
z=theta0+theta1*x0+theta2*x1
#画3d图
ax.plot_surface(x0,x1,z)
ax.set_xlabel('店铺的面积',fontsize=20)
ax.set_ylabel('距离最近的车站',fontsize=20)
ax.set_zlabel("月营业额",fontsize=20)
plt.show()
多元线性回归方程为:y= 45.0533119768975 X1+ -0.19626929358281256 X2+ 5.3774162274868
(3)、对比分析
通过与最小二乘法的结果进行对比分析,发现梯度下降法计算出来的误差比较大,精度比较低。而最小二乘法无论是借助sklearn库还是借用公式推导得出的结果都是比较精确的!