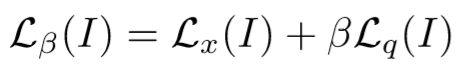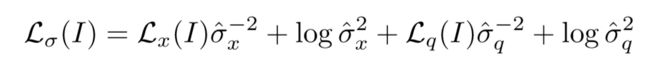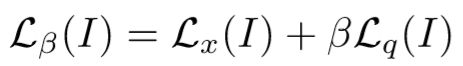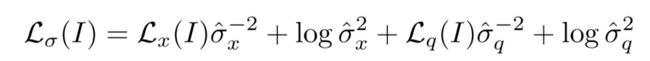PoseNet2：Geometric loss functions for camera pose regression with deep learning 论文笔记
剑桥大学 2017.5 相机重定位，indoor, outdoor，RGB，RGBD
个人总结：
这篇论文是posenet 的损失函数改进版本，但是性能得到了非常大的提升。论文很多细节都讲得非常好，非常详细清晰的说明了为何要选择这种函数/表示（比如选择四元数作为角度量的表示方法，r范数r的确定等）以及要考虑的因素（如是否为单射，结果空间的大小），这些细节往往决定了网络是否收敛以及最终的性能上限。在分析所选择的度量/函数时需要用到大量数学知识。
此外本文的实验比较细致，比如在讨论超参数β时通过实验发现分开模块训练反而会导致性能降低；以及通过实验得到 “β was an approximate function of the scene geometry“的intuition ，这样超参数β的意义就非常明了了。
1.论文摘要：
posenet使用简单的损失函数训练，其超参数需要finetuning
本文探究了用于学习相机位姿的基于几何学和场景重投影误差的简单损失函数。此外提出了一种自动学习用于回归位置损失和朝向损失的二者权重的方法。
利用几何信息，本文方法显著提高了posenet在室内以及室外数据集上的性能
2. 简介&相关工作：
传统基于sift特征的方法：变化场景下点云特征不够鲁棒，不能捕获全局上下文特征
posenet：预测相机位姿的端到端的训练模型，相比sift特征方法更加鲁棒，可以捕获上下文特征；速度也快；可扩展性强，不需要大型地标数据库。
posenet的缺点在于：输出位姿相比其他基于几何方法不够精确，论文认为原因在于posenet只单纯地把端到端的训练方法用在了相机重定位上，而丢弃了几何信息。
论文希望使用多视角几何方法的现有成果进一步提高posenet的性能
论文贡献：
- 将几何损失项融合进 posenet 的损失函数，提高了其性能
- 使用有监督学习回归相机位置和旋转量并非易事，需要权重参数来平衡这两项。posenet中该超参数不可选择， 本文方法移除了该超参数，直接从数据中优化。
3.相机位姿回归模型（Model for camera pose regression）
模型输入：RGB图像，I；输出位姿预测ˆP，对应真值p；
其中位姿P = [x,q]，x: 位置，q: 朝向（四元数形式）
3.1 模型结构
本文使用GOOGLEnet作为backbone。事实上使用任何图像分类模型都可以用以下流程化的改造步骤修改网络使其作为本模型的backbone：
- 去除最后全连接层和softmax层
- 增加一个输出为7维的全连接层，（位置（3）+ 朝向（4））
- 插入一个归一化层将朝向四元数转换到标准长度
3.2 位姿表示
机器学习一个需要重要考虑的问题是其输出的解空间大小。
对于相机位置可以很容易得在笛卡尔坐标系空间中得到，相比之下朝向就比较复杂了。
作者实验了多种角度参数化的方法来表示朝向量：欧拉角，axis-angle，SO(3) rotation matrices，四元数。
- 欧拉角：可解释，但是由于2Pi的周期同一角度有无数个表示，不是单射映射。
- axis-angle：同样受限于周期性的性质，表示不唯一
- SO(3) rotation matrices：过参数化的旋转量表示，旋转矩阵的解空间是一个特殊正交化向量组，因此当通过反向传播学习SO（3）表示时，很难实施正交性约束。
- 四元数：通过将任意四维向量归一化为单位长度，可以很容易地将其映射到合法的四元数。这比旋转矩阵所需的正交化过程更简单。四元数是旋转角度的连续平滑表示。
综上，选择了四元数作为朝向参数化的方式，其唯一的缺点是：每个旋转有两个映射，每个半球一个。3.3.1介绍了如何调整损失函数来补偿这一点
3.3 损失函数
3.3.1 坐标和朝向
-
使用r-范数回归相机三维坐标：
-
使用四元数回归相机朝向：
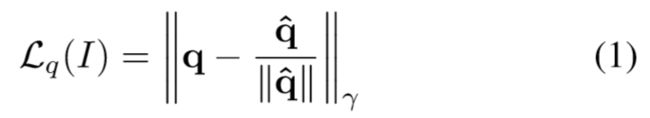
这里输出的q应该是单位圆向量，但是实验中发现q非常接近真值，因此没有加入球形约束。为了解决四元数q与-q相同的问题，论文将四元数的输出限制到一个半球中，使得没一个旋转角度只对应一个四元数。
3.3.2 同时学习坐标和朝向
超参数β用于平衡两个函数项的尺度和单位差异，尽可能保持两项相同
作者发现将两项分开来训练会导致性能下降，原因在于位置和朝向信息会互相辅助预测结果。
因此超参数β的确定就显得很重要，实验发现在户外需要将β调大一点，因为位置误差项对应变大。最后通过实验测算出室内β在 120 to 750，户外 250 to 2000。
但是完成一次测验需要花费数天，因此作者提出了一种不需要该超参数的训练方法。
3.3.3 学习权重β
使用 homoscedastic uncertainty （同方差不确定性）来衡量不确定性，同方差不确定性不依赖于输入数据分布。详见论文： Multi-task learning using uncertainty to weigh losses for scene geometry and semantics
具体的损失函数： 
-
函数第一项（残差）：方差σ^2（即不确定性）越大，残差越小
-
第二项（正则项）：即方差项，防止网络预测出无穷大值以及0值
由于角度四元数在单位尺度，因此其方差σ^2_q 相较于位置方差σ^2_x 要小得多。
因此在实际中网络学习的是对数后的方差项（s=logσ^2），因为其更加稳定：
数学上该损失函数与上面的相同，但是避免了除以0，作者发现这一损失对模型初始化选择是非常有帮助的。
3.3.4 根据几何重投影误差学习
几何重投影误差是一种天然编码了定位和旋转误差的损失函数（只要计算从投影后和原图的像素点误差就可以了）
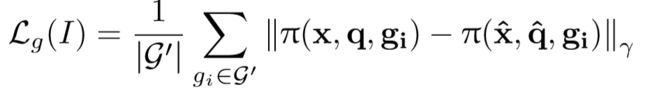
其中：
-
g：3D点云；(u,v)T:对应在2D图像中的位置
-
x,q：相机位置和朝向；
-
π(x,q,g)：映射函数，将三维点云映射到2D图像，具体的：
K为相机内参矩阵，R是旋转四元数q对应的旋转矩阵
-
g’是所有点云的集合g的子集，由图像I中可见的点云构成
有意思的是这个损失函数适用于任意的相机模型，只要损失中使用的相机内参是相同的即可，所以作者选择直接用单位阵代替内参矩阵
论文指出之前的超参数β是在拟合场景的几何特征，例如在远距离场景，旋转的权重相较于位置变得更加重要。
需要指出的是，几何重投影误差要求场景几何信息已知，即输入需要深度信息或使用ＳＦＭ
3.3.5 回归归一化
这里具体介绍如何却选择r-范数：|| ||r
论文中选择了1-范数
4.实验
缩放输入图像到最短边为256，归一化像素值到[-1,1]
4.1 数据集
Cambridge Landmarks
7 Scenes
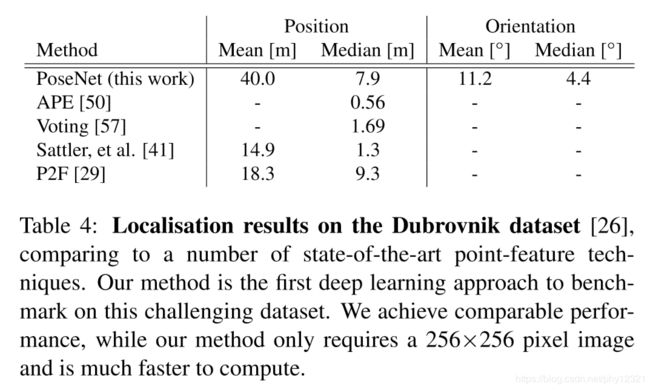
Dubrovnik6K
4.2 损失函数对比
一共有三个：
- 使用了权重超参数β的loss：
- 使用同方差不确定性建模的loss：
- 使用几何重投影误差的loss：
结果说明：
- 使用了对同方差不确定性建模的损失函数的结果 优于 使用了权重超参数的损失函数
- 几何重投影loss在随机初始化条件下无法收敛，会困于局部极小值。
- 几何重投影loss可以进一步提高同方差不确定性loss的性能，即：挑选性能最好的同方差不确定性loss模型，用几何重投影loss进行finetune（在场景几何是已知的情况下，即由RGBD数据或者使用SFM），这样训练的模型性能最佳
4.3 地标定位精度
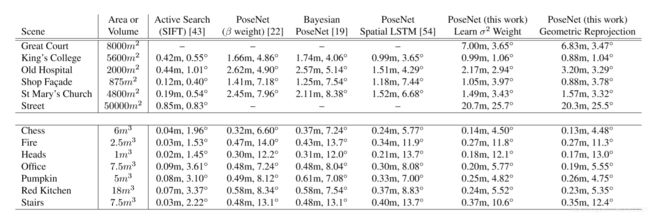
4.4 与基于SIFT特征的方法对比
对比Active Search ，posenet2要求的输入分辨率更低，速度更快。
对比基于几何技术的SIFT方法，posenet2的精度仍然有待提高。作者认为这是由于训练数据太少导致。但是posenet2的速度相比之下要更快。
5.结论
替换了posenet原来的需要超参数的loss函数，提出了二阶段的训练策略以及对应的损失函数