数据结构 线性结构篇——栈和队列
文章目录
- 一、栈
- 1.1 什么是栈
- 1.2 栈的应用
- 1.2.1 无处不在的撤销(undo)操作
- 1.2.1 计算机程序调用的系统栈
- 1.3 栈的实现
- 1.4 栈的时间复杂度
- 二、队列
- 2.1 队列认识
- 2.2 数组队列的实现(顺序存储)
- 2.2.1 接口实现
- 2.2.2 接口类实现
- 2.2.3 执行结果
- 2.2.4 数组队列复杂度分析
- 2.2.4 数组队列的问题
- 2.3 队列的实现(循环队列)
- 2.3.1 循环队列
- 2.3.1 循环队列编码实现
- 2.3.2 循环队列时间复杂度
- 2.3 顺序存储和循环队列性能对比
一、栈
1.1 什么是栈
- 栈是一种线性架构
- 相比数组,栈对应的操作是数组的子集
- 栈只能从一端添加元素,也只能从一端取出元素,最先放入堆栈中的内容最后被拿出来,最后放入堆栈中的内容最先被拿出来, 被称为 先进后出 、后进先出。
- 这里说的一端指的就是 栈顶,删除与添加均在栈顶进行操作
如下图所示:
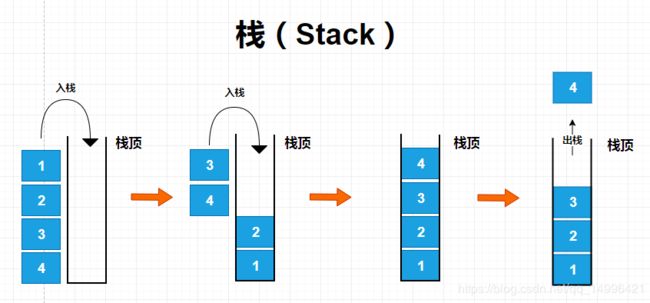
在上图中我们可以看到栈是一种后进先出的数据结构,也就是 Last In First Out(LIFO) ,我们经常看到有 LIFO 找个单词的时候,就是说这是一种后进先出的数据结构,在计算机的世界里,栈拥有着不可思议的作用,接下来我们就来聊一聊,栈的应用。
1.2 栈的应用
1.2.1 无处不在的撤销(undo)操作
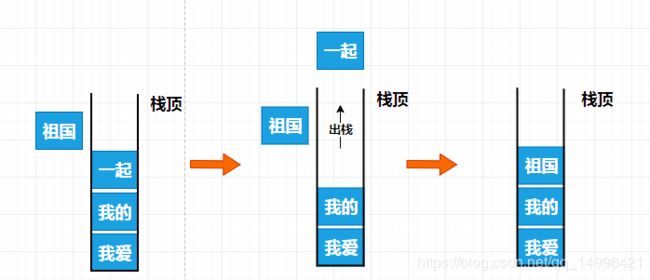
栈在我们计算机的世界里,都有哪些操作呢?不管我们是用开发工具,还是文本编辑,我们都会用一个很常用的操作 (undo操作) ,也就是我们常用的 撤销,当我们打字打快了,打错了,我们只需要按住ctrl + z,就可以将我们输入的文字撤销掉,那么栈是如何在撤销中工作的,比如我们想打我爱我的祖国,这几个字,但是我们打完 我爱我的,准备打祖国的时候,不小心打成了 一起,于是我们就可以进行 撤销操作,将我们的 一起,进行出栈操作,然后在将 祖国添加到我们的栈里面,这样就完成了一次栈在撤销中的工作。
1.2.1 计算机程序调用的系统栈
比如我有下面一段代码:
public static void A(){
System.out.println("A start");
B();
System.out.println("A end");
}
public static void B(){
System.out.println("B start");
C();
System.out.println("B end");
}
public static void C(){
System.out.println("C end");
}
首先我们会先进入 方法 A(),打印输出语句 A start,将方法 A(),作为第一个栈,进行入栈操作,放入我们的系统栈中,然后进入方法 B(),打印输出语句 B start,将方法 B(),作为第二个栈进行入栈操作,再进入方法 C(),打印我们的 C end,到这里入栈操作已经完成了,我们就会从我们的栈里面去取我们刚才入栈的方法,因为 B() 方法是最后一个入栈的,遵循栈 先进后出 的原则,首先我们取出 B() 方法,进行 出栈操作,打印输出语句 B end,最好我们取出A() 方法,进行 出栈操作,打印输出语句 A end,以上整个就是我们程序调用系统栈的操作,我们来看下打印结果:
A start
B start
C end
B end
A end
执行流程如下图所示:

如果能够合理的运行栈,会对我们的程序起很好的作用,还有一些栈的应用,比如 递归算法
1.3 栈的实现
这里我们关于数组部分,可以查看上一篇:动态数组
首先我们需要以下几个栈元素:
int getSize(); // 获取栈的元素多少
boolean isEmpty(); //查看栈是否为空
void push(E e); //添加栈元素
E pop(); //出栈
E peek(); //查看栈顶元素是多少
具体方法实现:
自定义数组类:
public class Array<E> {
private E[] data;
private int size;
// 构造函数,传入数组的容量capacity构造Array
public Array(int capacity){
data = (E[])new Object[capacity];
size = 0;
}
// 无参数的构造函数,默认数组的容量capacity=10
public Array(){
this(10);
}
// 获取数组的容量
public int getCapacity(){
return data.length;
}
// 获取数组中的元素个数
public int getSize(){
return size;
}
// 返回数组是否为空
public boolean isEmpty(){
return size == 0;
}
// 在index索引的位置插入一个新元素e
public void add(int index, E e){
if(index < 0 || index > size)
throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
if(size == data.length)
resize(2 * data.length);
for(int i = size - 1; i >= index ; i --)
data[i + 1] = data[i];
data[index] = e;
size ++;
}
// 向所有元素后添加一个新元素
public void addLast(E e){
add(size, e);
}
// 在所有元素前添加一个新元素
public void addFirst(E e){
add(0, e);
}
// 获取index索引位置的元素
public E get(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Get failed. Index is illegal.");
return data[index];
}
public E getLast(){
return get(size - 1);
}
public E getFirst(){
return get(0);
}
// 修改index索引位置的元素为e
public void set(int index, E e){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Set failed. Index is illegal.");
data[index] = e;
}
// 查找数组中是否有元素e
public boolean contains(E e){
for(int i = 0 ; i < size ; i ++){
if(data[i].equals(e))
return true;
}
return false;
}
// 查找数组中元素e所在的索引,如果不存在元素e,则返回-1
public int find(E e){
for(int i = 0 ; i < size ; i ++){
if(data[i].equals(e))
return i;
}
return -1;
}
// 从数组中删除index位置的元素, 返回删除的元素
public E remove(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Remove failed. Index is illegal.");
E ret = data[index];
for(int i = index + 1 ; i < size ; i ++)
data[i - 1] = data[i];
size --;
data[size] = null; // loitering objects != memory leak
if(size == data.length / 4 && data.length / 2 != 0)
resize(data.length / 2);
return ret;
}
// 从数组中删除第一个元素, 返回删除的元素
public E removeFirst(){
return remove(0);
}
// 从数组中删除最后一个元素, 返回删除的元素
public E removeLast(){
return remove(size - 1);
}
// 从数组中删除元素e
public void removeElement(E e){
int index = find(e);
if(index != -1)
remove(index);
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append(String.format("Array: size = %d , capacity = %d\n", size, data.length));
res.append('[');
for(int i = 0 ; i < size ; i ++){
res.append(data[i]);
if(i != size - 1)
res.append(", ");
}
res.append(']');
return res.toString();
}
// 将数组空间的容量变成newCapacity大小
private void resize(int newCapacity){
E[] newData = (E[])new Object[newCapacity];
for(int i = 0 ; i < size ; i ++)
newData[i] = data[i];
data = newData;
}
}
接口类:
public interface Stack<E> {
int getSize();
boolean isEmpty();
void push(E e);
E pop();
E peek();
}
接口实现:
import com.lyy.datasty.Array;
/**
* @program: Data-Structures
* @ClassName ArrayStack
* @description:
* @author: lyy
* @create: 2019-11-20 21:52
* @Version 1.0
* 用户不能看栈中间的元素,只能看到栈顶的元素
**/
public class ArrayStack<E> implements Stack<E>{
Array<E> array;
public ArrayStack(int capacity){
array = new Array<>(capacity);
}
public ArrayStack(){
array = new Array<>();
}
@Override
public int getSize() {
return 0;
}
@Override
public boolean isEmpty() {
return array.isEmpty();
}
public int getCapacity(){
return array.getCapacity();
}
@Override
public void push(E e) {
array.addLast(e);
}
@Override
public E pop() {
return array.removeLast();
}
@Override
public E peek() {
return array.getLast();
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append("Stack:");
res.append('[');
for (int i = 0; i < array.getSize(); i++) {
res.append(array.get(i));
if(i != array.getSize() - 1)
res.append(",");
}
res.append("] top");//哪里是栈顶
return res.toString();
}
}
测试结果:
Stack: [0] top
Stack: [0, 1] top
Stack: [0, 1, 2] top
Stack: [0, 1, 2, 3] top
Stack: [0, 1, 2, 3, 4] top
Stack: [0, 1, 2, 3] top
从结果中我们可以看到,我们每循环一次就添加一条数据,这里为了好让我们知道哪一个是 栈顶,我们在最后一个添加的数据那里,加了一个 top ,最新增加的数据,就是我们的栈顶,当我们添加完成后,可以看到栈数据为:[0, 1, 2, 3, 4] top,当我们出栈一个数据后,我们就可以看到 栈顶数据 4 就没有了,以上就是对于栈实现的代码,感兴趣的小伙伴可以自己实现一遍,源码在最后我会放在 github上,有兴趣的小伙伴记得下载。
1.4 栈的时间复杂度
ArrayStack:
| 方法 | 时间复杂度 |
|---|---|
| void push(E e) | O(1) 均摊 |
| E pop() | O(1) 均摊 |
| E peek() | O(1) |
| int getSize() | O(1) |
| boolean isEmpty() | O(1) |
二、队列
2.1 队列认识
- 队列与栈一样是一种线性结构,因此以常见的线性表如数组、链表作为底层的数据结构。
- 相比数组,队列对应的操作是数组的子集
- 队列只能从一端(队尾)添加元素,只能从一端(队首)取出元素,也就是队尾添加元素,在队头删除元素
- 队列是一种先进先出的数据结构(先到先得)
- 队列列中的数据元素遵循“先进先出”(First In First Out)的原则,简称 FIFO 结构。
- 队列是一个 先进先出的线性表,相应的也有
顺序存储 和 链式存储两种方式。
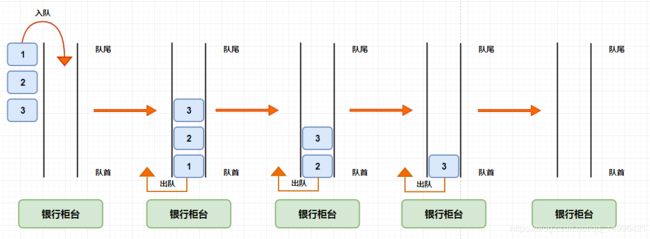
在队列中,新添加的一端为 队尾 ,另一端为 队首 ,当一个元素从队尾进入队列时,一直向队首移动,直到它成为移除的元素为止。这种 先进先出(FIFO) 模式,在我们生活中也随处可见,比如:我们去银行柜台取钱,我们在取钱之前就要先去取号,先做 入队操作,也就是我们队列中的在 队尾添加元素,新来的人等待排队,等待前面的人处理完,当前面取号的人在柜台处理完之后,就会叫下一个号码,这个过程就是 出队操作,只有当在我们前面的人,都处理完之后才会轮到我们。
2.2 数组队列的实现(顺序存储)
首先我们需要以下几个栈元素:
int getSize(); // 获取队列的元素多少
boolean isEmpty(); //查看队列是否为空
void enqueue(E e); //添加队列元素
E dequeue(); //删除队列队首元素
E getFront(); //获取队首队列元素
2.2.1 接口实现
public interface Queue<E> {
int getSize();
boolean isEmpty();
void enqueue(E e);
E dequeue();
E getFront();
}
2.2.2 接口类实现
public class ArrayQueue<E> implements Queue<E> {
private Array<E> array;
public ArrayQueue(int capacity){
array = new Array<>(capacity);
}
public ArrayQueue(){
array = new Array<>();
}
@Override
public int getSize(){
return array.getSize();
}
@Override
public boolean isEmpty(){
return array.isEmpty();
}
public int getCapacity(){
return array.getCapacity();
}
@Override
public void enqueue(E e){
array.addLast(e);
}
@Override
public E dequeue(){
return array.removeFirst();
}
@Override
public E getFront(){
return array.getFirst();
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append("Queue: ");
res.append("front [");
for(int i = 0 ; i < array.getSize() ; i ++){
res.append(array.get(i));
if(i != array.getSize() - 1)
res.append(", ");
}
res.append("] tail");
return res.toString();
}
public static void main(String[] args) {
ArrayQueue<Integer> queue = new ArrayQueue<>();
for(int i = 0 ; i < 10 ; i ++){
queue.enqueue(i);
System.out.println(queue);
if(i % 3 == 2){
queue.dequeue();
System.out.println(queue+":================="+(i % 3));
}
}
}
}
2.2.3 执行结果
Queue: front [0] tail
Queue: front [0, 1] tail
Queue: front [0, 1, 2] tail
Queue: front [1, 2] tail:=================2
Queue: front [1, 2, 3] tail
Queue: front [1, 2, 3, 4] tail
Queue: front [1, 2, 3, 4, 5] tail
Queue: front [2, 3, 4, 5] tail:=================2
Queue: front [2, 3, 4, 5, 6] tail
Queue: front [2, 3, 4, 5, 6, 7] tail
Queue: front [2, 3, 4, 5, 6, 7, 8] tail
Queue: front [3, 4, 5, 6, 7, 8] tail:=================2
Queue: front [3, 4, 5, 6, 7, 8, 9] tail
首先我们总共是循环十次,添加到队列中,每天添加一次打印队列中的元素,如果遇到 i % 3 == 2,我们就去除队首的元素,就是我们在结果中看到的 =================2的位置,每次都会把最先添加(队首)的元素给删除掉,从上面的结果中可以看出,当我们每次去 queue.dequeue()元素的时候,其实就是操作数组中的 size --,这样对于我们队列来说效率其实是很慢的,如果删除队首元素,后面的元素就要往前移动,对应的时间复杂度就是O(n)。
2.2.4 数组队列复杂度分析
| 方法 | 时间复杂度 |
|---|---|
| void enqueue(E e) | O(1) 均摊 |
| E dequeue() | O(n) |
| E getFront() | O(1) |
| int getSize() | O(1) |
| boolean isEmpty() | O(1) |
2.2.4 数组队列的问题
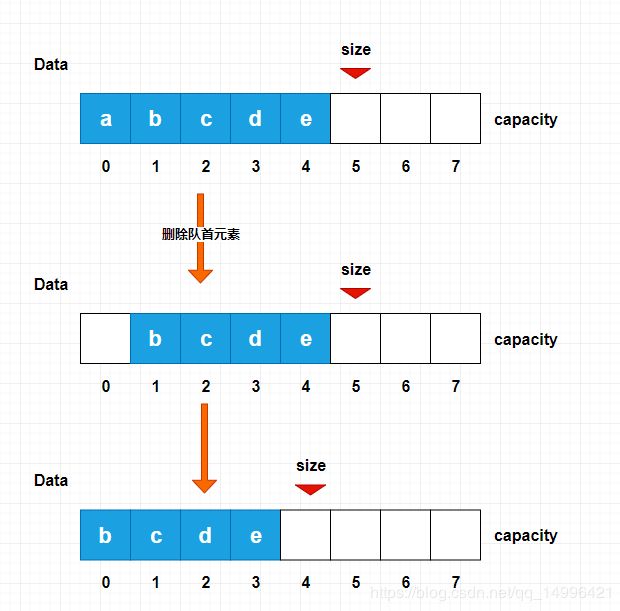
从上面的执行结果我们可以看到,对于队列的执行来说,删除队首元素,后面的元素就要往前移动,如果,有一个n个元素的队列,数组下标 0 的一端是队首,入队操作(void enqueue(E e))就是通过数组下标一个个顺序追加,不需要移动元素,但是如果删除(E dequeue())队首元素,后面的元素就要往前移动,我们可以想象一下,有一个 10000 的元素,我们从下标 0 开始添加,添加完成后,删除 队首的元素,那么我们需要移动 9999 次, 这个操作的复杂度,对于 数组队列来说是非常耗时的一个操作。
2.3 队列的实现(循环队列)
2.3.1 循环队列
每当我们删除队首元素,后面的元素就要往前移动,因为,我们可以使用另一种方式来实现队列,也就是我们上面提到的 链式存储,也称 循环队列,这种方式是使用 链表 实现,比如:有两个指针,front 指向队头,tail 指向对尾元素的下一个位置,元素出队时 front 往后移动,如果到了对尾则转到头部,同理入队时 tail 后移,如果到了对尾则转到头部,这样通过下标 front 出队时,就不需要移动元素了,如果当我们的 front == tail的时候,则说明队列为空。如下图所示:
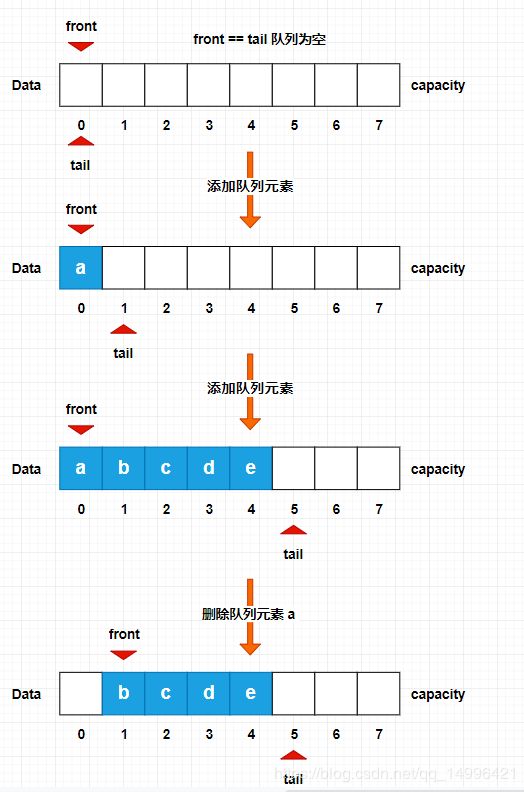
这样我们的删除操作就变成了一个O(1) 的操作,如果当我们的 tail 满了,但是 front 前面还有空间,我们可以将 tail 引入之前在 front 前面删除的下标中 ,这样我们又可以继续添加数据了,这就是循环队列的来由,我们可以把我们的数组队列看成一个 “环”,7 之后的索引是 0 ,什么时候我们的队列才会满呢?当我们的 tail + 1 = front的时候,就说明我们的队列才算真正的满了,如下图所示:
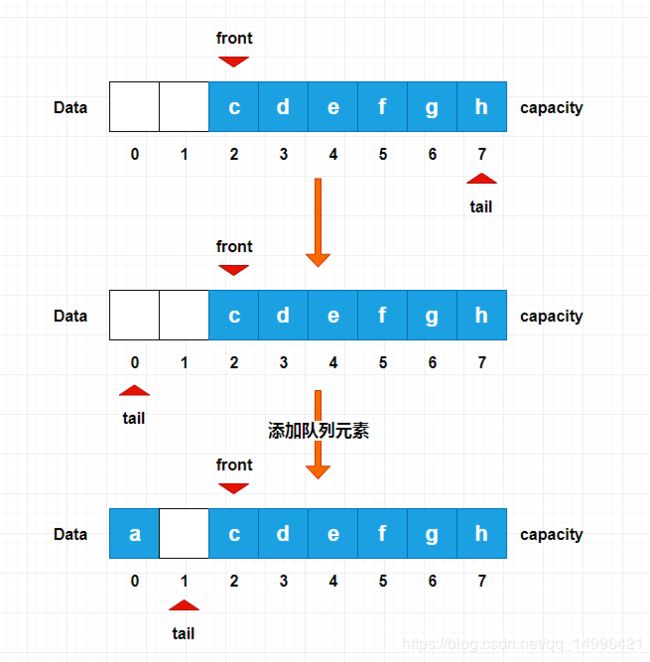
那么,这个时候 front == tail为空 既可以标识为空也可以用于堆满,因此我们可以用 (tail + 1) % c == front的表示队列满了,在这里 c = 8就是我们队列的长度,例如我们的 front 指的是 2 而我们的 tail 指的是 1 的话,那么这个队列就是满的,因为 (1+1)% 8 = 2,大家可以想象一下,我们的钟表,我们的钟表十一点钟下一个时间,我们可以叫12点也可以叫0点,之后又变成了一点两点三点以此类推,我们整个循环队列的就想钟表一样形成了一个环。
注意:在这里我们需要在 capacity 中浪费一个空间,用来判断队列是否满了,因此我们需要在用户传递队列大小的时候,进行 +1 操作,再添加一个元素空间。
2.3.1 循环队列编码实现
首先我们需要以下几个元素:
int getSize(); // 获取队列的元素多少
boolean isEmpty(); //查看队列是否为空
void enqueue(E e); //添加队列元素
E dequeue(); //删除队列队首元素
E getFront(); //获取队首队列元素
1、接口类:
public interface Queue<E> {
int getSize();
boolean isEmpty();
void enqueue(E e);
E dequeue();
E getFront();
}
2、接口实现类:
public class LoopQueue<E> implements Queue<E> {
private E[] data;//存放的元素
private int front, tail;//两个指针
private int size;//元素个数
public LoopQueue(int capacity){
data = (E[])new Object[capacity + 1];//进行 +1 操作,用来判断队列是否满了
front = 0;
tail = 0;
size = 0;
}
public LoopQueue(){
this(10);
}
public int getCapacity(){
return data.length - 1;//获取数据长度,需要在原来的基础上 -1
}
@Override
public boolean isEmpty(){
return front == tail;//判断队列是否满了,只需要判断是否 front == tail
}
@Override
public int getSize(){
return size;
}
@Override
public void enqueue(E e){//添加元素
if((tail + 1) % data.length == front)//如果判断 (tail + 1) % c == front 成立,表示队列满了,自动扩容
resize(getCapacity() * 2);//扩容原来的两倍
data[tail] = e;
tail = (tail + 1) % data.length;
size ++;
}
@Override
public E dequeue(){//删除元素
if(isEmpty())//判断是否为空
throw new IllegalArgumentException("Cannot dequeue from an empty queue.");
E ret = data[front];//获取队首元素
data[front] = null;//设置为null
front = (front + 1) % data.length;//设置新队首的下标位置
size --;//大小 -1
if(size == getCapacity() / 4 && getCapacity() / 2 != 0)//如果长度大小为 getCapacity() / 4 并且 getCapacity() / 2 != 0 的时候,自动缩减
resize(getCapacity() / 2);
return ret;
}
@Override
public E getFront(){//获取队首元素
if(isEmpty())
throw new IllegalArgumentException("Queue is empty.");
return data[front];
}
private void resize(int newCapacity){//扩容操作
E[] newData = (E[])new Object[newCapacity + 1];
for(int i = 0 ; i < size ; i ++)
newData[i] = data[(i + front) % data.length];
data = newData;
front = 0;
tail = size;
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append(String.format("Queue: size = %d , capacity = %d\n", size, getCapacity()));
res.append("front [");
for(int i = front ; i != tail ; i = (i + 1) % data.length){
res.append(data[i]);
if((i + 1) % data.length != tail)
res.append(", ");
}
res.append("] tail");
return res.toString();
}
public static void main(String[] args){
LoopQueue<Integer> queue = new LoopQueue<>(5);
for(int i = 0 ; i < 10 ; i ++){
queue.enqueue(i);
System.out.println(queue);
if(i % 2 == 0){
queue.dequeue();
System.out.println(queue+":================"+i % 2);
}
}
}
}
3、执行结果:
Queue: size = 1 , capacity = 5
front [0] tail
Queue: size = 0 , capacity = 5
front [] tail:================0
Queue: size = 1 , capacity = 5
front [1] tail
Queue: size = 2 , capacity = 5
front [1, 2] tail
Queue: size = 1 , capacity = 2
front [2] tail:================0
Queue: size = 2 , capacity = 2
front [2, 3] tail
Queue: size = 3 , capacity = 4
front [2, 3, 4] tail
Queue: size = 2 , capacity = 4
front [3, 4] tail:================0
Queue: size = 3 , capacity = 4
front [3, 4, 5] tail
Queue: size = 4 , capacity = 4
front [3, 4, 5, 6] tail
Queue: size = 3 , capacity = 4
front [4, 5, 6] tail:================0
Queue: size = 4 , capacity = 4
front [4, 5, 6, 7] tail
Queue: size = 5 , capacity = 8
front [4, 5, 6, 7, 8] tail
Queue: size = 4 , capacity = 8
front [5, 6, 7, 8] tail:================0
Queue: size = 5 , capacity = 8
front [5, 6, 7, 8, 9] tail
Queue:大小个数
capacity:是队列长度,可以看到自动扩容和缩减
front:队首 tail:队尾
2.3.2 循环队列时间复杂度
| 方法 | 时间复杂度 |
|---|---|
| void enqueue(E e) | O(1) 均摊 |
| E dequeue() | O(1) 均摊 |
| E getFront() | O(1) |
| int getSize() | O(1) |
| boolean isEmpty() | O(1) |
2.3 顺序存储和循环队列性能对比
测试代码:
public class Main {
// 测试使用q运行opCount个enqueueu和dequeue操作所需要的时间,单位:秒
private static double testQueue(Queue<Integer> q, int opCount){
long startTime = System.nanoTime();
Random random = new Random();
for(int i = 0 ; i < opCount ; i ++)
q.enqueue(random.nextInt(Integer.MAX_VALUE));
for(int i = 0 ; i < opCount ; i ++)
q.dequeue();
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
int opCount = 100000;
ArrayQueue<Integer> arrayQueue = new ArrayQueue<>();
double time1 = testQueue(arrayQueue, opCount);
System.out.println("ArrayQueue, time: " + time1 + " s");
LoopQueue<Integer> loopQueue = new LoopQueue<>();
double time2 = testQueue(loopQueue, opCount);
System.out.println("LoopQueue, time: " + time2 + " s");
}
}
执行结果:
ArrayQueue, time: 3.552273371 s
LoopQueue, time: 0.011760769 s
我们可以看到 LoopQueue 性能是远远高于 ArrayQueue 的,我们如果把数据加大 ,差异会更加明显,如果是 1000000 的话,我的新电脑是 ArrayQueue:234s,而LoopQueue 依旧是 0.几秒,大家可以自行测试感受下,不过就算是新电脑,在 1000000 数据下,也要等待一会才能执行完成。
到这里栈和队列就讲完了,大家文章中有改进的地方或者有什么不懂的地方,欢迎大家在下面留言,下一篇,我们将讲解数据结构中最重要一个知识点——链表,喜欢的可以关注我,我是牧小农,我喂自己带盐,学习路上你我同行,大家加油!