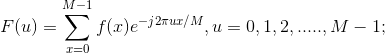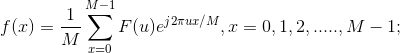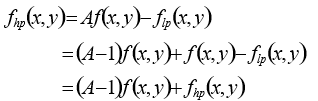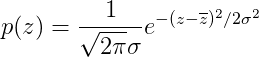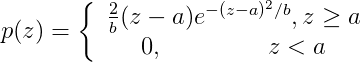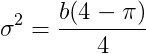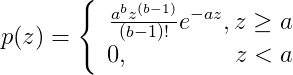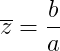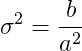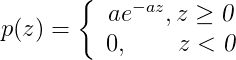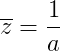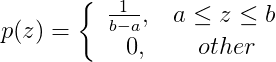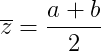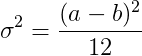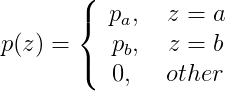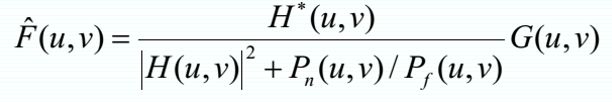数字图像处理简单总结

概念与方法

     一幅图像可定义为一个二维函数f(x,y),其中x,y是空间坐标，而在任何一对空间坐标(x,y)处的幅值称为图像在该点处的强度或灰度。当x,y和灰度值f是有限的离散数值时，我们称该图像为数字图像。
数字图像是由有限的元素组成的，每个元素都有特定的位置和幅值，这些元素称为像素。
数字图像处理是借助于数字计算机来处理数字图像。

采样与量化：所谓的图像数字化，是指将模拟图像经过离散化之后，得到用数字表示的图像。
图像的数字化包括了空间离散化（即采样）和明暗表示数据的离散化（即量化）。

对坐标的数值化称为取样；对幅值的数字化称为量化。

分辨率:  区分图像中的目标物细节的程度，称为图像的分辨率。图像分辨率包括空间分辨力和幅度分辨率，分别由图像的采样和量化决定。

• 空间分辨率是图像中可辨别的最小细节的度量。
• 灰度分辨率是灰度级中可分辨的最小变化。

图像增强: 通过某种技术有选择的突出对某一具体应用有用的信息，削弱或抑制一些无用的信息。

• 基于图像的灰度直方图，根据所在空间不同，分为空域和频域两种。
• 常用的彩色增强有：真彩色增强技术、假彩色增强技术、伪彩色增强技术。

图像加减乘除：相加用于平滑噪声，相减用于增强差别，相乘用于矫正阴影和模板操作。

直方图均衡化：对在图像中像素的个数多的灰度级进行展宽，而对像素个数少的灰度级进行缩减，从而达到清晰图像的目的。

直方图匹配:    直方图规定化是使原图像灰度直方图变成规定形状的直方图而对图像作修正的增强方法，也称为直方图匹配

空域滤波：

• 空域滤波是指利用像素及像素邻域组成的空间进行图像增强的方法。
• 其原理是对图像进行模板运算。
• 模板运算的基本思路是将赋予某个像素的值作为它本身灰度值和其相邻像素灰度值的函数。

微分滤波器模板系数设计：

     roberts交叉梯度算子，prewitt梯度算子,sobel梯度算子。两种模板处理后取绝对值再相加。

     -1  0              -1  -1  -1            -1  -2  -1

      0  1               0   0   0              0   0   0

                           1   1   1              1   2   1

取样定理：

取样定理百度百科

                                             

如果以超过函数最高频率两倍的取样率来获得样本，连续带限函数能完全由其样本集恢复。

 

混淆：

以低于奈奎斯特取样率取样的最终效果是周期重叠，并且不管使用什么样滤波器，都不可能分离出变换的一个单周期。

由函数欠采样导致的后果称为频率混淆即：一个连续函数的高频分量在取样后的函数中用低频修改的过程。

 

一维DFT及IDFT：

;  若f(x,y)为一幅图像，在原点的傅里叶变换等于该图像的平均灰度级。

DFT步骤：

1. 使用paddedsize获得填充参数：PQ = paddedsize（size（f））；%如果输入是彩色图像，必须要灰度化rgb2gray；
2. 对f(x,y)添加必要的零；
3. 得到使用填充的傅里叶变化：F = fft2(f, PQ(1), PQ(2));
4. 生成一个大小为PQ(1)  X  PQ(2) 的滤波函数H，如果该滤波函数已居中，使用前要令H = ifftshift(H)。
5. 将变换乘以滤波函数：G = H.*F;
6. 获得G的傅里叶逆变换的实部：g = real(ifft2(G));
7. 将左上部分的矩形剪切为原来尺寸大小：g = g(1:size(f,1), 1:size(f, 2));

频率域滤波器：

 

 

高频提升，高频加强，钝化模板

高频滤波后的图像，其背景平均强度 减小到接近黑色（因为高通滤波器滤除 了傅里叶变换的零频率成分: F(0,0)=f(x,y)=0）

 解决办法：把原始图像加到过滤后的 结果，如拉普拉斯算子增强，这种处理 称为高频提升过滤

钝化模板(锐化或高通图像)：从一幅图像减去 其自身模糊图像而生成的锐化图像构成。在频率 域，即从图像本身减去低通滤波（模糊）后的图 像而得到高通滤波（锐化）的图像

高频提升过滤：

当A=1,即高通过滤；当A>1,累加图像本身

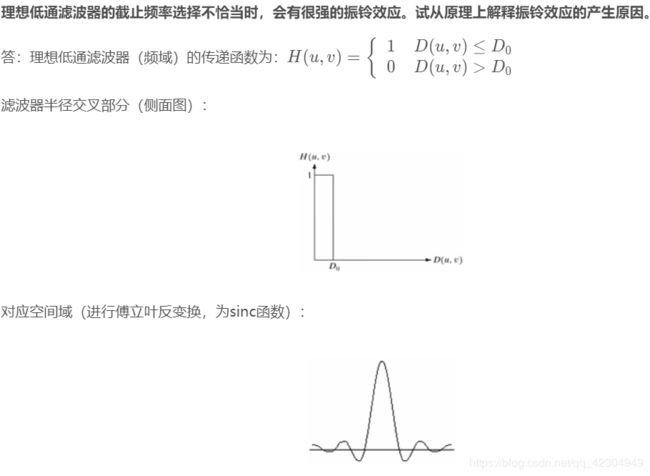
振铃效应

用理想低通滤波器滤波时，频域：G(u,v)=F(u,v)H(u,v)

傅立叶反变换到时域有：g(x,y)=f(x,y)∗h(x,y)

频域相乘相当于时域作卷积。因此，图像经过理想低通滤波器后，时域上相当于原始图像与sinc函数卷积，由于sinc函数振荡，则卷积后图像也会振荡；或者说由于sinc函数有两个负边带，卷积后图像信号两侧出现“过冲现象”，而且能量不集中，即产生振铃效应。若截止频率越低，即D0越小，则sinc函数主瓣越大，表现为中心环越宽，相应周围环（旁瓣）越大。而中心环主要决定模糊，旁瓣主要决定振铃效应。因此当截止频率较低时，会产生很强的振铃效应。选择适当的截止频率，会减小振铃效应

PS:这里的时域也就是空间域

各种噪声概率密度函数

高斯噪声

瑞丽噪声

                          

爱尔兰(伽马)噪声

                                               

指数噪声

                                                             

 

均匀噪声

                                                   

脉冲(椒盐)噪声

图像复原与增强的区别和联系：

• 与图像增强相似，图像复原的目的也是改善图像质量。
• 两者都可以使用空间域或频率域滤波器实现。
• 图像增强主要是一个主观过程，而图像复原主要是一个客观过程。
• 图像增强被认为是一种对比度拉伸，提供给用户喜欢接收的图像;而图像复原技术追求恢复原始图像的最优估值。

 

维纳滤波