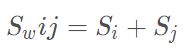人工智能与机器学习——基于Fisher判别的线性分类和对Iris数据集的 Fisher线性分类

一、原理介绍

1. Fisher判别法

Fisher判别法是判别分析的方法之一，它是借助于方差分析的思想，利用已知各总体抽取的样品的p维观察值构造一个或多个线性判别函数y=l′x其中l= (l1，l2…lp)′，x= (x1，x2，…，xp)′，使不同总体之间的离差(记为B)尽可能地大，而同一总体内的离差(记为E)尽可能地小来确定判别系数l=(l1，l2…lp)′。数学上证明判别系数l恰好是|B-λE|=0的特征根，记为λ1≥λ2≥…≥λr>0。所对应的特征向量记为l1，l2，…lr，则可写出多个相应的线性判别函数，在有些问题中，仅用一个λ1对应的特征向量l1所构成线性判别函数y1=l′1x不能很好区分各个总体时，可取λ2对应的特征向量l′2建立第二个线性判别函数y2=l′2x，如还不够，依此类推。有了判别函数，再人为规定一个分类原则(有加权法和不加权法等)就可对新样品x判别所属

2. Fisher线性判别

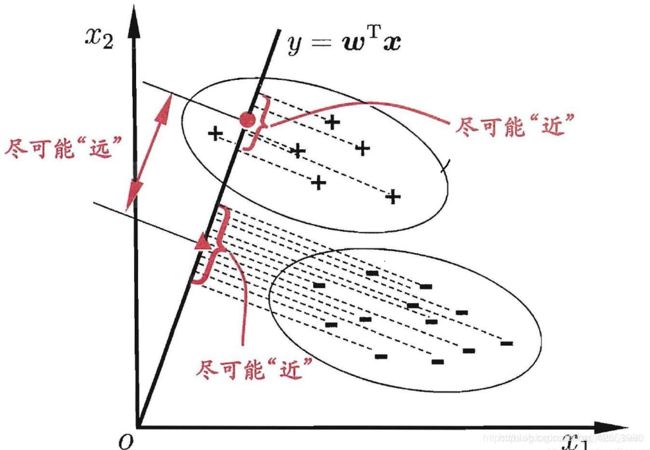
Fisher线性判别分析的基本思想：选择一个投影方向（线性变换，线性组合），将高维问题降低到一维问题来解决，同时变换后的一维数据满足每一类内部的样本尽可能聚集在一起，不同类的样本相隔尽可能地远。
Fisher线性判别分析，就是通过给定的训练数据，确定投影方向W和阈值w0， 即确定线性判别函数，然后根据这个线性判别函数，对测试数据进行测试，得到测试数据的类别。
Fisher判别分析是要实现有最大的类间距离，以及最小的类内距离。

线性判别函数的一般形式可表示成

其中

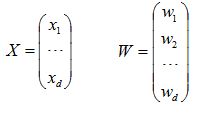
Fisher选择投影方向W的原则，即使原样本向量在该方向上的投影能兼顾类间分布尽可能分开，类内样本投影尽可能密集的要求。

3. “群内离散度”与“群间离散度”

“群内离散度”要求的是距离越远越好；而“群间离散度”的距离越近越好。

“群内离散度”（样本类内离散矩阵）的计算公式为

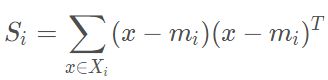
因为每一个样本有多维数据，因此需要将每一维数据代入公式计算后最后在求和即可得到样本类内离散矩阵。存在多个样本，重复该计算公式即可算出每一个样本的类内离散矩阵。

“群间离散度”（总体类离散度矩阵）的计算公式为

二、用python代码实现Fisher判别的推导

#导入包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt 
import seaborn as sns

#导入数据集
df = pd.read_csv("./iris.data", header=0)

Iris1=df.values[0:50,0:4]
Iris2=df.values[50:100,0:4]
Iris3=df.values[100:150,0:4]

#定义类均值向量
m1=np.mean(Iris1,axis=0)
m2=np.mean(Iris2,axis=0)
m3=np.mean(Iris3,axis=0)

#定义类内离散度矩阵
s1=np.zeros((4,4))
s2=np.zeros((4,4))
s3=np.zeros((4,4))
for i in range(0,30,1):
    a=Iris1[i,:]-m1
    a=np.array([a])
    b=a.T
    s1=s1+np.dot(b,a)    
for i in range(0,30,1):
    c=Iris2[i,:]-m2
    c=np.array([c])
    d=c.T
    s2=s2+np.dot(d,c) 
    #s2=s2+np.dot((Iris2[i,:]-m2).T,(Iris2[i,:]-m2))
for i in range(0,30,1):
    a=Iris3[i,:]-m3
    a=np.array([a])
    b=a.T
    s3=s3+np.dot(b,a)
    
#定义总类内离散矩阵
sw12 = s1 + s2;
sw13 = s1 + s3;
sw23 = s2 + s3;

#定义投影方向
a=np.array([m1-m2])
sw12=np.array(sw12,dtype='float')
sw13=np.array(sw13,dtype='float')
sw23=np.array(sw23,dtype='float')
#判别函数以及阈值T（即w0）
a=m1-m2
a=np.array([a])
a=a.T
b=m1-m3
b=np.array([b])
b=b.T
c=m2-m3
c=np.array([c])
c=c.T
w12=(np.dot(np.linalg.inv(sw12),a)).T
w13=(np.dot(np.linalg.inv(sw13),b)).T
w23=(np.dot(np.linalg.inv(sw23),c)).T
T12=-0.5*(np.dot(np.dot((m1+m2),np.linalg.inv(sw12)),a))
T13=-0.5*(np.dot(np.dot((m1+m3),np.linalg.inv(sw13)),b))
T23=-0.5*(np.dot(np.dot((m2+m3),np.linalg.inv(sw23)),c))
#计算正确率
kind1=0
kind2=0
kind3=0
newiris1=[]
newiris2=[]
newiris3=[]
for i in range(30,49):
    x=Iris1[i,:]
    x=np.array([x])
    g12=np.dot(w12,x.T)+T12
    g13=np.dot(w13,x.T)+T13
    g23=np.dot(w23,x.T)+T23
    if g12>0 and g13>0:
        newiris1.extend(x)
        kind1=kind1+1
    elif g12<0 and g23>0:
        newiris2.extend(x)
    elif g13<0 and g23<0 :
        newiris3.extend(x)

for i in range(30,49):
    x=Iris2[i,:]
    x=np.array([x])
    g12=np.dot(w12,x.T)+T12
    g13=np.dot(w13,x.T)+T13
    g23=np.dot(w23,x.T)+T23
    if g12>0 and g13>0:
        newiris1.extend(x)
    elif g12<0 and g23>0:
       
        newiris2.extend(x)
        kind2=kind2+1
    elif g13<0 and g23<0 :
        newiris3.extend(x)
for i in range(30,49):
    x=Iris3[i,:]
    x=np.array([x])
    g12=np.dot(w12,x.T)+T12
    g13=np.dot(w13,x.T)+T13
    g23=np.dot(w23,x.T)+T23
    if g12>0 and g13>0:
        newiris1.extend(x)
    elif g12<0 and g23>0:     
        newiris2.extend(x)
    elif g13<0 and g23<0 :
        newiris3.extend(x)
        kind3=kind3+1
correct=(kind1+kind2+kind3)/60

print('判断出来的综合正确率：',correct*100,'%')

运行结果

三、Iris数据集实战

1. 在命令行下，下载包seaborn

2. 数据可视化

给数据集加上题头

3. relplot

绘制散点图

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
df_Iris = pd.read_csv(r'iris.data.txt')
#sns初始化
sns.set()
#设置散点图x轴与y轴以及data参数
sns.relplot(x='SepalLengthCm', y='SepalWidthCm', data = df_Iris)
plt.title('SepalLengthCm and SepalWidthCm data analysize')

运行结果

（1）. 花萼的长度和宽度在散点图上分了两个簇, 而且两者各自都有一定的关系. 鸢尾花又分为三个品种

#hue表示按照Species对数据进行分类, 而style表示每个类别的标签系列格式不一致.
sns.relplot(x='SepalLengthCm', y='SepalWidthCm', hue='Species', style='Species', data=df_Iris )
plt.title('SepalLengthCm and SepalWidthCm data by Species')

运行结果

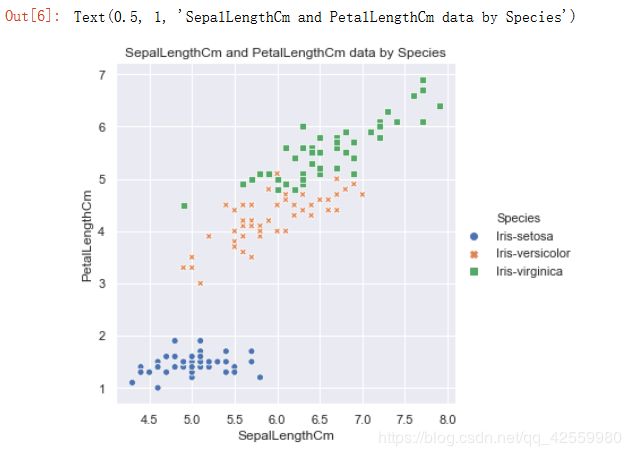
（2）. 对比花萼与花瓣的长度, 花萼与花瓣的宽度之间的关系.

花萼与花瓣长度分布散点图

#花萼与花瓣长度分布散点图
sns.relplot(x='SepalLengthCm', y='PetalLengthCm', hue='Species', style='Species', data=df_Iris )
plt.title('SepalLengthCm and PetalLengthCm data by Species')

运行结果

花萼与花瓣宽度分布散点图

#花萼与花瓣宽度分布散点图
sns.relplot(x='SepalWidthCm', y='PetalWidthCm', hue='Species', style='Species', data=df_Iris )
plt.title('SepalWidthCm and PetalWidthCm data by Species')

运行结果

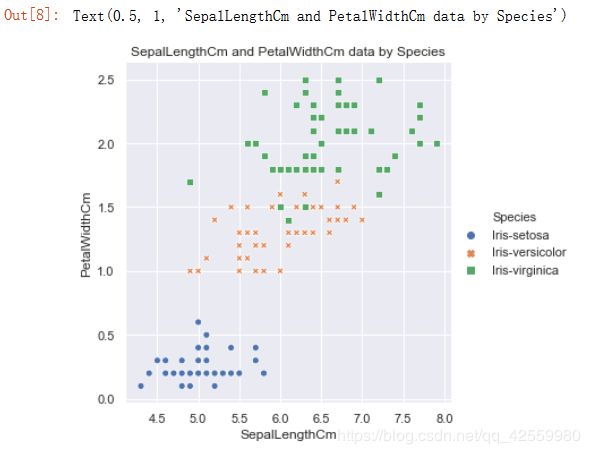
（3）. 花萼的长度与花瓣的宽度, 花萼的宽度与花瓣的长度之间应当也存在某种关系:

花萼的长度与花瓣的宽度分布散点图

#花萼的长度与花瓣的宽度分布散点图
sns.relplot(x='SepalLengthCm', y='PetalWidthCm', hue='Species', style='Species', data=df_Iris )
plt.title('SepalLengthCm and PetalWidthCm data by Species')

运行结果

花萼的宽度与花瓣的长度分布散点图

#花萼的宽度与花瓣的长度分布散点图
sns.relplot(x='SepalWidthCm', y='PetalLengthCm', hue='Species', style='Species', data=df_Iris )
plt.title('SepalWidthCm and PetalLengthCm data by Species') 

运行结果

4. jointplot

绘制散点图和直方图

sns.jointplot(x='SepalLengthCm', y='SepalWidthCm', data=df_Iris)
sns.jointplot(x='PetalLengthCm', y='PetalWidthCm', data=df_Iris)

运行结果


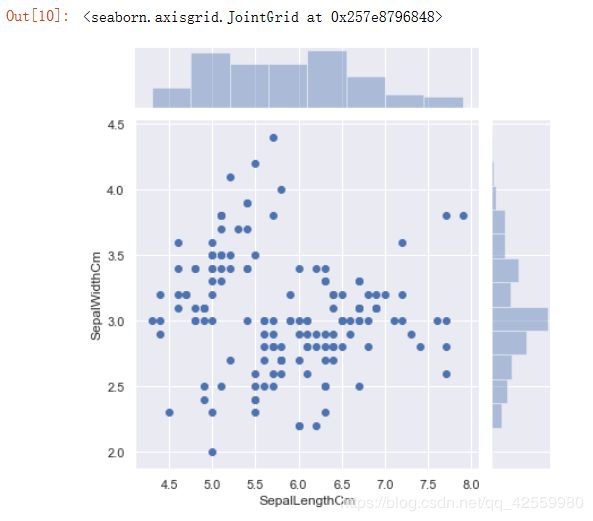
散点图和直方图同时显示, 可以直观地看出哪组频数最大, 哪组频数最小。对于频数的值, 在散点图上数点的话, 显然效率太低, 还易出错，所以我们可以使用distplot

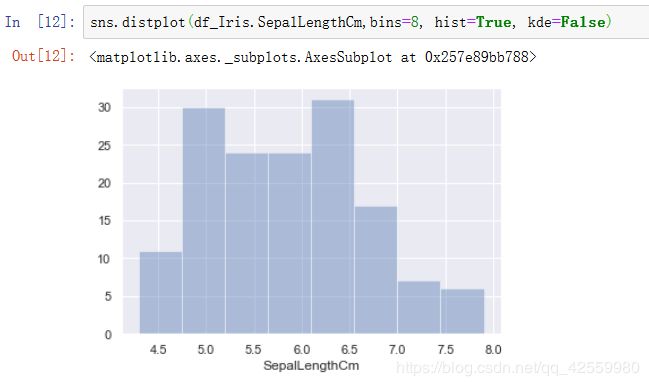
5. distplot

#绘制直方图, 其中kde=False表示不显示核函数估计图,这里为了更方便去查看频数而设置它为False.
sns.distplot(df_Iris.SepalLengthCm,bins=8, hist=True, kde=False)
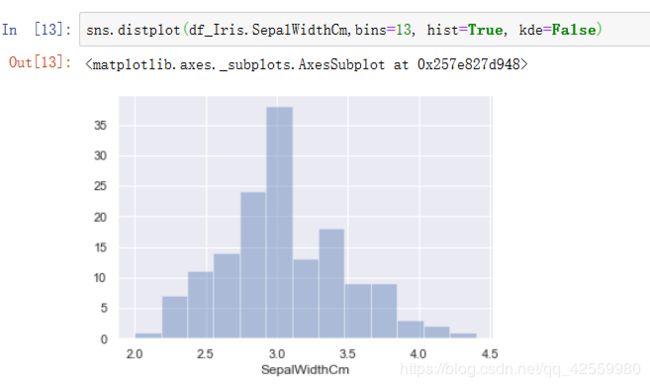
sns.distplot(df_Iris.SepalWidthCm,bins=13, hist=True, kde=False)
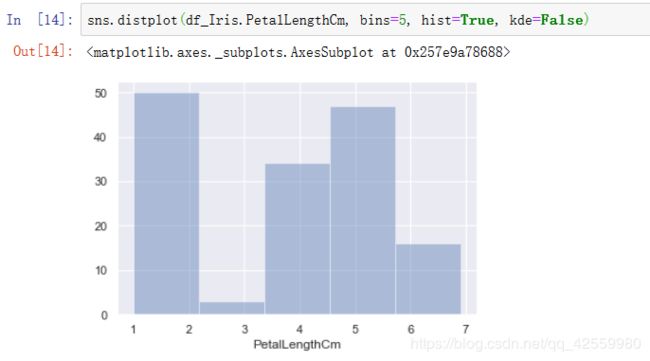
sns.distplot(df_Iris.PetalLengthCm, bins=5, hist=True, kde=False)
sns.distplot(df_Iris.PetalWidthCm, bins=5, hist=True, kde=False)

运行结果

查看每一组的频数

6. boxplot

boxplot所绘制的就是箱线图, 它能显示出一组数据的最大值, 最小值, 四分位数以及异常点。

#比如数据中的SepalLengthCm属性
sns.boxplot(x='SepalLengthCm', data=df_Iris)
#比如数据中的SepalWidthCm属性
sns.boxplot(x='SepalWidthCm', data=df_Iris)

运行结果

将四个属性对应的数值合并在新的DataFrame Iris中.

import numpy as np
#对于每个属性的data创建一个新的DataFrame
Iris1 = pd.DataFrame({"Id": np.arange(1,151), 'Attribute': 'SepalLengthCm', 'Data':df_Iris.SepalLengthCm, 'Species':df_Iris.Species})
Iris2 = pd.DataFrame({"Id": np.arange(151,301), 'Attribute': 'SepalWidthCm', 'Data':df_Iris.SepalWidthCm, 'Species':df_Iris.Species})
Iris3 = pd.DataFrame({"Id": np.arange(301,451), 'Attribute': 'PetalLengthCm', 'Data':df_Iris.PetalLengthCm, 'Species':df_Iris.Species})
Iris4 = pd.DataFrame({"Id": np.arange(451,601), 'Attribute': 'PetalWidthCm', 'Data':df_Iris.PetalWidthCm, 'Species':df_Iris.Species})
#将四个DataFrame合并为一个.
Iris = pd.concat([Iris1, Iris2, Iris3, Iris4])
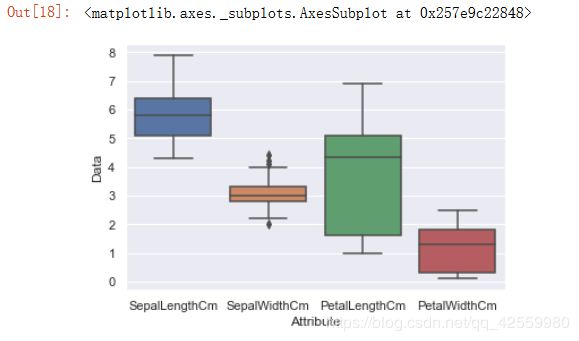
#绘制箱线图
sns.boxplot(x='Attribute', y='Data', data=Iris)

运行结果

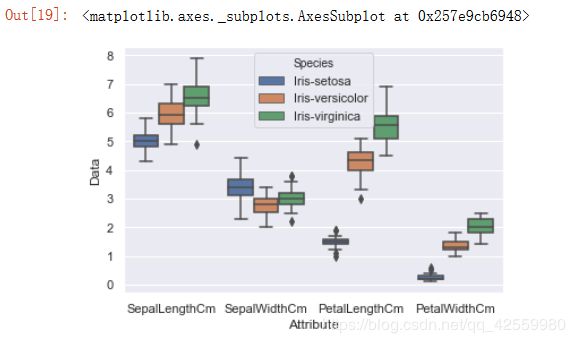
将鸢尾花的三种种类再加入到箱线图中:

sns.boxplot(x='Attribute', y='Data',hue='Species', data=Iris)

运行结果

7. violinplot

violinplot绘制的是琴图, 是箱线图与核密度图的结合体, 既可以展示四分位数, 又可以展示任意位置的密度

sns.violinplot(x='Attribute', y='Data', hue='Species', data=Iris )

运行结果

拆分成四个小图, 为了和箱线图对比, 绘制箱线图

花萼长度

#花萼长度
sns.boxplot(x='Species', y='SepalLengthCm', data=df_Iris)
sns.violinplot(x='Species', y='SepalLengthCm', data=df_Iris)
plt.title('SepalLengthCm data by Species')

运行结果

花萼宽度

#花萼宽度
sns.boxplot(x='Species', y='SepalWidthCm', data=df_Iris)
sns.violinplot(x='Species', y='SepalWidthCm', data=df_Iris)
plt.title('SepalWidthCm data by Species')

运行结果

花瓣长度

#花瓣长度
sns.boxplot(x='Species', y='PetalLengthCm', data=df_Iris)
sns.violinplot(x='Species', y='PetalLengthCm', data=df_Iris)
plt.title('PetalLengthCm data by Species')

运行结果

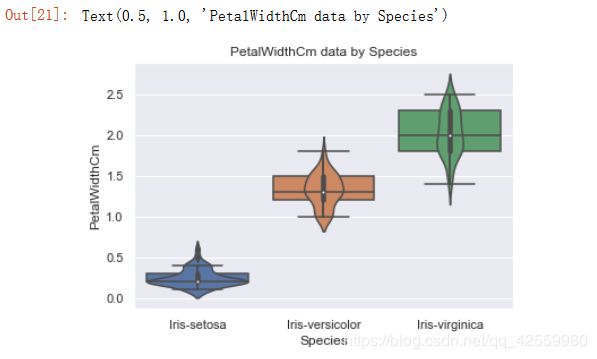
花瓣宽度

#花瓣宽度
sns.boxplot(x='Species', y='PetalWidthCm', data=df_Iris)
sns.violinplot(x='Species', y='PetalWidthCm', data=df_Iris)
plt.title('PetalWidthCm data by Species')

运行结果

琴图中的白点就是中位数, 黑色矩形的上短边则是上四分位数Q3, 黑色下短边则是下四分位数Q1; 而贯穿矩形的黑线的上端点则代表最小非异常值, 下端点则代表最大非异常值; 黑色矩形外部形状则表示核概率密度估计

8. pairplot

能直接显示各个特征之间的不同关系

#绘制分布图
sns.pairplot(df_Iris, hue='Species')
#保存图片, 由于在jupyter notebook中太大, 不能一次截图
plt.savefig('pairplot.png')
plt.show()

运行结果



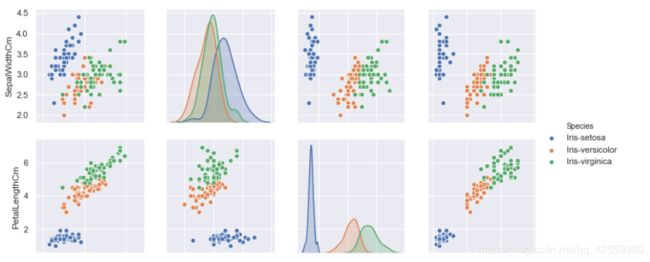
花萼的长度, 花萼的宽度, 花瓣的长度, 花瓣的宽度与花的种类之间均存在一定的相关性, 且对于这三个种类的分布,Iris-satosa在任何一种分布中较其他两者集中; 就同一种花的平均水平来看, 其花萼的长度最长, 花瓣的宽度最短; 就同一属性的平均水平来看, 三种花在除了花萼的宽度外的属性中平均水平均表现为:Iris- Virginica > Iris-versicolour > Iris-setosa.

9. 构建模型

from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier

X = df_Iris[['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm']]
y = df_Iris['Species']
#将数据按照8:2的比例随机分为训练集, 测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
#初始化决策树模型
dt = DecisionTreeClassifier()
#训练模型
dt.fit(X_train, y_train)
#用测试集评估模型的好坏
dt.score(X_test, y_test)

运行结果