非参数统计之局部多项式回归

局部多项式回归

局部多项式回归是非参数回归的一种方法，主要是由于$Nadaraya-Watson$估计方法的加权是基于整个样本点，而且往往在边界上的估计效果并不理想。

局部线性回归

解决上述问题的办法就是用一个变动的函数取代局部固定的权重。局部线性回归就是在待估计点$x$的领域内用一个线性函数$Y_i={\beta }_0+{\beta }_1{X}_i$,$X_i\in [x-h,x+h]$来取代$Y_i$的平均，${\beta }_0,{\beta }_1$是局部参数，首先回顾一下Nadaraya-Watson估计：
$$\begin{array}{rl}{\hat{m}}_h& =\frac{n^{-1}{\sum }_{i=1}^n{K}_h(x-X_i)Y_i}{n^{-1}{\sum }_{j=1}^n{K}_h(x-X_j)}\\ & =\frac{1}{n}\sum _{i=1}^n\left(\frac{K_h(x-X_i)}{n^{-1}{\sum }_{j=1}^n{K}_h(x-X_j)}\right)Y_i\\ & =\frac{1}{n}\sum _{i=1}^n{W}_{hi}(x)Y_i\end{array}$$
其中$K_h(x-X_i)=\frac{1}{h}K\left(\frac{x-X_i}{h}\right)$.接下来我们考虑一个估计量$a\equiv \widehat{m_h}(x)$来使得目标函数(误差平方和)$\frac{1}{2}{\sum }_{i=1}^n(Y_i-a{)}^2$达到最小,很明显它的解是:
$$\begin{array}{rl}\sum _{i=1}^n(Y_i-a)& =0\\ \sum _{i=1}^n{Y}_i& =na\\ a& =\bar{Y}=\widehat{m_h}(x)\end{array}$$
它显然不是$m(x)$的一个好的估计,现在定义权函数$w_i(x)=K((x_i-x)/h)$,再使得下述加权平方和达到最小:
$$\frac{1}{2}\sum _{i=1}^n{w}_i(x)(Y_i-a{)}^2$$
显然它的解是:
$$\widehat{m_h}(x)=\frac{{\sum }_{i=1}^n{w}_i(x)Y_i}{{\sum }_{i=1}^n{w}_i(x)}$$
它刚好就是核回归估计，也说明NW估计是一种由局部加权最小二乘得到的局部常数估计。很明显如果利用线性函数而不是一个常数的话就能得到局部线性回归:
$$\sum _{i=1}^n\{(Y_i-{\beta }_0-{\beta }_1{X}_i){\}}^2{w}_i(x)$$
容易得当不存在$w_i(x)$时上述解为：
$$\{\begin{array}{l}{\beta }_0=\frac{\sum Y_i}{n}-\frac{{\beta }_1\sum X_i}{n}\\ {\beta }_1=\frac{n\sum X_i{Y}_i-\sum X_i{Y}_i}{n\sum X_i^2-\sum X_i\sum X_i}\end{array}$$
当存在$w_i(x)$时上述解为:
$$\{\begin{array}{l}\sum w_i(x)Y_i={\beta }_0\sum w_i(x)+{\beta }_1\sum w_i(x)X_i\\ \sum w_i(x)Y_i{X}_i={\beta }_0\sum w_i(x)X_i+{\beta }_1\sum w_i(x)X_i^2\end{array}$$

局部多项式回归(local polynomial regression)

如果我们把上述中的常数$a$换为一个$p$阶的局部多项式就能得到局部多项式回归.令$x$w为在其上想要估计$m(x)$的某个固定值.则对于在$x$一个邻域中的值$u$，定义多项式
$$P_x(u;a)=a_0+a_1(u-x)+\frac{a_2}{2!}(u-x{)}^2+\cdots +\frac{a_p}{p!}(u-x{)}^p$$
能够在目标值$x$的一个邻域用下面的多项式来近似一个光滑回归函数$m(u)$:
$$m(u)\approx P_x(u;a)$$
有些书籍中的多项式定义为：$m(\cdot )$
$$m(t)\approx m(x)+m^{\prime }(x)(t-x)+\cdots +m^{(p)}(x)(t-x{)}^p\frac{1}{p!}$$
此时的目标函数为:
$$\underset{\beta }{\min }\sum _{i=1}^n\{Y_i-{\beta }_0-{\beta }_1(X_i-x)-\cdots -{\beta }_p(X_i-x{)}^p{\}}^2{K}_h(x-X_i)$$
其中$\beta$表示系数向量$({\beta }_0,{\beta }_1,\dots ,{\beta }_p{)}^{\mathrm{T}}$.
$$X=\left(\begin{array}{ccccc}1& X_1-x& (X_1-x{)}^2& \cdots & (X_1-x{)}^p\\ 1& X_2-x& (X_2-x{)}^2& \cdots & (X_2-x{)}^p\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& X_n-x& (X_n-x{)}^2& \cdots & (X_n-x{)}^p\end{array}\right),Y=\left(\begin{array}{c}{Y}_1\\ Y_2\\ ⋮\\ Y_n\end{array}\right)$$

$$W=\left(\begin{array}{cccc}{K}_h(x-X_1)& 0& \cdots & 0\\ 0& K_h(x-X_2)& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & K_h(x-X_n)\end{array}\right),$$
根据加权最小二乘估计可以得到$\hat{\beta }$:
$$\hat{\beta }(x)=(X^{\mathrm{T}}WX{)}^{-1}{X}^{\mathrm{T}}WY$$
利用上篇文章中的数据举个栗子：

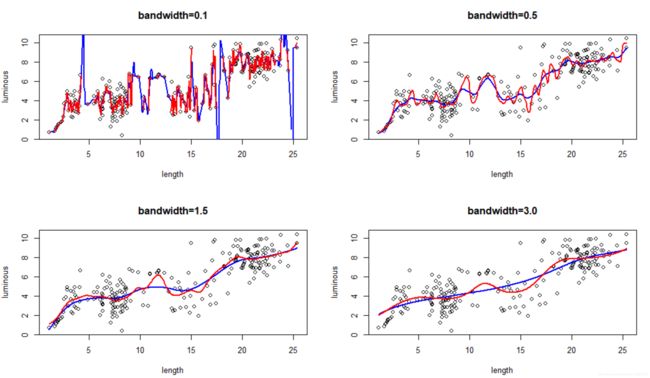
上图中,在相同核函数和窗宽的条件下,红线代表了上篇文章讲到的核回归的结果,蓝线代表了本文中局部多项式回归的结果.可以看到,局部多项式回归的结果更加平缓,极值点处的拟合效果更好.

• R语言代码如下：

par(mfrow=c(2,2))
fit1 <- ksmooth(x=data$length,y=data$luminous,kernel='normal',bandwidth = 0.1,range.x = range(data$length),n.points = length(x))
fit2 <- ksmooth(x=data$length,y=data$luminous,kernel='normal',bandwidth = 0.5,range.x = range(data$length),n.points = length(x))
fit3 <- ksmooth(x=data$length,y=data$luminous,kernel='normal',bandwidth = 1.5,range.x = range(data$length),n.points = length(x))
fit4 <- ksmooth(x=data$length,y=data$luminous,kernel='normal',bandwidth = 3.0,range.x = range(data$length),n.points = length(x))

polyfit <- locpoly(x1,x2,bandwidth = 0.1)
plot(x1,x2,xlab = 'length' ,ylab = 'luminous' ,main='bandwidth=0.1')
lines(polyfit,lwd=2.0,col='blue')
lines(fit1,lwd=2.0,col='red')

polyfit <- locpoly(x1,x2,bandwidth = 0.5)
plot(x1,x2,xlab = 'length' ,ylab = 'luminous' ,main='bandwidth=0.5')
lines(polyfit,lwd=2.0,col='blue')
lines(fit2,lwd=2.0,col='red')


polyfit <- locpoly(x1,x2,bandwidth = 1.5)
plot(x1,x2,xlab = 'length' ,ylab = 'luminous' ,main='bandwidth=1.5')
lines(polyfit,lwd=2.0,col='blue')
lines(fit3,lwd=2.0,col='red')


polyfit <- locpoly(x1,x2,bandwidth = 3.0)
plot(x1,x2,xlab = 'length' ,ylab = 'luminous' ,main='bandwidth=3.0')
lines(polyfit,lwd=2.0,col='blue')
lines(fit4,lwd=2.0,col='red')