gdtop818

Domain-Adversarial Training of Neural Networks

本篇是迁移学习专栏介绍的第十八篇论文，发表在JMLR2016上。

Abstrac

提出了一种新的领域适应表示学习方法，即训练和测试时的数据来自相似但不同的分布。我们的方法直接受到域适应理论的启发，该理论认为，要实现有效的域转移，必须基于不能区分训练(源)域和测试(目标)域的特征进行预测。

该方法在神经网络体系结构的上下文中实现了这一思想，神经网络体系结构的训练对象是源域的标记数据和目标域的未标记数据(不需要标记目标域数据)。随着培训的进展，该方法促进了(i)对源领域的主要学习任务具有任意的特征的出现，(ii)对域之间的转换具有不加区别的特征。

我们证明，这种自适应行为几乎可以在任何前馈模型中实现，通过增加几个标准层和一个新的梯度反转层。生成的增强架构可以使用标准的反向传播和随机梯度下降进行训练，因此可以使用任何深度学习包轻松实现。我们证明了我们的方法成功地解决了两个不同的分类问题(文档情感分析和图像分类)，其中在标准基准上实现了最先进的领域适应性能。我们还验证了描述符学习任务在人员再识别应用中的方法。

1. Introduction

为新的机器学习任务生成标记数据的成本通常是应用机器学习方法的一个障碍。特别是，这是深度神经网络体系结构进一步发展的一个限制因素，深度神经网络体系结构已经在各种机器学习任务和应用中带来了令人印象深刻的最新进展。对于缺少标记数据的问题，仍然有可能获得足够大的训练集来训练大规模的深度模型，但是这些训练集的数据分布与测试时遇到的实际数据发生了变化。一个重要的例子是在合成或半合成图像上训练一个图像分类器，合成或半合成图像可能数量很多，并且被完全标记，但不可避免地具有与真实图像不同的分布(Liebelt and Schmid, 2010; Stark et al., 2010; V´azquez et al., 2014; Sun and Saenko, 2014)。另一个例子是在书面评论的情感分析上下文中，人们可能为一种类型的产品(如电影)的评论标记了数据，同时需要对其他产品(如书籍)的评论进行分类。

在训练分布和测试分布之间存在转移的情况下学习判别分类器或其他预测器被称为域适应(DA)。提出的方法构建源(培训时间)和目标(测试时间)域之间的映射，这样，当使用域之间的学习映射组合时，为源域学习的分类器也可以应用于目标域。域适应方法的吸引力在于，当目标域数据要么完全无标记(无监督域注释)，要么标记样本很少(半监督域适应)时，能够学习域之间的映射。下面，我们将重点讨论更困难的无监督情况，尽管所提出的方法(领域对抗性学习)可以相当直接地推广到半监督情况。

与以往许多使用固定特征表示的领域适应论文不同，我们侧重于将领域适应和深度特征学习结合在一个训练过程中。我们的目标是将领域自适应嵌入到学习表示的过程中，使最终的分类决策基于对领域变化既具有鉴别性又不变性的特征，即，在源和目标域中具有相同或非常相似的分布。这样，得到的前馈网络可以应用于目标域，而不受两个域之间位移的影响。我们的方法是受到领域适应理论的启发(Ben-David et al.， 2006, 2010)，这表明一个好的跨领域转移表示是一个算法无法识别输入观测的原点域。

因此，我们关注结合(i)辨别力和(ii)域不变性的学习特性。这是通过联合优化底层特征以及两种区别的分类器操作这些功能:(i)预测,预测类标签的标签和使用在训练和测试时间,(ii)的域分类器源和目标域之间的歧视在训练。对分类器参数进行优化，使其在训练集上的误差最小;对底层深度特征映射参数进行优化，使标签分类器的损失最小，使域分类器的损失最大。后者因此，update与域分类器相反，它鼓励在优化过程中出现域不变的特性。

至关重要的是,我们表明,所有三个训练过程可以嵌入到一个适当的由深前馈网络,称为domain-adversarial神经网络(丹)(图1所示,第12页),使用标准层和损失函数,可以使用标准的反向传播算法训练基于随机梯度下降法或其修改(例如,SGD动量)。该方法是通用的，因为DANN版本几乎可以为任何可以通过反向传播训练的现有前馈体系结构创建。实际上，所提议的体系结构的唯一非标准组件是一个相当简单的梯度反转层，它在正向传播期间保持输入不变，并在反向传播期间通过将其乘以一个负标量来反转梯度。

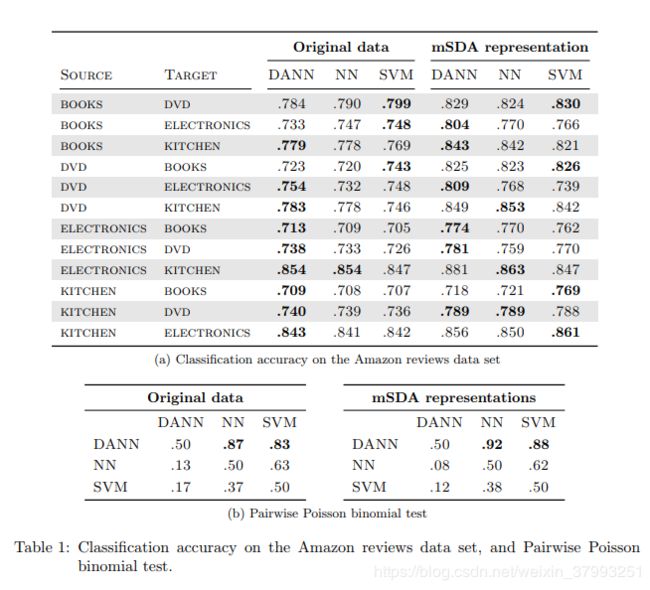
我们提供了一个在一系列深层架构和应用领域的领域对抗学习思想的实验评估。我们首先考虑最简单的DANN体系结构，其中三个部分(标签预测器、领域分类器和特征提取器)是线性的，并证明了这种体系结构的领域对抗学习的成功。对综合数据和自然语言处理中的情绪分析问题进行评估，其中DANN改进了Chen等人(2012)在Amazon review common benchmark上的最先进的边缘化堆叠式自动编码器(mSDA)。

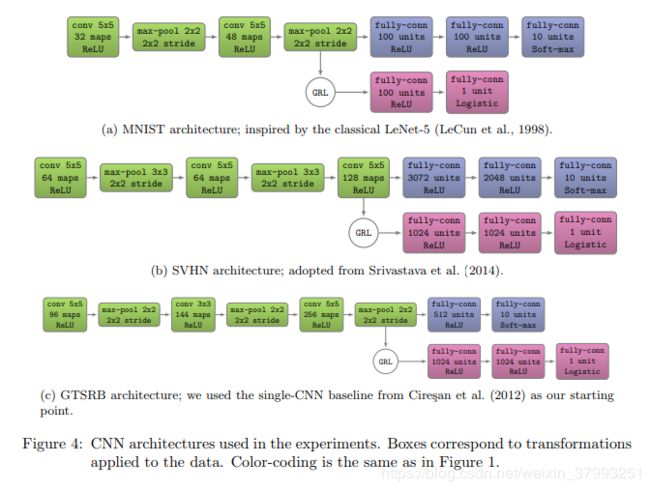
我们进一步评估该方法广泛的图像分类任务,和现在的结果MNIST等传统深度学习图像数据集(勒存et al ., 1998)和SVHN (Netzer et al ., 2011)以及Office benchmarks(Saenko et al ., 2010),在domain-adversarial学习允许获得一个深架构,先进的精度比以往大大提高。

最后，我们评估了领域对抗性描述符学习在人的再识别应用中的应用(Gong et al.， 2014)，其中的任务是获得适合检索和验证的良好的行人图像描述符。我们使用领域对抗性学习，因为我们考虑一个训练有类似暹罗损失的描述符预测器，而不是训练有分类损失的标签预测器。在一系列的实验中，我们证明了域对抗性学习可以显著提高跨数据集的再识别能力。

2. Related work

从许多方面探讨了实现领域适应的一般方法。多年来，大部分文献主要集中在线性假设(Blitzer et al., 2006; Bruzzone and Marconcini, 2010; Germain et al., 2013; Baktashmotlagh et al., 2013; Cortes and Mohri, 2014)。近年来，非线性表征得到了越来越多的研究，包括神经网络表征(Glorot et al., 2011; Li et al., 2014)；最著名的是最先进的mSDA (Chen et al.， 2012)。该文献主要侧重于开发基于去噪自动编码器范式的鲁棒表示原则(Vincent et al.， 2008)。

同时，针对无监督域自适应问题，提出了多种匹配源域和目标域特征分布的方法。一些方法通过从源域重新称重或选择样本来实现这一点(Borgwardt et al., 2006; Huang et al., 2006; Gong et al., 2013)，而其他人则寻求一种明确的特征空间转换，将源分布映射到目标分布(Pan et al., 2011; Gopalan et al., 2011; Baktashmotlagh et al., 2013)。分布匹配方法的一个重要方面是度量分布之间相似性的方法。在这里，一个流行的选择是匹配核再生希尔伯特空间中的分布方式(Borgwardt et al.， 2006;Huang et al.， 2006)，而Gong et al.(2012)和Fernando et al.(2013)绘制了与每个分布相关的主轴。

我们的方法也尝试匹配特征空间分布，但是这是通过修改特征表示本身来实现的，而不是通过重新加权或几何变换。此外，我们的方法使用了一种非常不同的方法来测量分布之间的差异，基于他们的可分性，通过一个深度判别训练分类器。还要注意，有几种方法执行从源到目标域的转换(Gopalan et al., 2011; Gong et al., 2012)通过逐步改变培训分布。在这些方法中，Chopra等人(2013)通过对一系列深度自编码器进行分层训练，逐步用目标域样本替代源域样本，从而进行了深入的研究。与Glorot et al.(2011)的类似方法相比，这一方法得到了改进，Glorot et al.(2011)的方法只是为两个域训练一个单独的深层自动编码器。在这两种方法中，实际的分类器/预测器都是使用自动编码器学习的特征表示在单独的步骤中学习的。与Glorot et al.(2011)相反;Chopra等(2013)，我们的方法在统一的体系结构中，使用单一的学习算法(反向传播)，联合执行特征学习、领域自适应和分类器学习。因此，我们认为我们的方法更简单(无论是在概念上还是在实现上)。我们的方法在流行的Office基准测试上也取得了相当好的结果。

虽然上述方法执行无监督域自适应，但也有一些方法通过利用目标域的标记数据来执行监督域自适应。在深度前馈架构的背景下，这些数据可以用来微调在源域上训练的网络(Zeiler and Fergus, 2013; Oquab et al., 2014; Babenko et al., 2014).。我们的方法不需要标记目标域数据。同时，当这些数据可用时，它可以很容易地合并它们。

Goodfellow等(2014)描述了一个与我们相关的想法。虽然他们的目标是完全不同(建筑生成深层网络,可以合成样品),，他们测量的方式，减少训练数据的分布之间的差异和合成数据的分布非常类似于我们的架构方式措施和最小化两个域之间的差异特征分布。此外，作者提到了饱和乙状结肠的问题，这可能出现在早期的训练阶段，由于领域的显着差异。他们用来回避这个问题的技术(梯度的对抗性部分被相对于适当成本计算的梯度所取代)直接适用于我们的方法。

曾等人(2014)近期及同期报道；Long和Wang(2015)专注于前馈网络中的域适应。他们的技术集度量并最小化跨域的数据分布方式之间的距离(在将分布嵌入RKHS之后，可能会这样做)。因此，他们的方法不同于我们的想法，匹配分布，使他们难以区分的判别分类器。下面，我们将我们的方法与曾等人(2014)进行比较;龙和王(2015)关于办公室基准。Chen et al.(2015)同时开发了另一种深度域适应方法，可以说它与我们的方法更不同。

从理论的角度来看，我们的方法直接来源于Ben-David et al.(2006, 2010)开创性的理论著作。实际上，DANN直接优化了h散度的概念。我们确实注意到了Huang和Yates(2012)的工作，他们使用后验正则化器学习HMM表示来标记单词，后验正则化器也是受到Ben-David等人工作的启发。除了Huang和Yates(2012)的任务不同之外，我们认为DANN learning objective更接近于优化H-divergence, Huang和Yates(2012)出于效率的原因依赖于更为粗糙的逼近。

本文的一部分已作为会议论文发表(Ganin and Lempitsky, 2015)。这个版本扩展了Ganin和Lempitsky(2015)很明显通过合并报告Ajakan et al。(2014)(作为第二个研讨会的一部分转让和多任务学习),这带来了新的术语,深入的理论分析和论证的方法,广泛的实验与浅丹案例对合成数据以及自然语言处理任务(情绪分析)。此外，在这个版本中，我们超越了分类，并对人员重新标识应用程序中的描述符学习设置评估领域对抗性学习。

3. Domain Adaptation

我们考虑分类任务，其中是输入空间， $Y=\{0,1, \ldots, L-1\}$ 是个可能的标签的集合。此外，我们在 $X \times Y$ 上有两种不同的分布，称为源域 $D_{\mathrm{S}}$ 和目标域 $\mathcal{D}_{\mathrm{T}}$ 。然后，给出了一个无监督域自适应学习算法，其中，源样本从 $\mathcal{D}_{\mathrm{S}}$ 绘制i.i.d，目标样本从 $D_{\mathrm{T}}^{\boldsymbol{X}}$ 绘制i.i.d，其中 $D_{\mathrm{T}}^{\boldsymbol{X}}$ 为 $D_{\mathrm{T}}^{\boldsymbol{X}}$ 的边缘分布。

$S=\left\{\left(\mathbf{x}_{i}, y_{i}\right)\right\}_{i=1}^{n} \sim\left(\mathcal{D}_{S}\right)^{n} ; \quad T=\left\{\mathbf{x}_{i}\right\}_{i=n+1}^{N} \sim\left(\mathcal{D}_{\mathrm{T}}^{X}\right)^{n^{\prime}}$

其中 $N=n+n^{\prime}$ 为样本总数。学习算法的目标是建立一个分类器 $\eta : X \rightarrow Y$ 低目标的风险

$R_{\mathcal{D}_{\mathrm{T}}}(\eta)=\operatorname{Pr}_{(\mathbf{x}, y) \sim \mathcal{D}_{\mathrm{T}}}(\eta(\mathbf{x}) \neq y)$

而没有关于 $\mathcal{D}_{\mathrm{T}}$ 标签的信息。

3.1 Domain Divergence

为了解决具有挑战性的领域自适应任务，许多方法通过源误差和源分布与目标分布之间的距离来确定目标误差。通过一个简单的假设，可以直观地证明这些方法是正确的:当两个分布相似时，预期源风险是目标风险的良好指示器。已有几个领域适应的距离概念被提出(Ben-David et al., 2006, 2010; Mansour et al., 2009a,b; Germain et al., 2013)。在本文中，我们主要关注Ben-David等人(2006,2010)使用的H-divergence算法。基于Kifer早期的工作，注意，我们在下面的定义1中假设假设类H是一组(离散的或连续的)二进制分类器 $\eta : X \rightarrow\{0,1\}$

Definition 1 (Ben-David et al., 2006, 2010; Kifer et al., 2004) 给定 $\mathcal{D}_{\mathrm{S}}^{X}$ 和 $D_{\mathrm{T}}^{\boldsymbol{X}}$ 的两个域分布，以及一个假设类H， $\mathcal{D}_{\mathrm{S}}^{X}$ 和 $D_{\mathrm{T}}^{\boldsymbol{X}}$ 的H散度是

$d_{\mathcal{H}}\left(\mathcal{D}_{\mathrm{S}}^{x}, \mathcal{D}_{\mathrm{T}}^{x}\right)=2 \sup _{\eta \in \mathcal{H}} | \operatorname{Pr}_{\mathbf{x} \sim \mathcal{D}_{\mathrm{S}}^{X}}[\eta(\mathbf{x})=1]-\operatorname{Pr}_{\mathbf{x} \sim \mathcal{D}_{\mathrm{T}}}[\eta(\mathbf{x})=1]$

也就是说，H散度依赖于假设类H区分由 $\mathcal{D}_{\mathrm{S}}^{X}$ 生成的例子和由 $D_{\mathrm{T}}^{\boldsymbol{X}}$ 生成的例子的能力。Ben-David等(2006,2010)证明，对于对称假设类H，可以通过计算计算两个样本 $S \sim\left(\mathcal{D}_{\mathrm{S}}^{X}\right)^{n}$ 和 $T \sim\left(\mathcal{D}_{\mathrm{T}}^{X}\right)^{n^{\prime}}$ 之间的经验H散度

$\hat{d_{H}}(S, T)=2\left(1-\min _{\eta \in \mathcal{H}}\left[\frac{1}{n} \sum_{i=1}^{n} I\left[\eta\left(\mathbf{x}_{i}\right)=0\right]+\frac{1}{n^{\prime}} \sum_{i=n+1}^{N} I\left[\eta\left(\mathbf{x}_{i}\right)=1\right]\right)\right)$

其中是指标函数，如果谓词a为真，则为1，否则为0。

3.2 Proxy Distance

Ben-David et al.(2006)提出，即使通常很难精确计算 $\hat{d}_{\mathcal{H}}(S, T)$ (例如，当H是X上线性分类器的空间时)，我们也可以通过对源和目标示例之间的判别问题运行一个学习算法来很容易地逼近它。为此，我们构造一个新的数据集

$U=\left\{\left(\mathbf{x}_{i}, 0\right)\right\}_{i=1}^{n} \cup\left\{\left(\mathbf{x}_{i}, 1\right)\right\}_{i=n+1}^{N}$

其中源样例标记为0，目标样例标记为1。然后，对新数据集进行分类器风险训练U接近 $\varepsilon$ (1)式(1)的“min”部分，给出一个泛化误差在源算例和目标算例的判别问题上，用h -散度近似

$\hat{d}_{\mathcal{A}}=2(1-2 \epsilon)$

在Ben-David等人(2006)中，值 $\hat{d}_{\mathcal{A}}$ 称为代理A-distance (PAD)。A-distance定义为 $d_{A}\left(\mathcal{D}_{\mathrm{S}}^{x}, \mathcal{D}_{\mathrm{T}}^{x}\right)=2 \sup _{A \in \mathcal{A}}\left|\operatorname{Pr}_{\mathcal{D}_{\mathrm{s}}^{\mathrm{x}}(A)-\operatorname{Pr}_{\mathcal{D}_{\mathrm{T}}}^{x}(A) |}\right.$ 其中A是x的子集，注意，通过选择 $\mathcal{A}=\left\{A_{\eta} | \eta \in \mathcal{H}\right\}$ ，与 $A_{\eta}$ 集特征函数所代表的η,定义1的距离和H-divergence是相同的。

在本文的实验部分，我们采用Glorot等(2011)的方法计算PAD值;Chen等(2012)，即,我们训练一个线性支持向量机或更深的MLP分类器对U(公式2)的一个子集,和我们使用分类器获得误差子集在方程(3)的价值。更多的细节和插图的线性支持向量机情况下提供了部分是5.1.5。

3.3 Generalization Bound on the Target Risk

Ben-David et al。(2006年,2010年)也显示,H-divergence $d_{\mathcal{H}}\left(\mathcal{D}_{\mathrm{S}}^{x}, \mathcal{D}_{\mathrm{T}}^{x}\right)$ 上有界的实证估计 $\hat{d}_{\mathcal{H}}(S, T)$ 加上一个常数项取决于复杂性的VC维H和样本大小的S和T .通过结合这个结果与类似的绑定源风险上,下面的定理。

4. Domain-Adversarial Neural Networks （DANN）

我们方法的一个原始方面是将定理2所展示的思想显式地实现为一个神经网络分类器。也就是说，为了学习一个可以很好地从一个领域推广到另一个领域的模型，我们确保神经网络的内部表示不包含关于输入源(源或目标)来源的区别信息，同时在源(标记)示例上保持低风险。

在本节中，我们详细介绍了将领域自适应组件集成到神经网络的方法。在第4.1节中，我们首先对最简单的情况，即，单层隐层，全连通神经网络。然后，我们将描述如何将该方法推广到任意(深度)网络体系结构。

4.1 Example Case with a Shallow Neural Netwo

让我们首先考虑一个标准的神经网络(NN)结构与一个单一的隐藏层。为了简单起见，我们假设输入空间由m维真实向量构成。因此， $X=\mathbb{R}^{m}$ 。隐层Gf学习一个函数 $G_{f} : X \rightarrow \mathbb{R}^{D}$ ，该函数将一个示例映射到一个新的d维表示，并由矩阵-向量对 $(\mathbf{W}, \mathbf{b}) \in \mathbb{R}^{D \times m} \times \mathbb{R}^{D}$ 参数化，

$G_{f}(\mathbf{x} ; \mathbf{W}, \mathbf{b})=\operatorname{sigm}(\mathbf{W} \mathbf{x}+\mathbf{b})$

$\operatorname{sigm}(\mathbf{a})=\left[\frac{1}{1+\exp \left(-a_{i}\right)}\right]_{i=1}^{|\mathbf{a}|}$ 。

这里我们有。通过使用softmax函数，向量 $G_{y}\left(G_{f}(\mathbf{x})\right.$ 的每个分量表示神经网络将x赋值给由该分量表示的Y中的类的条件概率。给定一个源示例 $\left(\mathbf{x}_{i}, y_{i}\right)$ ，使用的自然分类损失是正确labe的负对数概率：

$\mathcal{L}_{y}\left(G_{y}\left(G_{f}\left(\mathbf{x}_{i}\right)\right), y_{i}\right)=\log \frac{1}{G_{y}\left(G_{f}(\mathbf{x})\right)_{y_{i}}}$

然后对神经网络进行训练，在源域上得到如下优化问题

$\min _{\mathbf{w}, \mathbf{b}, \mathbf{V}, \mathbf{c}}\left[\frac{1}{n} \sum_{i=1}^{n} \mathcal{L}_{y}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{V}, \mathbf{c})+\lambda \cdot R(\mathbf{W}, \mathbf{b})\right]$

$\mathcal{L}_{y}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{V}, \mathbf{c})=\mathcal{L}_{y}\left(G_{y}\left(G_{f}\left(\mathbf{x}_{i} ; \mathbf{W}, \mathbf{b}\right) ; \mathbf{V}, \mathbf{c}\right), y_{i}\right)$ 是第i个例子中预测损失的简写符号，R(W, b)是一个可选的正则化器，由超参数加权

·该方法的核心是直接从定义1的h散度出发设计一个域正则化器。为此，我们将隐层Gf(·)(式4)的输出作为神经网络的内部表示。因此，我们表示源样例表示

$S\left(G_{f}\right)=\left\{G_{f}(\mathbf{x}) | \mathbf{x} \in S\right\}$

类似地，给定目标域中的未标记样本，我们表示相应的表示：

$T\left(G_{f}\right)=\left\{G_{f}(\mathbf{x}) | \mathbf{x} \in T\right\}$

根据式(1)，给出了对称假设类H在样本 $S\left(G_{f}\right) \text { and } T\left(G_{f}\right)$ 之间的经验H散度

$\hat{d}_{\mathcal{H}}\left(S\left(G_{f}\right), T\left(G_{f}\right)\right)=2\left(1-\min _{\eta \in \mathcal{H}}\left[\frac{1}{n} \sum_{i=1}^{n} I\left[\eta\left(G_{f}\left(\mathbf{x}_{i}\right)\right)=0\right]+\frac{1}{n^{\prime}} \sum_{i=n+1}^{N} I\left[\eta\left(G_{f}\left(\mathbf{x}_{i}\right)\right)=1\right]\right]\right)$

假设H是表示空间中超平面的一类。灵感来自代理距离(见3.2节),我们建议估算方程(6)的最小部分由域分类层Gd学习物流回归量Gd: RD[0, 1],由一对vector-scalar参数化 $(\mathbf{u}, z) \in \mathbb{R}^{D} \times \mathbb{R}$ ，模型的概率给定输入从源域 $\mathcal{D}_{\mathrm{S}}^{X}$ 或目标域 $D_{\mathrm{T}}^{\boldsymbol{X}}$ 。因此，

$G_{d}\left(G_{f}(\mathbf{x}) ; \mathbf{u}, z\right)=\operatorname{sigm}\left(\mathbf{u}^{\top} G_{f}(\mathbf{x})+z\right)$

因此，函数Gd(·)是一个域回归器。我们定义它的损失b

$\mathcal{L}_{d}\left(G_{d}\left(G_{f}\left(\mathbf{x}_{i}\right)\right), d_{i}\right)=d_{i} \log \frac{1}{G_{d}\left(G_{f}\left(\mathbf{x}_{i}\right)\right)}+\left(1-d_{i}\right) \log \frac{1}{1-G_{d}\left(G_{f}\left(\mathbf{x}_{i}\right)\right)}$

其中di表示第i个示例的二进制变量(域标签)，表示习是来自源分布( $\mathbf{x}_{i} \sim \mathcal{D}_{\mathrm{S}}^{x} \text { if } d_{i}=0$ )还是来自目标分布( $\mathbf{x}_{i} \sim D_{\mathrm{T}}^{x} \text { if } d_{i}=1$ )。回想一下，对于源分布(di=0)中的示例，在训练时已知相应的标签 $y_{i} \in Y$ 。对于来自目标域的示例，我们不知道训练时的标签，我们希望在测试时预测这些标签。这使我们能够向式(5)的目标添加一个域自适应项，给出如下正则化

$R(\mathbf{W}, \mathbf{b})=\max _{\mathbf{u}, z}\left[-\frac{1}{n} \sum_{i=1}^{n} \mathcal{L}_{d}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{u}, z)-\frac{1}{n^{\prime}} \sum_{i=n+1}^{N} \mathcal{L}_{d}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{u}, z)\right]$

$\mathcal{L}_{d}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{u}, z)=\mathcal{L}_{d}\left(G_{d}\left(G_{f}\left(\mathbf{x}_{i} ; \mathbf{W}, \mathbf{b}\right) ; \mathbf{u}, z\right), d_{i}\right)$ 。根据定理2，由式(5)和式(8)给出的优化问题实现了源风险RS(·)最小化与散度dH(·，·)之间的权衡。的hyper-parameterλ用于优化学习过程中这两个量之间的权衡。为了便于学习，我们首先注意到，我们可以将式(5)的完整优化目标重写为

$\begin{aligned} E(\mathbf{W}, \mathbf{V}, \mathbf{b}, \mathbf{c}, \mathbf{u}, z) & \\ &=\frac{1}{n} \sum_{i=1}^{n} \mathcal{L}_{y}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{V}, \mathbf{c})-\lambda\left(\frac{1}{n} \sum_{i=1}^{n} \mathcal{L}_{d}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{u}, z)+\frac{1}{n^{\prime}} \sum_{i=n+1}^{N} \mathcal{L}_{d}^{i}(\mathbf{W}, \mathbf{b}, \mathbf{u}, z)\right) \end{aligned}$

$\begin{aligned}(\hat{\mathbf{W}}, \hat{\mathbf{V}}, \hat{\mathbf{b}}, \hat{\mathbf{c}}) &=\underset{\mathbf{w}, \mathbf{V}, \mathbf{b}, \mathbf{c}}{\operatorname{argmin}} E(\mathbf{W}, \mathbf{V}, \mathbf{b}, \mathbf{c}, \hat{\mathbf{u}}, \hat{z}) \\(\hat{\mathbf{u}}, \hat{z}) &=\underset{\mathbf{u}, z}{\operatorname{argmax}} E(\hat{\mathbf{W}}, \hat{\mathbf{V}}, \hat{\mathbf{b}}, \tilde{\mathbf{c}}, \mathbf{u}, z) \end{aligned}$

4.2 Generalization to Arbitrary Architectures

为了便于说明，到目前为止，我们主要关注单个隐藏层DANN的情况。然而，将其推广到其他复杂的体系结构非常简单，这可能更适合手头的数据。例如，深度卷积神经网络作为学习图像鉴别特征的最先进模型而闻名(Krizhevsky et al.， 2012)。

$\begin{aligned} \mathcal{L}_{y}^{i}\left(\theta_{f}, \theta_{y}\right) &=\mathcal{L}_{y}\left(G_{y}\left(G_{f}\left(\mathbf{x}_{i} ; \theta_{f}\right) ; \theta_{y}\right), y_{i}\right) \\ \mathcal{L}_{d}^{i}\left(\theta_{f}, \theta_{d}\right) &=\mathcal{L}_{d}\left(G_{d}\left(G_{f}\left(\mathbf{x}_{i} ; \theta_{f}\right) ; \theta_{d}\right), d_{i}\right) \end{aligned}$

训练DAAN然后平行于单层的情况，并

$E\left(\theta_{f}, \theta_{y}, \theta_{d}\right)=\frac{1}{n} \sum_{i=1}^{n} \mathcal{L}_{y}^{i}\left(\theta_{f}, \theta_{y}\right)-\lambda\left(\frac{1}{n} \sum_{i=1}^{n} \mathcal{L}_{d}^{i}\left(\theta_{f}, \theta_{d}\right)+\frac{1}{n^{\prime}} \sum_{i=n+1}^{N} \mathcal{L}_{d}^{i}\left(\theta_{f}, \theta_{d}\right)\right)$

$\begin{aligned}\left(\hat{\theta}_{f}, \hat{\theta}_{y}\right) &=\underset{\theta_{f}, \theta_{y}}{\operatorname{argmin}} E\left(\theta_{f}, \theta_{y}, \hat{\theta}_{d}\right) \\ \hat{\theta}_{d} &=\underset{\theta_{d}}{\operatorname{argmax}} E\left(\hat{\theta}_{f}, \hat{\theta}_{y}, \theta_{d}\right) \end{aligned}$

如前所述，由式(11-12)定义的鞍点可以作为后续梯度更新的驻点

$\begin{array}{c}{\theta_{f} \longleftarrow \theta_{f}-\mu\left(\frac{\partial \mathcal{L}_{y}^{i}}{\partial \theta_{f}}-\lambda \frac{\partial \mathcal{L}_{d}^{i}}{\partial \theta_{f}}\right)} \\ {\theta_{y} \longleftarrow \theta_{y}-\mu \frac{\partial \mathcal{L}_{y}^{i}}{\partial \theta_{y}}} \\ {\theta_{d} \longleftarrow \theta_{d}-\mu \lambda \frac{\partial \mathcal{L}_{d}^{i}}{\partial \theta_{d}}}\end{array}$

Domain-Adversarial Training of Neural Networks_第2张图片

图1:提出的体系结构包括一个深特征提取器(绿色)和一个深标签预测器(蓝色)，它们共同构成一个标准的前馈体系结构。在基于反向传播的训练过程中，通过梯度反转层将梯度乘以一定的负常数，将一个域分类器(红色)连接到特征提取器，实现无监督域自适应。否则，训练将按标准进行，并最小化标签预测损失(对于源示例)和域分类损失(对于所有示例)。梯度反转确保了两个域上的特征分布是相似的(对于域分类器来说，尽可能难以区分)，从而产生域不变的特征。

$\begin{array}{l}{\tilde{E}\left(\theta_{f}, \theta_{y}, \theta_{d}\right)=\frac{1}{n} \sum_{i=1}^{n} \mathcal{L}_{y}\left(G_{y}\left(G_{f}\left(\mathbf{x}_{i} ; \theta_{f}\right) ; \theta_{y}\right), y_{i}\right)} \\ {\quad-\lambda\left(\frac{1}{n} \sum_{i=1}^{n} \mathcal{L}_{d}\left(G_{d}\left(\mathcal{R}\left(G_{f}\left(\mathbf{x}_{i} ; \theta_{f}\right)\right) ; \theta_{d}\right), d_{i}\right)+\frac{1}{n^{\prime}} \sum_{i=n+1}^{N} \mathcal{L}_{d}\left(G_{d}\left(\mathcal{R}_{f}\left(\mathbf{x}_{i} ; \theta_{f}\right)\right) ; \theta_{d}\right), d_{i}\right) )}\end{array}$

5. Experiment

你可能感兴趣的:(transfer,learning,Transfer,Learning)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
深度 Qlearning：在直播推荐系统中的应用 AGI通用人工智能之禅程序员提升自我硅基计算碳基计算认知计算生物计算深度学习神经网络大数据 AIGC AGI LLM Java Python 架构设计 Agent 程序员实现财富自由
深度Q-learning：在直播推荐系统中的应用关键词：深度Q-learning,强化学习,直播推荐系统,个性化推荐1.背景介绍1.1问题的由来随着互联网技术的飞速发展,直播平台如雨后春笋般涌现。面对海量的直播内容,用户很难快速找到自己感兴趣的内容。因此,个性化推荐系统在直播平台中扮演着越来越重要的角色。1.2研究现状目前,主流的个性化推荐算法包括协同过滤、基于内容的推荐等。这些方法在一定程度上缓
初识HTTP（1） S1mple_easy 计算机网络学习笔记 http
HTTP基本概念HTTP是超⽂本传输协议，也就是HyperTextTransferProtocol超文本传输协议：HTTP是一个在计算机世界⾥专⻔在两点之间传输⽂字、图⽚、⾳频、视频等超⽂本数据的约定和规范。HTTP常见的状态码具体含义常见状态码1xx提示信息，表示目前是协议处理状态，还需后续操作2xx成功，报文已经收到并被正确处理200/204/2063xx重定向，资源位置发生变动，需要客户端重
云服务业界动态简报-20180128 Captain7
一、青云青云QingCloud推出深度学习平台DeepLearningonQingCloud，包含了主流的深度学习框架及数据科学工具包，通过QingCloudAppCenter一键部署交付，可以让算法工程师和数据科学家快速构建深度学习开发环境，将更多的精力放在模型和算法调优。二、腾讯云1.腾讯云正式发布腾讯专有云TCE(TencentCloudEnterprise)矩阵，涵盖企业版、大数据版、AI
机器学习VS深度学习 nfgo 机器学习
机器学习（MachineLearning,ML）和深度学习（DeepLearning,DL）是人工智能（AI）的两个子领域，它们有许多相似之处，但在技术实现和应用范围上也有显著区别。下面从几个方面对两者进行区分：1.概念层面机器学习：是让计算机通过算法从数据中自动学习和改进的技术。它依赖于手动设计的特征和数学模型来进行学习，常用的模型有决策树、支持向量机、线性回归等。深度学习：是机器学习的一个子领
ResNet的半监督和半弱监督模型 Valar_Morghulis
Billion-scalesemi-supervisedlearningforimageclassificationhttps://arxiv.org/pdf/1905.00546.pdfhttps://github.com/facebookresearch/semi-supervised-ImageNet1K-models/权重在timm中也有：https://hub.fastgit.org/r
联邦学习 Federated learning Google I/O‘19 笔记努力搬砖的星期五笔记联邦学习机器学习机器学习 tensorflow
FederatedLearning:MachineLearningonDecentralizeddatahttps://www.youtube.com/watch?v=89BGjQYA0uE文章目录FederatedLearning:MachineLearningonDecentralizeddata1.DecentralizeddataEdgedevicesGboard:mobilekeyboa
PCL 怎样可视化深度图像 LeonDL168 PCL 计算机视觉人工智能视觉检测图像处理算法
本小节讲解如何可视化深度图像的两种方法，在3D视窗中以点云形式进行可视化（深度图像来源于点云），另一种是，将深度值映射为颜色，从而以彩色图像方式可视化深度图像。代码首先，在PCL（PointCloudLearning）中国协助发行的书提供光盘的第7章例2文件夹中，打开名为range_image_visualization.cpp的代码文件，同文件夹下可以找到相关的测试点云文件room_scan1.
【拖拽】自定义拖拽图标风露_
一、知识点设置被拖拽的元素draggable为true(HTML5新特性)关键方法：voiddataTransfer.setDragImage(img,xOffset,yOffset);注意点：Note:Ifthe[Element]isanexisting[HTMLElement],itneedstobevisibleintheviewportinordertobeshownasadragfeed
TCP实现FTP功能学不会のC tcp/ip linux c语言网络网络协议
文件传输协议（FileTransferProtocol，FTP）是一种在网络中进行文件传输的广泛使用的标准协议。作为网络通信中的基础工具，FTP允许用户通过客户端软件与服务器进行交互，实现文件的上传、下载和其他文件操作。FTP工作在OSI模型的应用层，通常使用TCP作为其传输协议，确保数据传输的可靠性和顺序性。项目要求有服务器和客户端代码，基于TCP写的。在同一路径下，将客户端可执行代码复制到其他
sftp上传和下载文件王小工 Linux linux
SFTP（SSHFileTransferProtocol）是一种基于SSH协议的文件传输协议，它提供了文件传输过程中的加密和验证功能，确保了数据的安全性。SFTP上传和下载文件的过程可以通过多种方式实现，包括使用SFTP客户端软件、命令行工具或编程SDK等。以下是SFTP上传和下载文件的基本步骤和方法：一、SFTP客户端软件操作软件选择与安装：FileZilla：一款广受欢迎的开源FTP客户端，支
http和https区别 m0_73882020 http
HTTP（超文本传输协议）和HTTPS（安全超文本传输协议）是用于在互联网上传输数据的协议。它们之间的主要区别在于安全性：HTTP（HypertextTransferProtocol）:加密:HTTP不对传输的数据进行加密，数据在传输过程中是以明文形式进行的。这意味着任何人都可以在网络中拦截并读取数据。端口:默认使用80端口。适用场景:适用于对安全要求不高的普通网页。HTTPS（Hypertext
Awesome TensorFlow weixin_30594001 人工智能移动开发大数据
AwesomeTensorFlowAcuratedlistofawesomeTensorFlowexperiments,libraries,andprojects.Inspiredbyawesome-machine-learning.WhatisTensorFlow?TensorFlowisanopensourcesoftwarelibraryfornumericalcomputationusin
【ShuQiHere】探索人工智能核心：机器学习的奥秘 ShuQiHere 人工智能机器学习
【ShuQiHere】什么是机器学习？机器学习（MachineLearning,ML）是人工智能（ArtificialIntelligence,AI）中最关键的组成部分之一。它使得计算机不仅能够处理数据，还能从数据中学习，从而做出预测和决策。无论是语音识别、自动驾驶还是推荐系统，背后都依赖于机器学习模型。机器学习与传统的编程不同，它不再依赖于人类编写的固定规则，而是通过数据自我改进模型，从而更灵活
综述论文“A Survey of Zero-Shot Learning: Settings, Methods, and Applications” 硅谷秋水机器学习机器学习神经网络深度学习
该零样本学习综述，发表于ACMTrans.Intell.Syst.Technol.10,2,Article13(January2019)摘要：大多数机器学习方法着重于对已经在训练中看到其类别的实例进行分类。实际上，许多应用程序需要对实例进行分类，而这些实例的类以前没有见过。零样本学习（Zero-ShotLearning）是一种强大而有前途的学习范例，其中训练实例涵盖的类别与想分类的类别是不相交的。
机器学习 VS 表示学习 VS 深度学习 Efred.D 人工智能机器学习深度学习人工智能
文章目录前言一、机器学习是什么?二、表示学习三、深度学习总结前言本文主要阐述机器学习,表示学习和深度学习的原理和区别.一、机器学习是什么?机器学习(machinelearning),是从有限的数据集中学习到一定的规律,再把学到的规律应用到一些相似的样本集中做预测.机器学习的历史可以追溯到20世纪40年代McCulloch提出的人工神经元网络,目前学界大致把机器学习分为传统机器学习和机器学习两个类别
端到端的自动驾驶论文与代码整理大别山伧父自动驾驶
LearningbyCheatinggithubcodearxivpaperconferenceonrobotlearning最新进展(May2021)Checkoutourlatestfollow-upwork:WorldonRails(2020)Checkoutoursubmissiontothe2020CARLAChallenge!pass
妙贼警探第1季第4集中英台词整理和单词统计 littleori
妙贼警探第1季第4集中英台词整理和单词统计英文中文Whatareyouthinking?你在想什么I'mthinkingitwastheaccountant.我想是那个会计Inthelawoffice.律师事务所里的那个Withtheillegalwiretransfer?非法电汇Eitherthat,orcolonelmustardinthelibrary.要么是他要么就是图书馆里的芥末上校[推
Lt-8 Multithreading yanlingyun0210 java
IntendedLearningOutcomesTounderstandtheconceptofconcurrency.Tounderstandthedifferenceofaprocessandathread.TodefineathreadusingtheThreadclassandRunnableinterface.TocontrolthreadswithvariousThreadmethod
如何使用Pytorch-Metric-Learning？鱼儿也有烦恼 PyTorch pytorch
文章目录如何使用Pytorch-Metric-Learning？1.Pytorch-Metric-Learning库9个模块的功能1.1Sampler模块1.2Miner模块1.3Loss模块1.4Reducer模块1.5Distance模块1.6Regularizer模块1.7Trainer模块1.8Tester模块1.9Utils模块2.如何使用PyTorchMetricLearning库中的
NIO笔记03-文件编程齐飞 nio 笔记后端 java
文章目录1FileChannel获取读取写入关闭位置大小强制写入2两个Channel传输数据3Path4Files检查文件是否存在创建一级目录创建多级目录用拷贝文件(和transferTo效率相仿)移动文件删除文件删除目录遍历目录文件拷贝多级目录1FileChannel⚠️FileChannel工作模式：FileChannel只能工作在阻塞模式下获取不能直接打开FileChannel，必须通过Fi
HTTPS和HTTP区别是什么？全真王重阳 #计算机网络 http https 网络协议网络 408 计算机网络
HTTP和HTTPS是两种协议，分别是HyperTextTransferProtocol和HyperTextTransferProtocolSecure。HTTPS还经常被称为HTTPoverSSL或者HTTPoverTSL，HTTPS经由HTTP进行通信，但利用SSL/TLS来加密数据包。他们的区别主要由以下几个方面：安全性:HTTP:HTTP是明文传输的，这意味着数据在传输过程中不加密，容易受
推荐开源项目：PyTorch-Metric-Learning 潘惟妍
推荐开源项目：PyTorch-Metric-Learningpytorch-metric-learningTheeasiestwaytousedeepmetriclearninginyourapplication.Modular,flexible,andextensible.WritteninPyTorch.项目地址:https://gitcode.com/gh_mirrors/py/pytorc
推荐：FastAPI驱动的稳定扩散LLMs演示项目褚知茉Jade
推荐：FastAPI驱动的稳定扩散LLMs演示项目FastAPI-for-Machine-Learning-Live-DemoThisrepositorycontainsthefilestobuildyourveryownAIimagegenerationwebapplication!OutlinedarethecorecomponentsoftheFastAPIwebframework,anda
【python】【Ray的概述】资源存储库 python 开发语言
Overview概述Rayisanopen-sourceunifiedframeworkforscalingAIandPythonapplicationslikemachinelearning.Itprovidesthecomputelayerforparallelprocessingsothatyoudon’tneedtobeadistributedsystemsexpert.Rayminimi
什么是监督学习（Supervised Learning）救救孩子把 AI AI 学习
一、监督学习概述监督学习（SupervisedLearning）是一种极具威力的机器学习方法，能够训练算法以识别数据中的模式，并据此进行精准的预测或分类。借助已有的标记数据，监督学习模型学会了从输入到输出的映射关系，进而在各类实际问题中实现自动化决策。无论是医疗诊断、金融市场分析、客户行为预测，还是提升生产效率以及个性化推荐系统等领域，监督学习都彰显出巨大的潜力与价值。随着技术的持续进步，监督学习
【已解决】如何打开ftp文件合集 moz与京 2024年报错/问题等整理服务器运维计算机网络
别人分享了一个文件夹，说需要的文件就在ftp://xx.xx.x.xxx:xxxx下面的文件目录中，一下子看蒙了。本来以为是常见的链接，但是发现开头是ftp协议。深感困惑，上网搜索以后才知道："FTP（FileTransferProtocol，文件传输协议）是一种用于在计算机网络上进行文件传输的标准协议。它主要用于在客户端和服务器之间传输文件。以下是一些关于FTP协议的关键知识点：1.基本概念：F
使用3DUNet训练自己的数据集（pytorch）— 医疗影像分割编程日记✧ 智能医疗 pytorch 人工智能 python 计算机视觉图像处理深度学习健康医疗
代码：lee-zq/3DUNet-Pytorch:3DUNetimplementedwithpytorch(github.com)文章<cicek16miccai.pdf(uni-freiburg.de)3DU-Net:LearningDenseVolumetricSegmentation
探索任务的隐秘世界：推荐Task2Vec 邓越浪Henry
探索任务的隐秘世界：推荐Task2Vecaws-cv-task2vecOfficialcodeforthepaper"Task2Vec:TaskEmbeddingforMeta-Learning"(https://arxiv.org/abs/1902.03545,ICCV2019)项目地址:https://gitcode.com/gh_mirrors/aw/aws-cv-task2vec在机器学习
论文阅读笔记: DINOv2: Learning Robust Visual Features without Supervision 小夏refresh 论文计算机视觉深度学习论文阅读笔记深度学习计算机视觉人工智能
DINOv2:LearningRobustVisualFeatureswithoutSupervision论文地址:https://arxiv.org/abs/2304.07193代码地址:https://github.com/facebookresearch/dinov2摘要大量数据上的预训练模型在NLP方面取得突破，为计算机视觉中的类似基础模型开辟了道路。这些模型可以通过生成通用视觉特征(即无
java解析APK 3213213333332132 java apk linux 解析APK
解析apk有两种方法 1、结合安卓提供apktool工具，用java执行cmd解析命令获取apk信息 2、利用相关jar包里的集成方法解析apk 这里只给出第二种方法，因为第一种方法在linux服务器下会出现不在控制范围之内的结果。 public class ApkUtil { /** * 日志对象 */ private static Logger
nginx自定义ip访问N种方法 ronin47 nginx 禁止ip访问
　　　因业务需要，禁止一部分内网访问接口，　由于前端架了F5，直接用deny或allow是不行的，这是因为直接获取的前端Ｆ５的地址。　　　所以开始思考有哪些主案可以实现这样的需求，目前可实施的是三种：　　　一：把ip段放在redis里，写一段lua 二：利用geo传递变量，写一段
mysql timestamp类型字段的CURRENT_TIMESTAMP与ON UPDATE CURRENT_TIMESTAMP属性 dcj3sjt126com mysql
timestamp有两个属性，分别是CURRENT_TIMESTAMP 和ON UPDATE CURRENT_TIMESTAMP两种，使用情况分别如下： 1. CURRENT_TIMESTAMP 当要向数据库执行insert操作时，如果有个timestamp字段属性设为 CURRENT_TIMESTAMP，则无论这
struts2+spring+hibernate分页显示 171815164 Hibernate
分页显示一直是web开发中一大烦琐的难题，传统的网页设计只在一个JSP或者ASP页面中书写所有关于数据库操作的代码，那样做分页可能简单一点，但当把网站分层开发后，分页就比较困难了，下面是我做Spring+Hibernate+Struts2项目时设计的分页代码，与大家分享交流。　　1、DAO层接口的设计，在MemberDao接口中定义了如下两个方法： public in
构建自己的Wrapper应用 g21121 rap
我们已经了解Wrapper的目录结构，下面可是正式利用Wrapper来包装我们自己的应用，这里假设Wrapper的安装目录为:/usr/local/wrapper。首先，创建项目应用 &nb
[简单]工作记录_多线程相关 53873039oycg 多线程
最近遇到多线程的问题,原来使用异步请求多个接口(n*3次请求) 方案一使用多线程一次返回数据,最开始是使用5个线程,一个线程顺序请求3个接口,超时终止返回缺点测试发现必须3个接
调试jdk中的源码，查看jdk局部变量程序员是怎么炼成的 jdk 源码
转自：http://www.douban.com/note/211369821/ 学习jdk源码时使用-- 学习java最好的办法就是看jdk源代码，面对浩瀚的jdk（光源码就有40M多，比一个大型网站的源码都多）从何入手呢，要是能单步调试跟进到jdk源码里并且能查看其中的局部变量最好了。可惜的是sun提供的jdk并不能查看运行中的局部变量
Oracle RAC Failover 详解 aijuans oracle
Oracle RAC 同时具备HA(High Availiablity) 和LB(LoadBalance). 而其高可用性的基础就是Failover(故障转移). 它指集群中任何一个节点的故障都不会影响用户的使用，连接到故障节点的用户会被自动转移到健康节点，从用户感受而言，是感觉不到这种切换。 Oracle 10g RAC 的Failover 可以分为3种： 1. Client-Si
form表单提交数据编码方式及tomcat的接受编码方式 antonyup_2006 JavaScript tomcat 浏览器互联网 servlet
原帖地址：http://www.iteye.com/topic/266705 form有2中方法把数据提交给服务器，get和post,分别说下吧。（一）get提交 1.首先说下客户端（浏览器）的form表单用get方法是如何将数据编码后提交给服务器端的吧。对于get方法来说，都是把数据串联在请求的url后面作为参数，如：http://localhost:
JS初学者必知的基础百合不是茶 js函数 js入门基础
JavaScript是网页的交互语言,实现网页的各种效果, JavaScript 是世界上最流行的脚本语言。 JavaScript 是属于 web 的语言，它适用于 PC、笔记本电脑、平板电脑和移动电话。 JavaScript 被设计为向 HTML 页面增加交互性。许多 HTML 开发者都不是程序员，但是 JavaScript 却拥有非常简单的语法。几乎每个人都有能力将小的
iBatis的分页分析与详解 bijian1013 java ibatis
分页是操作数据库型系统常遇到的问题。分页实现方法很多，但效率的差异就很大了。iBatis是通过什么方式来实现这个分页的了。查看它的实现部分，发现返回的PaginatedList实际上是个接口，实现这个接口的是PaginatedDataList类的对象，查看PaginatedDataList类发现，每次翻页的时候最
精通Oracle10编程SQL(15)使用对象类型 bijian1013 oracle 数据库 plsql
/* *使用对象类型 */ --建立和使用简单对象类型 --对象类型包括对象类型规范和对象类型体两部分。 --建立和使用不包含任何方法的对象类型 CREATE OR REPLACE TYPE person_typ1 as OBJECT( name varchar2(10),gender varchar2(4),birthdate date ); drop type p
【Linux命令二】文本处理命令awk bit1129 linux命令
awk是Linux用来进行文本处理的命令，在日常工作中，广泛应用于日志分析。awk是一门解释型编程语言，包含变量，数组，循环控制结构，条件控制结构等。它的语法采用类C语言的语法。 awk命令用来做什么？ 1.awk适用于具有一定结构的文本行，对其中的列进行提取信息 2.awk可以把当前正在处理的文本行提交给Linux的其它命令处理，然后把直接结构返回给awk 3.awk实际工
JAVA(ssh2框架)+Flex实现权限控制方案分析白糖_ java
目前项目使用的是Struts2+Hibernate+Spring的架构模式，目前已经有一套针对SSH2的权限系统，运行良好。但是项目有了新需求：在目前系统的基础上使用Flex逐步取代JSP，在取代JSP过程中可能存在Flex与JSP并存的情况，所以权限系统需要进行修改。【SSH2权限系统的实现机制】权限控制分为页面和后台两块：不同类型用户的帐号分配的访问权限是不同的，用户使
angular.forEach boyitech AngularJS AngularJS API angular.forEach
angular.forEach 描述: 循环对obj对象的每个元素调用iterator, obj对象可以是一个Object或一个Array. Iterator函数调用方法: iterator(value, key, obj), 其中obj是被迭代对象，key是obj的property key或者是数组的index，value就是相应的值啦. (此函数不能够迭代继承的属性.)
java-谷歌面试题-给定一个排序数组，如何构造一个二叉排序树 bylijinnan 二叉排序树
import java.util.LinkedList; public class CreateBSTfromSortedArray { /** * 题目:给定一个排序数组，如何构造一个二叉排序树 * 递归 */ public static void main(String[] args) { int[] data = { 1, 2, 3, 4,
action执行2次 Chen.H JavaScript jsp XHTML css Webwork
xwork 写道 <action name="userTypeAction" class="com.ekangcount.website.system.view.action.UserTypeAction"> <result name="ssss" type="dispatcher">
[时空与能量]逆转时空需要消耗大量能源 comsci 能源
无论如何,人类始终都想摆脱时间和空间的限制....但是受到质量与能量关系的限制,我们人类在目前和今后很长一段时间内,都无法获得大量廉价的能源来进行时空跨越..... 在进行时空穿梭的实验中,消耗超大规模的能源是必然
oracle的正则表达式(regular expression)详细介绍 daizj oracle 正则表达式
正则表达式是很多编程语言中都有的。可惜oracle8i、oracle9i中一直迟迟不肯加入，好在oracle10g中终于增加了期盼已久的正则表达式功能。你可以在oracle10g中使用正则表达式肆意地匹配你想匹配的任何字符串了。正则表达式中常用到的元数据(metacharacter)如下： ^ 匹配字符串的开头位置。 $ 匹配支付传的结尾位置。 *
报表工具与报表性能的关系 datamachine 报表工具 birt 报表性能润乾报表
在选择报表工具时，性能一直是用户关心的指标，但是，报表工具的性能和整个报表系统的性能有多大关系呢？要回答这个问题，首先要分析一下报表的处理过程包含哪些环节，哪些环节容易出现性能瓶颈，如何优化这些环节。一、报表处理的一般过程分析 1、用户选择报表输入参数后，报表引擎会根据报表模板和输入参数来解析报表，并将数据计算和读取请求以SQL的方式发送给数据库。 2、
初一上学期难记忆单词背诵第一课 dcj3sjt126com word english
what 什么 your 你 name 名字 my 我的 am 是 one 一 two 二 three 三 four 四 five 五 class 班级，课 six 六 seven 七 eight 八 nince 九 ten 十 zero 零 how 怎样 old 老的 eleven 十一 twelve 十二 thirteen
我学过和准备学的各种技术 dcj3sjt126com 技术
语言VB https://msdn.microsoft.com/zh-cn/library/2x7h1hfk.aspxJava http://docs.oracle.com/javase/8/C# https://msdn.microsoft.com/library/vstudioPHP http://php.net/manual/en/Html
struts2中token防止重复提交表单蕃薯耀重复提交表单 struts2中token
struts2中token防止重复提交表单 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 蕃薯耀 2015年7月12日 11:52:32 星期日 ht
线性查找二维数组 hao3100590 二维数组
1.算法描述有序（行有序，列有序，且每行从左至右递增，列从上至下递增）二维数组查找，要求复杂度O(n) 2.使用到的相关知识：结构体定义和使用，二维数组传递（http://blog.csdn.net/yzhhmhm/article/details/2045816） 3.使用数组名传递这个的不便之处很明显，一旦确定就是不能设置列值 //使
spring security 3中推荐使用BCrypt算法加密密码 jackyrong Spring Security
spring security 3中推荐使用BCrypt算法加密密码了，以前使用的是md5， Md5PasswordEncoder 和 ShaPasswordEncoder，现在不推荐了，推荐用bcrpt Bcrpt中的salt可以是随机的，比如： int i = 0; while (i < 10) { String password = "1234
学习编程并不难,做到以下几点即可! lampcy java html 编程语言
不论你是想自己设计游戏，还是开发iPhone或安卓手机上的应用，还是仅仅为了娱乐，学习编程语言都是一条必经之路。编程语言种类繁多，用途各异，然而一旦掌握其中之一，其他的也就迎刃而解。作为初学者，你可能要先从Java或HTML开始学，一旦掌握了一门编程语言，你就发挥无穷的想象，开发各种神奇的软件啦。 1、确定目标学习编程语言既充满乐趣，又充满挑战。有些花费多年时间学习一门编程语言的大学生到
架构师之mysql----------------用group+inner join,left join ,right join 查重复数据（替代in) nannan408 right join
1.前言。如题。 2.代码 (1)单表查重复数据,根据a分组 SELECT m.a,m.b, INNER JOIN （select a,b,COUNT(*) AS rank FROM test.`A` A GROUP BY a HAVING rank>1 )k ON m.a=k.a （2）多表查询，使用改为le
jQuery选择器小结 VS 节点查找（附css的一些东西） Everyday都不同 jquery css name选择器追加元素查找节点
最近做前端页面，频繁用到一些jQuery的选择器，所以特意来总结一下：测试页面： <html> <head> <script src="jquery-1.7.2.min.js"></script> <script> /*$(function() { $(documen
关于EXT tntxia ext
ExtJS是一个很不错的Ajax框架，可以用来开发带有华丽外观的富客户端应用，使得我们的b/s应用更加具有活力及生命力。ExtJS是一个用 javascript编写，与后台技术无关的前端ajax框架。因此，可以把ExtJS用在.Net、Java、Php等各种开发语言开发的应用中。 ExtJs最开始基于YUI技术，由开发人员Jack
一个MIT计算机博士对数学的思考 xjnine Math
在过去的一年中，我一直在数学的海洋中游荡，research进展不多，对于数学世界的阅历算是有了一些长进。为什么要深入数学的世界？作为计算机的学生，我没有任何企图要成为一个数学家。我学习数学的目的，是要想爬上巨人的肩膀，希望站在更高的高度，能把我自己研究的东西看得更深广一些。说起来，我在刚来这个学校的时候，并没有预料到我将会有一个深入数学的旅程。我的导师最初希望我去做的题目，是对appe