数字图像处理实验二 图像变换

 

一、实验目的

（1）了解图像变换的意义和手段。

（2）熟悉傅立叶变换的基本性质。

（3）通过实验了解二维频谱的分布特点。

（4）了解余弦变换或Walsh－Hadamard变换

二、实验内容

    任意选择几幅图像，对其进行傅立叶变换，观察图像的频谱特征。

   （1）对图像进行傅里叶变换（包括移位和未移位），观察频谱信号

（2）观察频谱的三维图形

①　移位前：

v 代码：

f=zeros(64,64);

f(15:50,15:50)=1;%输入64*64的黑色图像矩阵

F=fft2(f);%平移前傅立叶变换

F2=fftshift(abs(F));%频谱中心化

x=1:64;y=1:64;

%绘制平移前

figure(1)

subplot(1,3,1),imshow(f);title('平移前原始图像');

subplot(1,3,2),imshow(abs(F));title('图像傅里叶变换');

subplot(1,3,3),imshow(abs(F2));title('图像中心化傅里叶变换');

figure(2)

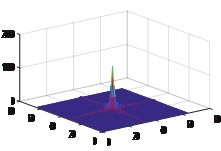
subplot(2,1,1),title('三维图像');

mesh(abs(real(F)),'FaceColor','white');

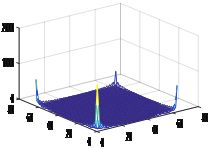
subplot(2,1,2),title('FFT变换');

mesh(x,y,F2(x,y),'FaceColor','red');

结果：

                        图1

                 

图2：彩色三维图像                          图3：FFT变换

②　移位后：

代码：

ff=circshift(f,[-10 -5]);%将原始图像向左向上移，及X轴，Y轴负方向

FF=fft2(ff);%平移后傅立叶变换

FF2=fftshift(abs(FF));%频谱中心化

%绘制平移后

figure(3)

subplot(2,3,1),imshow(ff);title('平移后原始图像');

subplot(2,3,2),imshow(abs(FF));title('图像傅里叶变换');

subplot(2,3,3),imshow(abs(FF2));title('图像中心化傅里叶变换');

figure(4)

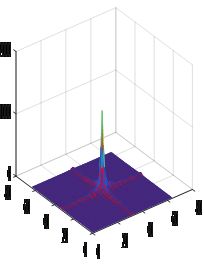
subplot(2,1,1),title('三维图像');

mesh(abs(real(FF)),'FaceColor','white');

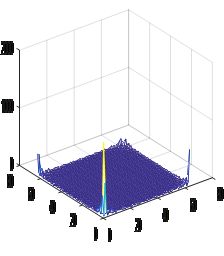
subplot(2,1,2),title('FFT变换');

mesh(x,y,FF2(x,y),'FaceColor','red');

结果：

                      图4

 

                        

  图5：彩色三维图像                            图6：FFT变换

   （3）进行傅里叶逆变换，重建图像

   （4）根据幅值谱重建图像信息

   （5）根据相位谱重建图像信息

代码：

%平移之前的频谱、相位谱、频谱逆变换、相谱逆变换、傅里叶逆变换

xf1=log(abs(F));%频谱

xf2=angle(F);%相位谱

xf12=ifft2(xf1);

xf13=ifftshift(abs(xf12));%频谱逆变换

xf22=ifft2(xf2);

xf23=ifftshift(abs(xf22));%相位逆变换

xr1=ixff1=log(abs(FF));%平移后频谱

%平移之后的频谱、相位谱

xff2=angle(FF);%平移后相位谱

fft2(F);%进行傅里叶逆变换

%平移前平移后相位谱、频谱对比

figure(5)

subplot(2,2,1),imshow(abs(xf2));title('傅里叶相位谱');

subplot(2,2,2),imshow(abs(xff2));title('平移后傅里叶相位谱');

subplot(2,2,3),imshow(abs(xf1));title('傅里叶幅度谱');

subplot(2,2,4),imshow(abs(xff1));title('平移后傅里叶幅度谱');

%平移前逆变换、相位谱逆变换、幅度谱逆变换

figure(6)

subplot(2,2,1),imshow(abs(xf23));title('傅里叶相位谱逆变换');

subplot(2,2,2),imshow(abs(xf13));title('傅里叶幅度谱逆变换');

subplot(2,2,3);imshow(abs(xr1));title('逆变换');

结果：

 

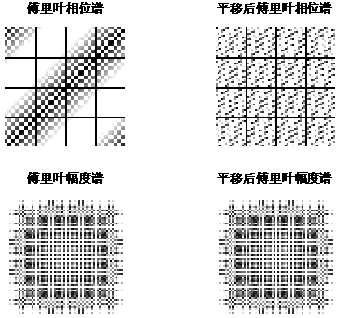
图7：平移前后相位谱、幅度谱

 

图8：平移前逆变换、相位谱逆变换、幅度谱逆变换

 

三、实验分析：

1、图像平移之后的傅里叶幅度谱不会发生变化，而仅仅是相位谱产生了一定的相移特性，如图7

2、图像进行傅里叶变换后，进行傅里叶逆变换会还原为原来的图像，如图8

3、相位谱逆变换之后会大致还原原图像的轮廓、幅度谱逆变换之后还原不出原图像，只会确定图像的精度。如图8

附代码：

f=zeros(64,64);

f(15:50,15:50)=1;%输入64*64的黑色图像矩阵

F=fft2(f);%平移前傅立叶变换

F2=fftshift(abs(F));%频谱中心化

x=1:64;

y=1:64;

 

%平移之前的频谱、相位谱、频谱逆变换、相谱逆变换、傅里叶逆变换

xf1=log(abs(F));%频谱

xf2=angle(F);%相位谱

xf12=ifft2(xf1);

xf13=ifftshift(abs(xf12));%频谱逆变换

xf22=ifft2(xf2);

xf23=ifftshift(abs(xf22));%相位逆变换

xr1=ifft2(F);%进行傅里叶逆变换

 

%平移之后的傅里叶变换频谱、相位谱

ff=circshift(f,[-10 -5]);%将原始图像向左向上移，及X轴，Y轴负方向

FF=fft2(ff);%平移后傅立叶变换

FF2=fftshift(abs(FF));%频谱中心化

xff1=log(abs(FF));%平移后频谱

xff2=angle(FF);%平移后相位谱

 

%绘制平移前

figure(1)

subplot(1,3,1),imshow(f);title('平移前原始图像');

subplot(1,3,2),imshow(abs(F));title('图像傅里叶变换');

subplot(1,3,3),imshow(abs(F2));title('图像中心化傅里叶变换');

 

figure(2)

subplot(2,1,1),title('三维图像');

mesh(abs(real(F)),'FaceColor','white');

subplot(2,1,2),title('FFT变换');

mesh(x,y,F2(x,y),'FaceColor','red');

 

%绘制平移后

figure(3)

subplot(2,3,1),imshow(ff);title('平移后原始图像');

subplot(2,3,2),imshow(abs(FF));title('图像傅里叶变换');

subplot(2,3,3),imshow(abs(FF2));title('图像中心化傅里叶变换');

 

figure(4)

subplot(2,1,1),title('三维图像');

mesh(abs(real(FF)),'FaceColor','white');

subplot(2,1,2),title('FFT变换');

mesh(x,y,FF2(x,y),'FaceColor','red');

 

%平移前平移后相位谱、频谱对比

figure(5)

subplot(2,2,1),imshow(abs(xf2));title('傅里叶相位谱');

subplot(2,2,2),imshow(abs(xff2));title('平移后傅里叶相位谱');

subplot(2,2,3),imshow(abs(xf1));title('傅里叶幅度谱');

subplot(2,2,4),imshow(abs(xff1));title('平移后傅里叶幅度谱');

 

%平移前逆变换、相位谱逆变换、幅度谱逆变换

figure(6)

subplot(2,2,1),imshow(abs(xf23));title('傅里叶相位谱逆变换');

subplot(2,2,2),imshow(abs(xf13));title('傅里叶幅度谱逆变换');

subplot(2,2,3);imshow(abs(xr1));title('逆变换');