Python编程利用单纯形法和scipy库对比分析求解线性规划最大值和最优解问题
Python编程利用单纯形法和scipy库对比分析求解线性规划最大值和最优解问题
- 一、单纯形法介绍
- 1、什么是单纯形法
- 2、单纯形法求解思路
- 3、单纯形法步骤
- 4、最优解可能出现的情况
- 二、具体题目实例
- 三、利用单纯形法求解线性规划最优解和最大值
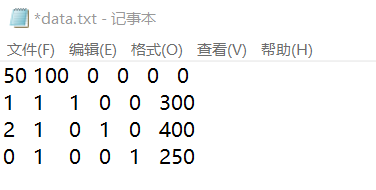
- 1、编写数据文档,填入线性回归分析标准化模型
- 2、编写Python代码
- 四、利用Python中的scipy库对线性规划的最优解、最大值进行求解
- 1、编写Python代码
- 2、运行结果
- 五、两种方法对比分析
一、单纯形法介绍
1、什么是单纯形法
单纯形法 simplex method 求解线性规划问题的通用方法。单纯形是美国数学家G.B.丹齐克于1947年首先提出来的。它的理论根据是:线性规划问题的可行域是 n维向量空间Rn中的多面凸集,其最优值如果存在必在该凸集的某顶点处达到,顶点所对应的可行解称为基本可行解。
2、单纯形法求解思路
先找出一个基本可行解,对它进行鉴别,看是否是最优解;若不是,则按照一定法则转换到另一改进的基本可行解,再鉴别;若仍不是,则再转换,按此重复进行。因基本可行解的个数有限,故经有限次转换必能得出问题的最优解。如果问题无最优解也可用此法判别。 根据单纯形法的原理,在线性规划问题中,决策变量(控制变量)x1,x2,…x n的值称为一个解,满足所有的约束条件的解称为可行解。使目标函数达到最大值(或最小值)的可行解称为最优解。这样,一个最优解能在整个由约束条件所确定的可行区域内使目标函数达到最大值(或最小值),求解线性规划问题的目的就是要找出最优解。
3、单纯形法步骤
(1)把线性规划问题的约束方程组表达成典范型方程组,找出基本可行解作为初始基本可行解。
(2)若基本可行解不存在,即约束条件有矛盾,则问题无解。
(3)若基本可行解存在,从初始基本可行解作为起点,根据最优性条件和可行性条件,引入非基变量 取代某一基变量,找出目标函数值更优的另一基本可行解
(4)按步骤3进行迭代,直到对应检验数满足最优性条件(这时目标函数值不能再改善),即得到问题的 最优解。
(5)若迭代过程中发现问题的目标函数值无界,则终止迭代。
注意:用单纯形法求解线性规划问题所需的迭代次数主要取决于约束条件的个数。现在一般的线性规划问题都是应用单纯形法标准软件在计算机上求解,对于具有106个决策变量和104个约束条件的线性规划问题已能在计算机上解得。
4、最优解可能出现的情况
(1)存在着一个最优解
(2)存在着无穷多个最优解
(3)不存在最优解
注意:不存在最优解只在两种情况下发生,即没有可行解或各项约束条件不阻止目标函数的值无限增大(或向负的方向无限增大)
二、具体题目实例
求解以下约束条件的线性规划的最大值和最优解
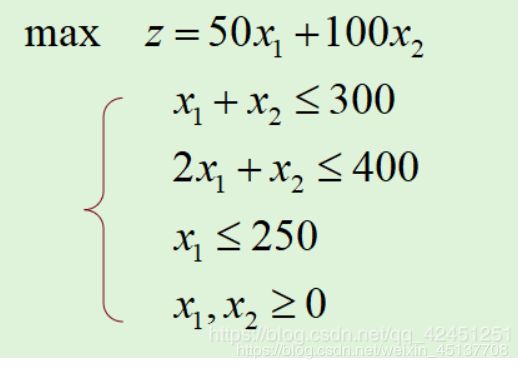
一般解题步骤:
(1)线性规范-标准化:引入松弛变量:s1,s2,s3
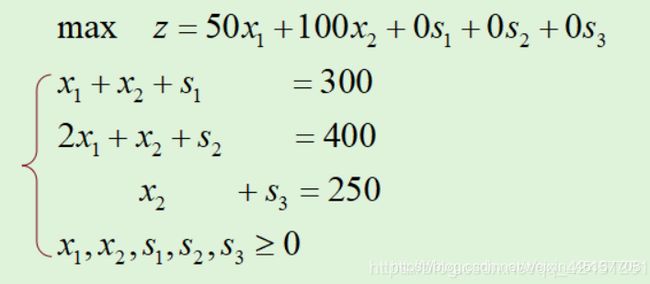
(2)提取系数,填入表格
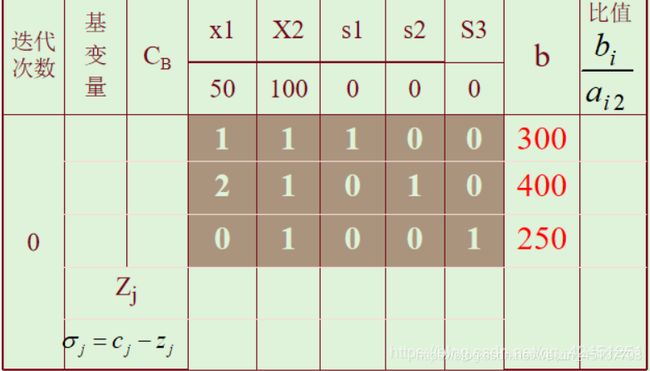
上图区域解答:
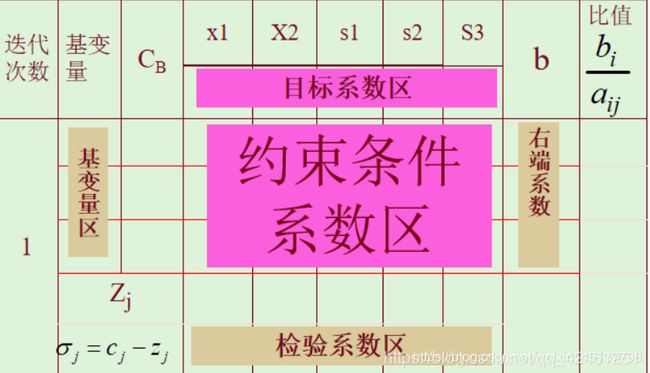
其中,s1、s2、s3作为基:
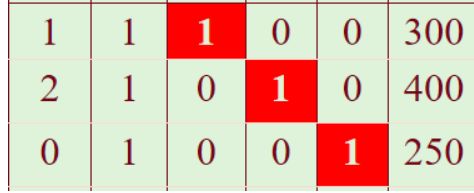
(3)从初始基本可行解X0迭代出另一个基本可行解X1,并判断X1是否为最优解
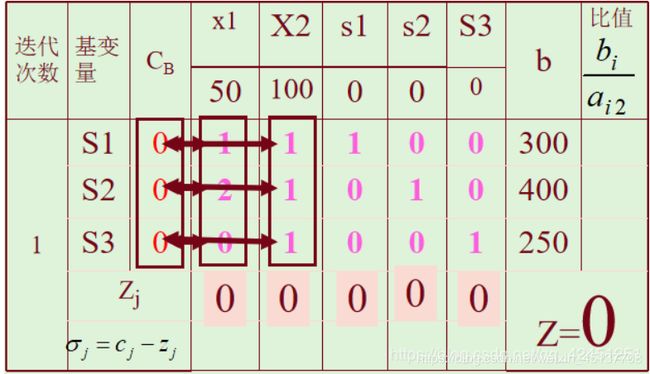
该题最优解为:Z=27500,X1=50,X2=250,S1=50,s2=s3=0
三、利用单纯形法求解线性规划最优解和最大值
1、编写数据文档,填入线性回归分析标准化模型
2、编写Python代码
导入库
import numpy as np
定义列出线性回归系数模型函数
def pivot(d,bn):
l = list(d[0][:-2])
jnum = l.index(max(l)) #转入编号
m = []
for i in range(bn):
if d[i][jnum] == 0:
m.append(0.)
else:
m.append(d[i][-1]/d[i][jnum])
inum = m.index(min([x for x in m[1:] if x!=0])) #转出下标
s[inum-1] = jnum
r = d[inum][jnum]
d[inum] /= r
for i in [x for x in range(bn) if x !=inum]:
r = d[i][jnum]
d[i] -= r * d[inum]
定义更新基变量函数:从一个初始极点出发,不断找到更优的相邻极点,直到找到最优的极点(或极线)
def solve(d,bn):
flag = True
while flag:
if max(list(d[0][:-1])) <= 0: #直至所有系数小于等于0
flag = False
else:
pivot(d,bn)
定义输出打印结果函数
def printSol(d,cn):
for i in range(cn - 1):
if i in s:
print("x"+str(i)+"=%.2f" % d[s.index(i)+1][-1])
else:
print("x"+str(i)+"=0.00")
print("objective is %.2f"%(-d[0][-1]))
导入线性回归模型、调用函数,求解最优解和最优值
d = np.loadtxt("D:\\data.txt", dtype=np.float)
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) #基变量列表
solve(d,bn)
printSol(d,cn)
运行结果
x2、x3、x4对应引入的变量 s1、s2、s3

完整代码如下:
import numpy as np
def pivot(d,bn):
l = list(d[0][:-2])
jnum = l.index(max(l)) #转入编号
m = []
for i in range(bn):
if d[i][jnum] == 0:
m.append(0.)
else:
m.append(d[i][-1]/d[i][jnum])
inum = m.index(min([x for x in m[1:] if x!=0])) #转出下标
s[inum-1] = jnum
r = d[inum][jnum]
d[inum] /= r
for i in [x for x in range(bn) if x !=inum]:
r = d[i][jnum]
d[i] -= r * d[inum]
def solve(d,bn):
flag = True
while flag:
if max(list(d[0][:-1])) <= 0: #直至所有系数小于等于0
flag = False
else:
pivot(d,bn)
def printSol(d,cn):
for i in range(cn - 1):
if i in s:
print("x"+str(i)+"=%.2f" % d[s.index(i)+1][-1])
else:
print("x"+str(i)+"=0.00")
print("objective is %.2f"%(-d[0][-1]))
d = np.loadtxt("D:\\data.txt", dtype=np.float)
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) #基变量列表
solve(d,bn)
printSol(d,cn)
四、利用Python中的scipy库对线性规划的最优解、最大值进行求解
1、编写Python代码
#导入包
from scipy import optimize
import numpy as np
#确定c,A_ub,B_ub
c = np.array([50,100])
A_ub = np.array([[1,1],[2,1],[0,1]])
B_ub = np.array([300,400,250])
#求解
res =optimize.linprog(-c,A_ub,B_ub)
print(res)
代码说明:
c:c指的应该是要求最大值的函数的系数数组
A_ub:A_ub是应该是不等式未知量的系数矩阵,也就是不等式左边
B_ub:B_ub就是不等式的右边了,也就是不等式右边
注意:如果题目中不等式方向不一样,需要添加负号调节方向,使之对应;相应的,系数矩阵的系数也要改变方向,根据自己情况调整
2、运行结果
五、两种方法对比分析
单纯形法结果

利用scipy库结果
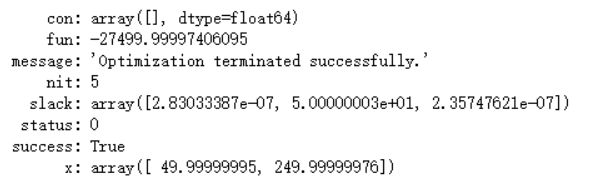
通过以上两种结果对比,不难发现单纯形法的结果更加精确,因为是具体结果x0=50,x1=250;相比于scipy库来说更加精确,从结果来看,不应该是小数,而是整体结果,手工推导也是一样的,相差不大,基本误差在0.00000001左右
参考文献
https://wenku.baidu.com/view/5a9139bb3069a45177232f60ddccda38366be10f.html