leetcode——"树"题目集合
96.不同的二叉搜索树
题目:
给定一个整数 n,求以 1 … n 为节点组成的二叉搜索树有多少种?
示例:
输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
思路:
这其实是一道数学题。假设n个节点组成的二叉树总数为sum[n],而f[n]表示当n为根节点时BST的数目,
所以:
sum[n] = f[1]+f[2]+f[3]…+f[n]
当有n个节点时,i为根节点时,i左边有[1,2,…,i-1]个元素,右边有[i+1,i+2,…n]个元素,所以f[i] = sum[i-1]*sum[n-i],所以:
sum[n] = sum[0] * sum[n-1]+ sum[1] * sum[n-2] + … + sum[n-1] * sum[0]
即:
sum[2] = sum[0]*sum[1]+sum[1]*sum[0];
sum[3] = sum[0]*sum[2]+sum[1]*sum[1]+sum[2]*sum[0]
…
代码:
class Solution {
public int numTrees(int n) {
int[] sum = new int[n+1];
sum[0] = 1;
sum[1] = 1;
//外层计算节点为i的BST总数
for(int i = 2;i <= n;i++){
for(int j = 1;j <= i;j++){
sum[i] += sum[j-1] * sum[i-j];
}
}
return sum[n];
}
}
98. 验证二叉搜索树
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:
2
/ \
1 3
输出: true
示例 2:
输入:
5
/ \
1 4
/ \
3 6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ,但是其右子节点值为 4 。
思路:
中序遍历保持升序即为BST
代码:
1.递归法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
double last = -Double.MAX_VALUE;
public boolean isValidBST(TreeNode root) {
if(root == null) return true;
if(isValidBST(root.left)){
if(last < root.val){
last = root.val;
return isValidBST(root.right);
}
}
return false;
}
}
2.非递归法:
class Solution {
public boolean isValidBST(TreeNode root) {
if(root == null) return true;
Stack stack = new Stack<>();
double last = -Double.MAX_VALUE;
TreeNode cur = root;
while(cur != null || !stack.isEmpty()){
if(cur != null){
stack.push(cur);
cur = cur.left;
}else{
cur = stack.pop();
if(last >= cur.val){
return false;
}
last = cur.val;
cur = cur.right;
}
}
return true;
}
}
99. 恢复二叉搜索树
二叉搜索树中的两个节点被错误地交换。
请在不改变其结构的情况下,恢复这棵树。
示例 1:
输入: [1,3,null,null,2]
1
/
3
\
2
输出: [3,1,null,null,2]
3
/
1
\
2
示例 2:
输入: [3,1,4,null,null,2]
3
/ \
1 4
/
2
输出: [2,1,4,null,null,3]
2
/ \
1 4
/
3
思路:
创建两个集合,通过中序遍历分别储存原先BST的节点值和节点,然后将节点值集合从小到大排序,然后将排好序的值重新按顺序赋给BST节点,即完成规整
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public void recoverTree(TreeNode root) {
//创建两个集合,分别保存原有的TreeNode顺序和TreeNode值
List nodeList = new ArrayList<>();
List valList = new ArrayList<>();
inorder(root,nodeList,valList);
//对原有Tree的值进行排序
Collections.sort(valList);
//然后将排好序的值再放入原有树中
for(int i = 0;i < nodeList.size();i++){
nodeList.get(i).val = valList.get(i);
}
}
public void inorder(TreeNode node,List nodeList,List valList){
if(node == null) return;
inorder(node.left,nodeList,valList);
nodeList.add(node);
valList.add(node.val);
inorder(node.right,nodeList,valList);
}
}
100. 相同的树
给定两个二叉树,编写一个函数来检验它们是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入: 1 1
/ \ / \
2 3 2 3
[1,2,3], [1,2,3]
输出: true
示例 2:
输入: 1 1
/ \
2 2
[1,2], [1,null,2]
输出: false
示例 3:
输入: 1 1
/ \ / \
2 1 1 2
[1,2,1], [1,1,2]
输出: false
思路:
用递归解决:
1.递归结束条件:两个节点都为Null,则返回true
2.如果两个节点都不为null且两个节点的值相等,递归比较两个节点的左节点和两个节点的右节点
3.如果不满足上述情况,则返回false
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p == null && q == null)
return true;
if(p != null && q != null && q.val == p.val){
return isSameTree(p.left,q.left) &&isSameTree(p.right,q.right);
}else{
return false;
}
}
}
101. 对称二叉树
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3
思路:
用递归解决:
1.如果左右节点都为null,则返回true;
2.如果左右节点都部位null且节点值相等,则递归比较左节点的左儿子和右节点的右儿子,以及左节点的右儿子和右节点的左儿子;
3.如果不满足上面的条件,返回false
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null)
return true;
return isMirror(root.left,root.right);
}
public boolean isMirror(TreeNode leftNode,TreeNode rightNode){
if(leftNode == null && rightNode == null)
return true;
if(leftNode != null && rightNode != null && leftNode.val == rightNode.val){
return isMirror(leftNode.left,rightNode.right) && isMirror(leftNode.right,rightNode.left);
}else{
return false;
}
}
}
102. 二叉树的层次遍历
给定一个二叉树,返回其按层次遍历的节点值。 (即逐层地,从左到右访问所有节点)。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[9,20],
[15,7]
]
思路:
使用队列来保存路径,栈中每次保存的是每一层的元素。
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List> levelOrder(TreeNode root) {
List> res = new ArrayList<>();
if(root == null) return res;
Queue queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
//队列中储存的是每一层的节点
int count = queue.size();
//每一次大循环即为一层
List list = new ArrayList<>();
while(count > 0){
TreeNode cur = queue.poll();
count--;
list.add(cur.val);
if(cur.left != null){
queue.add(cur.left);
}
if(cur.right != null){
queue.add(cur.right);
}
}
res.add(list);
}
return res;
}
}
103. 二叉树的锯齿形层次遍历
给定一个二叉树,返回其节点值的锯齿形层次遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回锯齿形层次遍历如下:
[
[3],
[20,9],
[15,7]
]
思路:
和上题的层次遍历一样,只需要设定一个变量作为flag,判断此层结果是否需要翻转即可。
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List> zigzagLevelOrder(TreeNode root) {
List> res = new ArrayList<>();
if(root == null) return res;
Queue queue = new LinkedList<>();
queue.add(root);
boolean flag = false; //是否需要倒序
while(!queue.isEmpty()){
int count = queue.size();
List list = new ArrayList<>();
while(count > 0){
count--;
TreeNode cur = queue.poll();
list.add(cur.val);
if(cur.left != null)
queue.add(cur.left);
if(cur.right != null)
queue.add(cur.right);
}
//如果需要倒序,则将结果翻转
if(flag) Collections.reverse(list);
flag = !flag;
res.add(list);
}
return res;
}
}
104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
思路:
1.递归法:二叉树的最大深度要不就是在左子树上,要不就是在右子树上,两者谁大取谁。
2.层次遍历法:层次遍历,每层次遍历完后深度+1。
代码:
1.递归法:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
if(root == null) return 0;
int a = maxDepth(root.left) + 1;
int b = maxDepth(root.right) + 1;
return Math.max(a,b);
}
}
2.层次遍历法:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
int depth = 0;
if(root == null) return depth;
Queue queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
int count = queue.size();
while(count > 0){
count--;
TreeNode cur = queue.poll();
if(cur.left != null){
queue.add(cur.left);
}
if(cur.right != null){
queue.add(cur.right);
}
}
depth++;
}
return depth;
}
}
105. 从前序与中序遍历序列构造二叉树
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
思路:
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
我们根据前序遍历和后续遍历的结果能得到如下结论:
- 前序遍历结果为【根节点,左子树节点,右子树节点】,数组的第一个元素一定为树的根节点;
- 中序遍历结果为【左子树节点,根节点,右子树节点】,从前序遍历中找出的根节点对应到中序遍历中,索引值为midIndex,左边的值为左子树:[leftInorder,mid-1],右边的值为右子树:[mid+1,rightInorder];
- 因此可以得出左子树的节点个数为:midIndex-leftInorder;
- 右子树节点个数为:rightInorder-midIndex;
- 根据左右子树的个数,可以得到前序遍历中左右子树节点的范围:
- 前序遍历左子树:[leftPre+1,leftPre+midIndex-leftInorder],右子树:[leftPre+1+midIndex-leftInorder+1,rightPre]。
对于这种构建二叉树的题,关键就是递归和区间分治,区间分治的题,采用左闭右闭最为简便,这题我们也采用左闭右闭。
重建二叉树的基本思路就是先构造根节点,再构造左子树,接下来构造右子树,其中,构造左子树和右子树是一个子问题,递归处理即可。因此我们只关心如何构造根节点,以及如何递归构造左子树和右子树。
根节点的值就是前序遍历的第一个值,而根节点的左子树,递归处理得到,前序遍历和中枢遍历数组的区间相应缩小至对应的值,右子树也是一样的,直到数组的起始边界大于终止边界。
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
return build(preorder,0,preorder.length-1,inorder,0,inorder.length-1);
}
public TreeNode build(int[] preorder,int start1,int end1,int[] inorder,int start2,int end2){
if(start1 > end1 || start2 > end2) return null;
TreeNode root = new TreeNode(preorder[start1]);
//找到中序遍历中根元素对应的index
int mid = -1;
for(int i = start2;i <= end2;i++){
if(inorder[i] == preorder[start1])
mid = i;
}
//左子树
root.left = build(preorder,start1+1,start1+mid-start2,inorder,start2,mid-1);
root.right = build(preorder,start1+mid-start2+1,end1,inorder,mid+1,end2);
return root;
}
}
106. 从中序与后序遍历序列构造二叉树
根据一棵树的中序遍历与后序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
思路:
这题的思路和上一题的思路是类似的。
后序遍历的最后一个元素即为根元素,在中序遍历数组中找到对应的索引mid,中序遍历的左子树范围为:[leftInorder,mid-1],右子树范围为:[mid+1,rightInorder],左子树元素个数为:mid-leftInorder,右子树元素个数为:rightInorder-mid。则后续遍历的左子树范围为:[leftPost,leftPost+mid-leftInorder-1],右子树范围为:[leftPost+mid-leftInorder,rightPost-1]。
递归处理即可
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
return build(postorder,0, postorder.length-1,inorder,0, inorder.length-1);
}
public TreeNode build(int[] postorder,int lo1,int hi1,int[] inorder,int lo2,int hi2){
if(lo1 > hi1 || lo2 > hi2) return null;
TreeNode root = new TreeNode(postorder[hi1]);
int mid = -1;
//查找在中序遍历中的index
for(int i = 0;i < inorder.length;i++){
if(inorder[i] == postorder[hi1])
mid = i;
}
//左子树长为mid-lo2
root.left = build(postorder,lo1,lo1+mid-lo2-1,inorder,lo2,lo2+mid-lo2-1);
root.right = build(postorder,lo1+mid-lo2,hi1-1,inorder,mid+1,hi2);
return root;
}
}
107. 二叉树的层次遍历 II
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其自底向上的层次遍历为:
[
[15,7],
[9,20],
[3]
]
思路:
使用栈记录遍历的路径,最后将结果反转即可。
具体看题102.
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List> levelOrderBottom(TreeNode root) {
List> res = new ArrayList<>();
if(root == null) return res;
Queue queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
int count = queue.size();
List list = new ArrayList<>();
while(count > 0){
count--;
TreeNode cur = queue.poll();
list.add(cur.val);
if(cur.left != null){
queue.add(cur.left);
}
if(cur.right != null){
queue.add(cur.right);
}
}
res.add(list);
}
Collections.reverse(res);
return res;
}
}
108. 将有序数组转换为二叉搜索树
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
给定有序数组: [-10,-3,0,5,9],
一个可能的答案是:[0,-3,9,-10,null,5],它可以表示下面这个高度平衡二叉搜索树:
0
/ \
-3 9
/ /
-10 5
思路:
如果只提供了中序遍历,可以构成多个BST,如上述例子中也可以构成如下BST:
0
/ \
-10 9
\ \
-3 5
中序遍历的元素为:【左子树节点,根节点,右子树节点】,所以可以通过求中间索引mid构建根节点,根节点的左子树递归处理,传入左子树的对应数组索引范围,右子树相同处理。
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
//中序遍历的结果反推回树
if(nums.length == 0) return null;
if(nums.length == 1) return new TreeNode(nums[0]);
//根节点是数组中中心元素,左边为左子树,右边为右子树
return getBST(nums,0,nums.length-1);
}
public TreeNode getBST(int[] nums,int lo,int hi){
if(lo > hi) return null;
int mid = lo + ((hi - lo)>>1); //这里右移一位是除以2的优化,因为运算符优先级的关系,要加括号
TreeNode root = new TreeNode(nums[mid]);
root.left = getBST(nums,lo,mid-1);
root.right = getBST(nums,mid+1,hi);
return root;
}
}
110. 平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
1
/ \
2 2
/ \
3 3
/ \
4 4
返回 false 。
思路:
这个题目的关键就是求出当前节点的左子树和右子树的高度差,如果差大于1,则返回false,否则递归求出左右子节点的子树高度差。
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isBalanced(TreeNode root) {
if(root == null) return true;
int left = getHeight(root.left);
int right = getHeight(root.right);
if(Math.abs(left-right) > 1)
return false;
else{
return isBalanced(root.left) && isBalanced(root.right);
}
}
private int getHeight(TreeNode root){
if(root == null) return 0;
return Math.max(getHeight(root.left),getHeight(root.right)) + 1;
}
}
111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最小深度 2.
思路:
这个题目的用例有一个坑,就是当树结构为如下时:
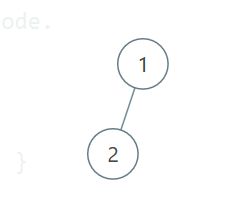
返回值是2,因为题目给出的要求是:最小深度是从根节点到最近叶子节点的最短路径上的节点数量,叶子节点是左右节点为Null的节点。
1.层序遍历法
层序遍历当前树,如果遍历到某个节点的左右节点为Null,则返回当前高度。
2.递归法
递归求出当前节点的左子树高和右子树高度,如果有高度为0,则表示那边的节点不满足叶子节点,则最小深度为另一边高度,如果两边高度都不为0,则就最小值。
代码:
1.层序遍历法:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int minDepth(TreeNode root) {
if(root == null) return 0;
int depth = 1;
Queue queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
int count = queue.size();
while(count > 0){
count--;
TreeNode cur = queue.poll();
if(cur.left == null && cur.right == null)
return depth;
if(cur.left != null)
queue.add(cur.left);
if(cur.right != null)
queue.add(cur.right);
}
depth++;
}
return depth;
}
}
2.递归法:
class Solution {
public int minDepth(TreeNode root) {
if(root == null) return 0;
int a = minDepth(root.left);
int b = minDepth(root.right);
return (a == 0 || b == 0)?a+b+1:Math.min(a,b)+1;
}
}
112. 路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
思路:
因为题目给出的路径是根节点到叶子节点,所以递归结束的条件很好选定,即判断当前节点是否是叶子节点且该节点的值是否为sum,如果是则返回true,如果不是则继续递归其左右子叶,注意递归时sum值需要减去当前节点的值。
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean hasPathSum(TreeNode root, int sum) {
if(root == null) return false;
if(root.left == null && root.right == null && root.val == sum)
return true;
return hasPathSum(root.left,sum-root.val) || hasPathSum(root.right,sum-root.val);
}
}
113. 路径总和 II
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
[
[5,4,11,2],
[5,8,4,5]
]
思路:
递归思路和上题是一致的,只需要添加两个List分别来记录路径和最短路径集合。
有两点需要注意:
1.当路径满足最短路径时,应该添加此时此刻列表的快照,不能直接添加,因为后面还会更改这个列表
2.添加完后不能直接返回,还需要查找其他路径
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
List> res = new ArrayList<>();
List list = new ArrayList<>();
public List> pathSum(TreeNode root, int sum) {
if(root == null) return res;
list.add(root.val);
if(root.left == null && root.right == null && root.val == sum){
res.add(new ArrayList(list));//这里应该添加此时此刻列表的快照,不能直接添加,因为后面还会更改这个列表
//不能直接返回,还需要查找其他路径
}
pathSum(root.left,sum-root.val);
pathSum(root.right,sum-root.val);
list.remove(list.size()-1);
return res;
}
}
116. 填充每个节点的下一个右侧节点指针
给定一个完美二叉树,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例:
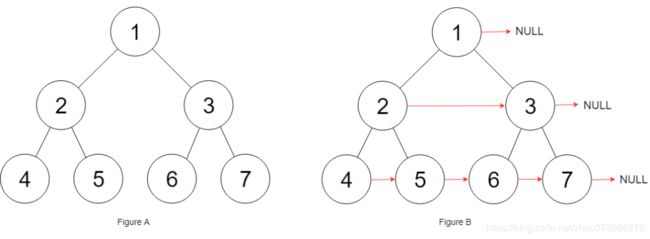 思路:
思路:
1.层序遍历:
这题最直观的解法就是进行层序遍历,每层节点的next节点是下一个节点,最后一个节点的next节点是null。
2.递归法:
因为题目给出的是完美二叉树,即每层的二叉树是满的,不存在缺少的情况,所以对于当前节点:
a.其左子节点的next节点为其右节点
b.其右子节点的next节点为父节点的next节点的左子节点
然后递归处理节点的左子树和右子树即可
代码:
1.层序遍历法
class Solution {
public Node connect(Node root) {
//层序遍历
if(root == null) return null;
Queue queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
int count = queue.size();
while(count > 0){
count--;
Node cur = queue.poll();
//判断是否是最右节点
if(count == 0){
cur.next = null;
}else{
cur.next = queue.peek();
}
//加入下一层
if(cur.left != null){
queue.add(cur.left);
}
if(cur.right != null){
queue.add(cur.right);
}
}
}
return root;
}
}
2.递归法
class Solution {
public Node connect(Node root) {
if(root == null) return null;
//处理左子节点
if(root.left != null && root.right != null){
root.left.next = root.right;
}
//处理右子节点
if(root.next != null && root.right != null && root.next.left != null){
root.right.next = root.next.left;
}
connect(root.left);
connect(root.right);
return root;
}
}
117. 填充每个节点的下一个右侧节点指针 II
给定一个二叉树
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例:
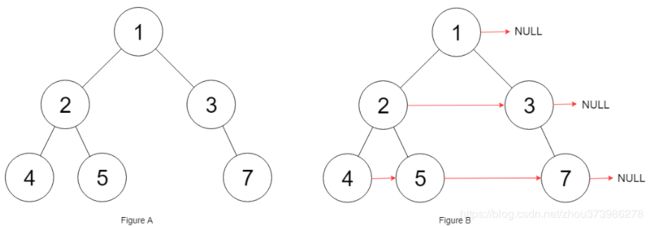 思路:
思路:
和上题不同的是,这里的树是普通树,所以递归处理该题时需要考虑其他情况。当然上题的层序遍历还是可以处理这种情况的。
递归法:
对于左子节点,其next节点有两种情况:
1.如果其右子节点不为null,则左子节点的next节点为右子节点
2.否则,左子节点的next节点为该层离左子节点最近的节点
注意:因为左子节点的next节点的构建依赖于右子树,所以优先递归右子树,等右子树连接完成后再处理左子树。
代码:
class Solution {
public Node connect(Node root) {
if(root == null) return null;
//左节点
if(root.left != null){
//如果同节点右节点存在
if(root.right != null){
root.left.next = root.right;
}else{
//如果不存在,求出root下一个节点的最近子节点
root.left.next = getNextNode(root.next);
}
}
//右节点
if(root.right != null){
root.right.next = getNextNode(root.next);
}
//先递归右子树,只有当右子树连接完全后才能得到正确的左子树结果
connect(root.right);
connect(root.left);
return root;
}
private Node getNextNode(Node root){
if(root == null) return null;
//先返回左节点
if(root.left != null) return root.left;
if(root.right != null) return root.right;
return getNextNode(root.next);
}
}
124. 二叉树中的最大路径和
给定一个非空二叉树,返回其最大路径和。
本题中,路径被定义为一条从树中任意节点出发,达到任意节点的序列。该路径至少包含一个节点,且不一定经过根节点。
示例 1:
输入: [1,2,3]
1
/ \
2 3
输出: 6
示例 2:
输入: [-10,9,20,null,null,15,7]
-10
/ \
9 20
/ \
15 7
输出: 42
思路:
如果一个节点在最大路径和上,有两种情况:1.当前节点值和左右子树的最大值求和,然后回溯到父节点;2.当前节点值和左右子树的和为最大值。
代码:
class Solution {
private int sum = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
if(root == null) return 0;
helper(root);
return sum;
}
//如果一个节点在最大路径和上,分为两种情况
//1.当前节点值和左右子树的最大值求和,然后回溯到父节点
//2.当前节点值和左右子树的和为最大值
private int helper(TreeNode root){
if(root == null) return 0;
//如果和为负数,则直接返回0,表示忽略子树的负数值
int left = Math.max(0,helper(root.left));
int right = Math.max(0,helper(root.right));
sum = Math.max(left+right+root.val,sum); //求出最大值
return Math.max(left,right)+root.val;
}
}
129. 求根到叶子节点数字之和
给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。
例如,从根到叶子节点路径 1->2->3 代表数字 123。
计算从根到叶子节点生成的所有数字之和。
说明: 叶子节点是指没有子节点的节点。
示例 1:
输入: [1,2,3]
1
/ \
2 3
输出: 25
解释:
从根到叶子节点路径 1->2 代表数字 12.
从根到叶子节点路径 1->3 代表数字 13.
因此,数字总和 = 12 + 13 = 25.
示例 2:
输入: [4,9,0,5,1]
4
/ \
9 0
/ \
5 1
输出: 1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495.
从根到叶子节点路径 4->9->1 代表数字 491.
从根到叶子节点路径 4->0 代表数字 40.
因此,数字总和 = 495 + 491 + 40 = 1026.
思路:
当前节点代表的数字 = 上一节点代表的数字 * 10 + 当前节点值
递归求出左右子树的值,相加即可
代码:
class Solution {
public int sumNumbers(TreeNode root) {
if(root == null) return 0;
return getSum(root,0);
}
private int getSum(TreeNode root,int value){
if(root == null) return 0;
if(root.left == null && root.right == null){
return value * 10 + root.val;
}
int left = getSum(root.left,value * 10 + root.val);
int right = getSum(root.right,value * 10 + root.val);
return left + right;
}
}
173. 二叉搜索树迭代器
实现一个二叉搜索树迭代器。你将使用二叉搜索树的根节点初始化迭代器。
调用 next() 将返回二叉搜索树中的下一个最小的数。
示例:
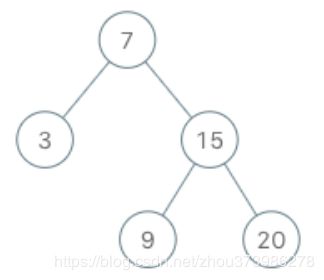
BSTIterator iterator = new BSTIterator(root); iterator.next(); // 返回 3 iterator.next(); // 返回 7 iterator.hasNext(); // 返回 true iterator.next(); // 返回 9 iterator.hasNext(); // 返回 true iterator.next(); // 返回 15 iterator.hasNext(); // 返回 true iterator.next(); // 返回 20 iterator.hasNext(); // 返回 false
思路:
BST的中序遍历结果即为其节点值的升序结果,所以直接对BST进行中序遍历,然后逐个返回值即可
代码:
class BSTIterator {
private List res = new ArrayList<>();
public BSTIterator(TreeNode root) {
Stack stack = new Stack<>();
TreeNode cur = root;
while(!stack.isEmpty() || cur != null){
if(cur != null){
stack.push(cur);
cur = cur.left;
}else{
cur = stack.pop();
res.add(cur.val);
cur = cur.right;
}
}
}
/** @return the next smallest number */
public int next() {
if(res.size() > 0){
return res.remove(0);
}
return 0;
}
/** @return whether we have a next smallest number */
public boolean hasNext() {
return res.size() != 0;
}
}
/**
* Your BSTIterator object will be instantiated and called as such:
* BSTIterator obj = new BSTIterator(root);
* int param_1 = obj.next();
* boolean param_2 = obj.hasNext();
*/
199. 二叉树的右视图
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例:
输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:
1 <---
/ \
2 3 <---
\ \
5 4 <---
思路:
1.层序遍历,保留每一层最后一个元素即可。
2.递归法:
本题的实质是每层取最右边的元素,所以在递归时,如果当前层数和目标集合中数相同,则表示还没有取最右元素,优先遍历右子树取出即可。
代码:
1.层序遍历
class Solution {
public List rightSideView(TreeNode root) {
List res = new ArrayList<>();
if(root == null) return res;
Queue queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
int count = queue.size();
while(count > 0){
count--;
TreeNode cur = queue.poll();
if(count == 0){
res.add(cur.val);
}
if(cur.left != null){
queue.add(cur.left);
}
if(cur.right != null){
queue.add(cur.right);
}
}
}
return res;
}
}
2.递归法:
class Solution {
public List rightSideView(TreeNode root) {
List res = new ArrayList<>();
getRightNode(root,res,0);
return res;
}
//每层取最右边的元素
private void getRightNode(TreeNode root,List res,int depth){
if(root == null) return;
if(depth == res.size()){
res.add(root.val);
}
//优先遍历右边
getRightNode(root.right,res,depth+1);
getRightNode(root.left,res,depth+1);
}
}
222. 完全二叉树的节点个数
给出一个完全二叉树,求出该树的节点个数。
说明:
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例:
输入:
1
/ \
2 3
/ \ /
4 5 6
输出: 6
思路:
使用递归法,迭代处理左子树和右子树,返回和相加再加1即可。
代码:
class Solution {
public int countNodes(TreeNode root) {
if(root == null) return 0;
return 1+ countNodes(root.left)+countNodes(root.right);
}
}
226. 翻转二叉树
翻转一棵二叉树。
示例:
输入:
4
/ \
2 7
/ \ / \
1 3 6 9
输出:
4
/ \
7 2
/ \ / \
9 6 3 1
思路:
递归法,创建一个TreeNode变量,用来交换左右节点,然后递归处理左右子树即可
代码:
class Solution {
public TreeNode invertTree(TreeNode root) {
if(root == null) return null;
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
invertTree(root.left);
invertTree(root.right);
return root;
}
}
230. 二叉搜索树中第K小的元素
给定一个二叉搜索树,编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。
说明:
你可以假设 k 总是有效的,1 ≤ k ≤ 二叉搜索树元素个数。
示例 1:
输入: root = [3,1,4,null,2], k = 1
3
/ \
1 4
\
2
输出: 1
示例 2:
输入: root = [5,3,6,2,4,null,null,1], k = 3
5
/ \
3 6
/ \
2 4
/
1
输出: 3
思路:
BST的中序遍历结果为其节点值的升序结果,这里优化了一下,在获取中序遍历的过程中比较k值,当遍历到第k大的节点时直接返回。递归法也是可以处理的,思路一样。
代码:
class Solution {
public int kthSmallest(TreeNode root, int k) {
//对于BST,中序遍历的结果就是BST从小到大的结果
if(k <= 0) return 0;
if(root == null) return 0;
Stack stack = new Stack<>();
TreeNode cur = root;
int count = 0;
while(!stack.isEmpty() || cur != null){
if(cur != null){
stack.push(cur);
cur = cur.left;
}else{
cur = stack.pop();
count++;
if(count == k){
return cur.val;
}
cur = cur.right;
}
}
return 0;
}
}
235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
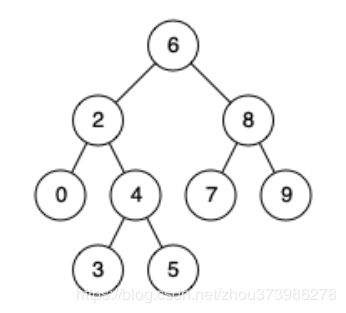
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。
思路:
根据BST的性质,最近公共祖先一定在[p,q]之间。如果当前root比两个值都大,说明最近公共祖先在左子树;如果当前root比两个值都小,说明最近公共祖先在右子树
代码:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//如果当前root比两个值都大,说明最近公共祖先在左子树
if(root.val > p.val && root.val > q.val){
return lowestCommonAncestor(root.left,p,q);
}else if(root.val < p.val && root.val < q.val){
//如果当前root比两个值都小,说明最近公共祖先在右子树
return lowestCommonAncestor(root.right,p,q);
}else{
//在中间
return root;
}
}
}
257. 二叉树的所有路径
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
输入:
1
/ \
2 3
\
5
输出: ["1->2->5", "1->3"]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
思路:
前序遍历,path添加当前节点值,递归左右子树时添加“->”,如果到达叶子节点,则将path加入集合
代码:
class Solution {
private List res = new ArrayList<>();
public List binaryTreePaths(TreeNode root) {
if(root == null) return res;
printRoute(root,"");
return res;
}
private void printRoute(TreeNode root,String path){
if(root == null) return ;
path += root.val;
if(root.left != null){
printRoute(root.left,path+"->");
}
if(root.right != null){
printRoute(root.right,path+"->");
}
if(root.left == null && root.right == null){
res.add(path);
}
}
}
297. 二叉树的序列化与反序列化
序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
示例:
你可以将以下二叉树:
1
/ \
2 3
/ \
4 5
序列化为 "[1,2,3,null,null,4,5]"
提示: 这与 LeetCode 目前使用的方式一致,详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式,你也可以采用其他的方法解决这个问题。
说明: 不要使用类的成员 / 全局 / 静态变量来存储状态,你的序列化和反序列化算法应该是无状态的。
思路:
对于普通二叉树,前序遍历和中序遍历、中序遍历和后序遍历可以确定唯一的二叉树。这题的实质就是在序列化方法中将树转变为可确定唯一二叉树的节点序列,反序列化就是根据节点序列构建二叉树。一开始我是通过构建前序和中序来解这道题,但是因为某个样例太大不能AC。所以考虑使用层序遍历来解这道题,因为序列化和反序列都只需要遍历节点一次,所以比较高效。
序列化过程即为层序遍历过程,而反序列化就是层序遍历的逆过程。
代码:
public class Codec {
public String serialize(TreeNode root) {
//层序遍历
if (root == null) return "";
StringBuilder sb = new StringBuilder();
Queue queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
int count = queue.size();
while (count > 0) {
count--;
TreeNode cur = queue.poll();
if (cur != null) {
sb.append(cur.val + ",");
queue.add(cur.left);//如果子节点为null也是可以加进去的
queue.add(cur.right);
} else {
sb.append("null,");
}
}
}
return sb.toString();
}
// Decodes your encoded data to tree.
//解析:1,2,3,null,null,4,5,null,null,null,null,
public TreeNode deserialize(String data) {
if (data.equals("")) return null;
//层序遍历还原
String[] nodes = data.split(",");
TreeNode root = new TreeNode(Integer.valueOf(nodes[0]));
Queue queue = new LinkedList<>();
queue.add(root);
int index = 1;
while(!queue.isEmpty()){
int count = queue.size();
while(count > 0){
count--;
TreeNode cur = queue.poll();
if(!nodes[index].equals("null")) {
cur.left = new TreeNode(Integer.valueOf(nodes[index++]));
}else{
cur.left = null;
index++;
}
if(!nodes[index].equals("null")){
cur.right = new TreeNode(Integer.valueOf(nodes[index++]));
}else{
cur.right = null;
index++;
}
if(cur.left != null){
queue.add(cur.left);
}
if(cur.right != null){
queue.add(cur.right);
}
}
}
return root;
}
}
// Your Codec object will be instantiated and called as such:
// Codec codec = new Codec();
// codec.deserialize(codec.serialize(root));
404. 左叶子之和
计算给定二叉树的所有左叶子之和。
示例:
3
/ \
9 20
/ \
15 7
在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
思路:
前序遍历,判断当前节点是否是左叶子节点,是的话就累加。
代码:
class Solution {
private int sum = 0;
public int sumOfLeftLeaves(TreeNode root) {
if(root == null) return 0;
//判断是否有左叶子
if(root.left != null){
if(root.left.left == null && root.left.right == null){
sum += root.left.val;
}
}
sumOfLeftLeaves(root.left);
sumOfLeftLeaves(root.right);
return sum;
}
}
429. N叉树的层序遍历
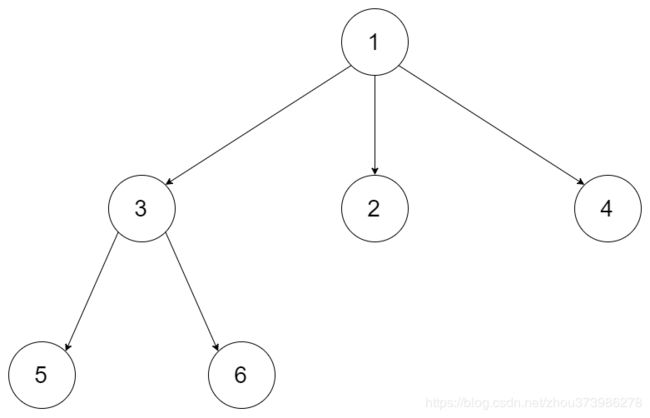
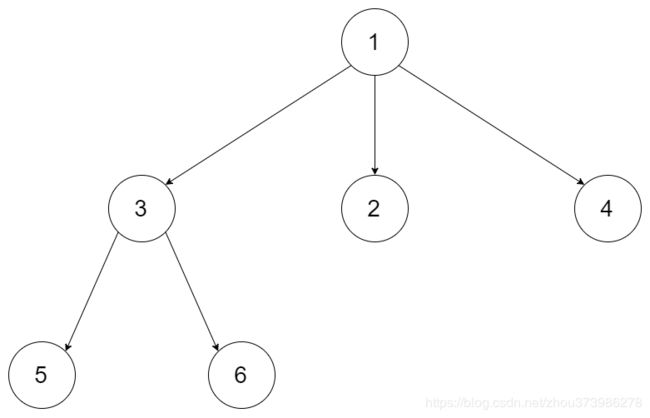
给定一个 N 叉树,返回其节点值的层序遍历。 (即从左到右,逐层遍历)。
[
[1],
[3,2,4],
[5,6]
]
思路:
层序遍历和二叉树的层序遍历类似,只是N叉树加入队列中的子节点不是左右儿子,而是孩子集合。
代码:
/*
// Definition for a Node.
class Node {
public int val;
public List children;
public Node() {}
public Node(int _val,List _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public List> levelOrder(Node root) {
List> res = new ArrayList<>();
if(root == null) return res;
Queue queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
int count = queue.size();
List list = new LinkedList<>();
while(count > 0){
count--;
Node cur = queue.poll();
list.add(cur.val);
for(Node node:cur.children){
queue.add(node);
}
}
res.add(list);
}
return res;
}
}
437. 路径总和 III
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。
示例:
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1
返回 3。和等于 8 的路径有:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11
思路:
1.判断一个根节点是否有满足条件的路径:
进行前序遍历,sum逐个减去节点值,如果为0则满足条件
2.然后使用前序遍历判断树中每个节点是否有满足条件的路径
代码:
class Solution {
private int pathNum = 0;
public int pathSum(TreeNode root, int sum) {
if(root == null) return 0;
//前序遍历每个节点,判断是否有路径和
isSum(root,sum);
pathSum(root.left,sum);
pathSum(root.right,sum);
return pathNum;
}
//判断当前节点是否有路径和为sum
private void isSum(TreeNode root,int sum){
if(root == null) return;
sum -= root.val;
if(sum == 0)
pathNum++;
isSum(root.left,sum);
isSum(root.right,sum);
}
}
449. 序列化和反序列化二叉搜索树
序列化是将数据结构或对象转换为一系列位的过程,以便它可以存储在文件或内存缓冲区中,或通过网络连接链路传输,以便稍后在同一个或另一个计算机环境中重建。
设计一个算法来序列化和反序列化二叉搜索树。 对序列化/反序列化算法的工作方式没有限制。 您只需确保二叉搜索树可以序列化为字符串,并且可以将该字符串反序列化为最初的二叉搜索树。
编码的字符串应尽可能紧凑。
注意:不要使用类成员/全局/静态变量来存储状态。 你的序列化和反序列化算法应该是无状态的。
思路:
如果是一个普通二叉树,需要前序和中序,或者后序和中序两个序列,才能唯一确定二叉树结构,而二叉搜索树,由于各元素之间有左子节点小于父节点再小于右子节点的性质,因此用一个前序排列就可以确定出唯一结构。
代码:
注意坑:[1,2]和[2,1]的情况
public class Codec {
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
//获得前序序列
if(root == null) return "";
String res = root.val + ",";
res += serialize(root.left);
res += serialize(root.right);
return res;
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
//根据前序序列构造TreeNode
if(data.equals("") || data == null) return null;
String[] valArr = data.split(",");
return build(valArr,0,valArr.length-1);
}
private TreeNode build(String[] arr,int lo,int hi){
if(lo > hi) return null;
if(lo == hi){
return new TreeNode(Integer.valueOf(arr[lo]));
}
TreeNode root = new TreeNode(Integer.valueOf(arr[lo]));
//找出左子节点和右子节点的分界点
int i;
for(i = lo + 1;i <= hi;i++){
if(Integer.valueOf(arr[i]) > Integer.valueOf(arr[lo])){
break;
}
}
root.left = build(arr,lo+1,i-1);
root.right = build(arr,i,hi);
return root;
}
}
450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
说明: 要求算法时间复杂度为 O(h),h 为树的高度。
示例:
root = [5,3,6,2,4,null,7]
key = 3
5
/ \
3 6
/ \ \
2 4 7
给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
5
/ \
4 6
/ \
2 7
另一个正确答案是 [5,2,6,null,4,null,7]。
5
/ \
2 6
\ \
4 7
思路:
采用递归法,每次递归返回当前子树的根节点。
根据BST的特点,首先比较当前节点和待删除值的大小,如果小于当前节点,则待删除的元素一定在左子树,则进一步递归处理左子节点;如果大于当前节点,则递归处理右子节点;如果等于当前节点,则删除当前节点,返回处理后的节点,一共有三种情况:
1.当被删除节点的左子结点为null,直接返回其右子节点;
2.当被删除节点的右子节点为N=null,直接返回左子节点;
(以上两种情况包括了左右子节点都不存在情况)
3.如果左右子节点都存在,则顶上去的节点为被删除节点右子树的最左边的子节点。找到顶上去的节点的,分别构造其左右子树。
代码:
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if(root == null) return null;
//如果Key<根节点,则递归查询其左子树
if(key < root.val){
root.left = deleteNode(root.left, key);
return root;
}else if(key > root.val){
root.right = deleteNode(root.right, key);
return root;
}else{
//key == root.val,找到待删除节点
//1.如果该节点的左节点为null,则返回右节点
if(root.left == null){
return root.right;
}else if(root.right == null){
//2.如果该节点的右节点为null,则返回左节点
return root.left;
}else{
//3.如果左右节点都不为null,则返回右子树的最左子节点
TreeNode newNode = getLeft(root.right);
//注意:这里一定要先构造右节点,然后再构造左节点,因为构造右节点会调用deleteLeft方法,这个方法会调用Node.left方法,如果提前构建了左子树,则会造成超时
newNode.right = deleteLeft(root.right);
newNode.left = root.left;
return newNode;
}
}
}
private TreeNode getLeft(TreeNode node){
if (node.left == null) {
return node;
}
return getLeft(node.left);
}
private TreeNode deleteLeft(TreeNode node){
if(node.left == null)
return node.right;
node.left = deleteLeft(node.left);
return node;
}
}
501. 二叉搜索树中的众数
给定一个有相同值的二叉搜索树(BST),找出 BST 中的所有众数(出现频率最高的元素)。
例如:
给定 BST [1,null,2,2],
1
\
2
/
2
返回[2].
提示:如果众数超过1个,不需考虑输出顺序
思路:
BST的中序遍历结果为节点的增序序列,所以根据这个序列可以求出众数。这里考虑在遍历途中判定众数。设定一个变量储存上一个节点的值,curTimes用来记录当前节点出现的次数,maxTimes用来记录目前出现的最大次数,如果上一个节点的值等于当前节点值,则curTimes+1,如果不等于则重新定义为1。然后判断如果curTimes等于maxTimes,则将当前节点值存入集合,如果大于maxTimes,则清空集合,并更新maxTimes,最后集合中存储的就是众数。
代码:
class Solution {
int preVal = 0,curTimes = 0,maxTimes = 0;
List res = new ArrayList<>();
public int[] findMode(TreeNode root) {
if(root == null) return new int[0];
inOrder(root);
int[] resArr = new int[res.size()];
for(int i = 0;i < res.size();i++){
resArr[i] = res.get(i);
}
return resArr;
}
private void inOrder(TreeNode root){
if(root == null) return;
//中序遍历
inOrder(root.left);
//判断当前值与上一个值的关系, 更新 curTimes 和 preVal
if(preVal == root.val){
curTimes++;
}else{
preVal = root.val;
curTimes = 1;
}
//判断当前数量与最大数量的关系, 更新 list 和 maxTimes
if(curTimes == maxTimes){
res.add(root.val);
}else if(curTimes > maxTimes){
res.clear();
res.add(root.val);
maxTimes = curTimes;
}
inOrder(root.right);
}
}
508. 出现次数最多的子树元素和
给出二叉树的根,找出出现次数最多的子树元素和。一个结点的子树元素和定义为以该结点为根的二叉树上所有结点的元素之和(包括结点本身)。然后求出出现次数最多的子树元素和。如果有多个元素出现的次数相同,返回所有出现次数最多的元素(不限顺序)。
示例 1
输入:
5
/ \
2 -3
返回 [2, -3, 4],所有的值均只出现一次,以任意顺序返回所有值。
示例 2
输入:
5
/ \
2 -5
返回 [2],只有 2 出现两次,-5 只出现 1 次。
思路:
该题的意思是求出二叉树所有子树(包括包含根节点的树)的元素和,然后求出出现元素和次数最多的那些。因为需要求子树,所以肯定是递归最为方便。定义一个map,在遍历时记录子树的元素和,同时求出出现的最大次数,然后对应map求出Key
代码:
class Solution {
private int max = 0;
public int[] findFrequentTreeSum(TreeNode root) {
if(root == null) return new int[0];
Map map = new HashMap<>();
helper(root,map);
//然后求出map中value最大值对应的Key
List res = new LinkedList<>();
for(Integer i : map.keySet()){
if(map.get(i) == max)
res.add(i);
}
int[] resArr = new int[res.size()];
for(int i = 0;i < res.size();i++){
resArr[i] = res.get(i);
}
return resArr;
}
private int helper(TreeNode root,Map map){
if(root == null) return 0;
//求出当前节点为根的元素和
int left = helper(root.left,map);
int right = helper(root.right,map);
int val = left+right+root.val;
map.put(val,map.getOrDefault(val,0)+1);
max = Math.max(max,map.get(val));
return val;
}
}
513. 找树左下角的值
给定一个二叉树,在树的最后一行找到最左边的值。
示例 1:
输入:
2
/ \
1 3
输出:
1
示例 2:
输入:
1
/ \
2 3
/ / \
4 5 6
/
7
输出:
7
思路:
层序遍历,遍历每层时都保存第一个元素,当遍历结束时即获得结果
代码:
class Solution {
public int findBottomLeftValue(TreeNode root) {
if(root == null) return 0;
//层序遍历,获取每层第一个元素,最终结果就是最后一层的第一个结果,遍历完成就得到
Queue queue = new LinkedList<>();
queue.add(root);
int res = 0;
while(!queue.isEmpty()){
int count = queue.size();
int size = queue.size();
while(count > 0){
TreeNode cur = queue.poll();
if(count == size){
res = cur.val;
}
count--;
if(cur.left != null){
queue.add(cur.left);
}
if(cur.right != null){
queue.add(cur.right);
}
}
}
return res;
}
}
515. 在每个树行中找最大值
您需要在二叉树的每一行中找到最大的值。
示例:
输入:
1
/ \
3 2
/ \ \
5 3 9
输出: [1, 3, 9]
思路:
方法1:使用迭代法层序遍历,每遍历一层的元素时都要求出最大值,放入结果集合中。
代码:
class Solution {
public List largestValues(TreeNode root) {
List res = new ArrayList<>();
if(root == null) return res;
Queue queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
int count = queue.size();
int max = Integer.MIN_VALUE;
while(count > 0){
count--;
TreeNode cur = queue.poll();
max = Math.max(max,cur.val);
if(cur.left != null){
queue.add(cur.left);
}
if(cur.right != null){
queue.add(cur.right);
}
}
res.add(max);
}
return res;
}
}
思路:
方法2:递归。深度优先搜索,遍历时传入List和当前节点对应的高度,高度h的最大值是list.get(h),每遍历到一个节点就根据所在的高度和保存的最大值比较即可。
对于这种求每层xxx的题目,可以使用List储存每层的结果,而层数对应List的索引(从0开始)
代码:
public List largestValues1(TreeNode root) {
List res = new ArrayList<>();
helper(root, res, 0);
return res;
}
private void helper(TreeNode root, List res, int depth) {
if (root == null) return;
//首次访问depth层的元素
if (depth + 1 > res.size()) {
res.add(root.val);
}
//比较当前节点和当前层最大值
if(root.val > res.get(depth)){
res.set(depth,root.val);
}
//递归
helper(root.left,res,depth+1);
helper(root.right,res,depth+1);
}
530. 二叉搜索树的最小绝对差
给定一个所有节点为非负值的二叉搜索树,求树中任意两节点的差的绝对值的最小值。
示例 :
输入:
1
\
3
/
2
输出:
1
解释:
最小绝对差为1,其中 2 和 1 的差的绝对值为 1(或者 2 和 3)。
注意: 树中至少有2个节点。
思路:
BST的中序遍历得到的是节点值的升序序列,所以求差的最小值一定是在升序序列相邻元素之间。为了优化空间,在递归求升序序列时就求出最小差值
代码:
class Solution {
private List res = new ArrayList<>();
private int min = 0;
public int getMinimumDifference(TreeNode root) {
if(root == null) return 0;
getInorder(root);
return min;
}
private void getInorder(TreeNode node){
if(node == null) return;
getInorder(node.left);
res.add(node.val);
int size = res.size();
if(size == 2){
min = res.get(1) - res.get(0);
}else if(size>2){
min = Math.min((res.get(size-1)-res.get(size-2)),min);
}
getInorder(node.right);
}
}
538. 把二叉搜索树转换为累加树
给定一个二叉搜索树(Binary Search Tree),把它转换成为累加树(Greater Tree),使得每个节点的值是原来的节点值加上所有大于它的节点值之和。
例如:
输出: 转换为累加树:

思路:
将BST的节点通过右→中→左顺序遍历,得到的结果是BST从大到小的节点值,如上述BST为[6,5,4,3,2,1],因此在遍历途中,当前节点添加上个累加节点值即可
代码:
class Solution {
private int pre = 0;
public TreeNode convertBST(TreeNode root) {
if(root == null) return null;
getInorder(root);
return root;
}
//从右到左获取节点值
private void getInorder(TreeNode root){
if(root == null) return;
getInorder(root.right);
//当前节点更新
root.val += pre;
pre = root.val;
getInorder(root.left);
}
}
543. 二叉树的直径
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过根结点。
示例 :
给定二叉树
1
/ \
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
思路:
同124题。
如果一个节点在最长路径上,分为两种情况:
1.该节点和左右子树中的最长路径,回溯到父节点
2.该节点和左右子树组成最长路径
代码:
class Solution {
private int sum = 0;
public int diameterOfBinaryTree(TreeNode root) {
if(root == null) return 0;
getMax(root);
return sum;
}
private int getMax(TreeNode root){
if(root == null) return 0;
int left = getMax(root.left);
int right = getMax(root.right);
sum = Math.max(sum,left+right);
return Math.max(left,right)+1;
}
}
559. N叉树的最大深度
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
思路:
最大深度在根节点的某个子节点上,使用递归和层序遍历均可,参照二叉树的最大深度。
代码:
class Solution {
public int maxDepth(Node root) {
if(root == null) return 0;
int max = 0;
//求出根节点每个子节点的最大深度
for(Node node : root.children){
max = Math.max(max,maxDepth(node));
}
return max+1;
}
}
563. 二叉树的坡度
给定一个二叉树,计算整个树的坡度。
一个树的节点的坡度定义即为,该节点左子树的结点之和和右子树结点之和的差的绝对值。空结点的的坡度是0。
整个树的坡度就是其所有节点的坡度之和。
示例:
输入:
1
/ \
2 3
输出: 1
解释:
结点的坡度 2 : 0
结点的坡度 3 : 0
结点的坡度 1 : |2-3| = 1
树的坡度 : 0 + 0 + 1 = 1
思路:
采用后续遍历,从底层元素开始,计算对应节点的坡度并累加,遍历返回每个子节点的子树节点和。
代码:
class Solution {
int res = 0;
public int findTilt(TreeNode root) {
helper(root);
return res;
}
//后序遍历,从底层开始计算坡度差,返回每个子树节点的节点和;
private int helper(TreeNode root){
if(root == null) return 0;
int left = helper(root.left);
int right = helper(root.right);
res += Math.abs(left - right);
return left+right+root.val;
}
}
572. 另一个树的子树
给定两个非空二叉树 s 和 t,检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。
示例 1:
给定的树 s:
3
/ \
4 5
/ \
1 2
给定的树 t:
4
/ \
1 2
返回 true,因为 t 与 s 的一个子树拥有相同的结构和节点值。
示例 2:
给定的树 s:
3
/ \
4 5
/ \
1 2
/
0
给定的树 t:
4
/ \
1 2
返回 false。
思路:
两个前序遍历:
1.比较节点是否和t相同:前序遍历,如果根节点值不同,则返回false,否则递归比较左右子树。
2.比较s上每个节点是否和t相同:前序遍历,如果有一个节点满足条件,直接返回true
代码:
class Solution {
public boolean isSubtree(TreeNode s, TreeNode t) {
if(t == null) return true;
if(s == null) return false;
//比较当前节点是否与t相同
return helper(s,t) || isSubtree(s.left,t) ||isSubtree(s.right,t);
}
private boolean helper(TreeNode s,TreeNode t){
if(s == null && t == null)
return true;
if(s == null || t == null)
return false;
if(s.val != t.val)
return false;
return helper(s.left,t.left) && helper(s.right,t.right);
}
}
606. 根据二叉树创建字符串
你需要采用前序遍历的方式,将一个二叉树转换成一个由括号和整数组成的字符串。
空节点则用一对空括号 “()” 表示。而且你需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
示例 1:
输入: 二叉树: [1,2,3,4]
1
/ \
2 3
/
4
输出: "1(2(4))(3)"
解释: 原本将是“1(2(4)())(3())”,
在你省略所有不必要的空括号对之后,
它将是“1(2(4))(3)”。
示例 2:
输入: 二叉树: [1,2,3,null,4]
1
/ \
2 3
\
4
输出: "1(2()(4))(3)"
解释: 和第一个示例相似,
除了我们不能省略第一个对括号来中断输入和输出之间的一对一映射关系。
思路:
创建StringBuilder添加字符串,进行前序遍历。在添加时判断是否需要添加"()",有两种情况"()“可以省略:
1.左子树存在而右子树为空;
2.左右子树都为空。
所以左子树为空右子树存在时需要添加”()"。
代码:
class Solution {
StringBuilder sb = new StringBuilder();
public String tree2str(TreeNode t) {
if(t == null) return "";
helper(t);
return sb.substring(1,sb.length()-1).toString();
}
private void helper(TreeNode root){
if(root == null) return ;
sb.append("(");
sb.append(root.val);
//如果左子节点为null且右节点不为Null,不能省略空括号
if(root.left == null && root.right != null){
sb.append("()");
}else{
helper(root.left);
}
helper(root.right);
sb.append(")");
}
}
617. 合并二叉树
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:
输入:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
输出:
合并后的树:
3
/ \
4 5
/ \ \
5 4 7
注意: 合并必须从两个树的根节点开始。
思路:
在t1的基础上合并树,如果一个节点为null,返回另一个节点,这种情况包括:t1/t2均为null,t1为null/t2不为null,t2为null/t1不为null。然后合并两个根节点值,在递归合并左右子树。
代码:
class Solution {
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
/*if(t1 == null && t2 == null) return null;
if(t1 == null && t2 != null){
return t2;
}else if(t1 != null && t2 == null){
return t1;
}*/
if(t1 == null) return t2;
if(t2 == null) return t1;
//合并根节点
t1.val += t2.val;
//递归合并左右子树
t1.left = mergeTrees(t1.left,t2.left);
t1.right = mergeTrees(t1.right,t2.right);
return t1;
}
}
623. 在二叉树中增加一行
给定一个二叉树,根节点为第1层,深度为 1。在其第 d 层追加一行值为 v 的节点。
添加规则:给定一个深度值 d (正整数),针对深度为 d-1 层的每一非空节点 N,为 N 创建两个值为 v 的左子树和右子树。
将 N 原先的左子树,连接为新节点 v 的左子树;将 N 原先的右子树,连接为新节点 v 的右子树。
如果 d 的值为 1,深度 d - 1 不存在,则创建一个新的根节点 v,原先的整棵树将作为 v 的左子树。
示例 1:
输入:
二叉树如下所示:
4
/ \
2 6
/ \ /
3 1 5
v = 1
d = 2
输出:
4
/ \
1 1
/ \
2 6
/ \ /
3 1 5
示例 2:
输入:
二叉树如下所示:
4
/
2
/ \
3 1
v = 1
d = 3
输出:
4
/
2
/ \
1 1
/ \
3 1
思路:
层序遍历,按照题目要求写代码即可
代码:
class Solution {
public TreeNode addOneRow(TreeNode root, int v, int d) {
if(d <= 0) return null;
if(d == 1) {
TreeNode newRoot = new TreeNode(v);
newRoot.left = root;
return newRoot;
}
//层序遍历
Queue queue = new LinkedList<>();
queue.add(root);
int depth = 0;
while(!queue.isEmpty()){
int count = queue.size();
depth++;
while(count > 0){
count--;
TreeNode cur = queue.poll();
//添加下一层节点
if(cur.left != null){
queue.add(cur.left);
}
if(cur.right != null){
queue.add(cur.right);
}
if(d - 1 == depth){
//给d-1层节点添加新节点
createNode(cur,v);
}
}
}
return root;
}
private void createNode(TreeNode cur,int v){
TreeNode left = cur.left;
TreeNode right = cur.right;
TreeNode newLeft = new TreeNode(v);
TreeNode newRight = new TreeNode(v);
newLeft.left = left;
newRight.right = right;
cur.left = newLeft;
cur.right = newRight;
}
}
637. 二叉树的层平均值
给定一个非空二叉树, 返回一个由每层节点平均值组成的数组.
示例 1:
输入:
3
/ \
9 20
/ \
15 7
输出: [3, 14.5, 11]
解释:
第0层的平均值是 3, 第1层是 14.5, 第2层是 11. 因此返回 [3, 14.5, 11].
思路:
层序遍历的变形题
代码:
class Solution {
public List averageOfLevels(TreeNode root) {
List res = new ArrayList<>();
if(root == null) return res;
//层序遍历
Queue queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
int count = queue.size();
int size = count;
double sum = 0;
while(count > 0){
count--;
TreeNode cur = queue.poll();
sum += cur.val;
if(cur.left != null)
queue.add(cur.left);
if(cur.right != null)
queue.add(cur.right);
}
res.add(sum / size);
}
return res;
}
}
652. 寻找重复的子树
给定一棵二叉树,返回所有重复的子树。对于同一类的重复子树,你只需要返回其中任意一棵的根结点即可。
两棵树重复是指它们具有相同的结构以及相同的结点值。
示例 1:
1
/ \
2 3
/ / \
4 2 4
/
4
下面是两个重复的子树:
2
/
4
和
4
因此,你需要以列表的形式返回上述重复子树的根结点。
思路:
该题是为了比较是否有完全相同的子树,所以可以遍历获取当前节点的子树节点集合,并存入map中,如果在map中出现过1次,则为重复子树,节点加入结果集中。
代码:
class Solution {
public List findDuplicateSubtrees(TreeNode root) {
List res = new ArrayList<>();
HashMap map = new HashMap<>();
if(root == null) return res;
saveRoute(root,res,map);
return res;
}
//递归获取每个子树的路径,保存于Map中
private String saveRoute(TreeNode node,List res,HashMap map){
if(node == null) return "";
String route = node.val + "," + saveRoute(node.left,res,map) + "," + saveRoute(node.right,res,map);
//将结果放入map,判断是否有相同子树
//避免出现多次相同子树
if(map.get(route) != null && map.get(route) == 1){
res.add(node);
}
map.put(route,map.getOrDefault(route,0)+1);
return route;
}
}
653. 两数之和 IV - 输入 BST
给定一个二叉搜索树和一个目标结果,如果 BST 中存在两个元素且它们的和等于给定的目标结果,则返回 true。
案例 1:
输入:
5
/ \
3 6
/ \ \
2 4 7
Target = 9
输出: True
案例 2:
输入:
5
/ \
3 6
/ \ \
2 4 7
Target = 28
输出: False
思路:
BST中序遍历得到节点的升序结果,然后再采用双指针法,一个指针指向最右边,一个指向最左边,然后进行遍历比较,如果差值大于最左边的值,则将右边指针左移(即小值增大),如果小于最左边的值,则将左边指针右移(即大值减小),如果相等,则return true。注意这里的坑:在[1]中找2,必须要找到两个数,所以循环终止的判定条件需要注意。
当然这里还可以中序遍历将结果存入HashMap,然后遍历Map,判定是否有差值,坑也是同样的,需要判定差值出现的次数是否大于1
代码:
class Solution {
List list = new ArrayList<>();
public boolean findTarget(TreeNode root, int k) {
if(root == null) return false;
inorder(root);
//因为序列是升序,采用双指针法查找
int start = 0;
int end = list.size() - 1;
//注意:start不能等于end,因为不满足两个数的条件
while(start < end){
if(k - list.get(start) > list.get(end)){
//如果差值大于最大值,左边指针右移
start++;
}else if(k - list.get(start) < list.get(end)){
//如果差值小于最小值,右边指针左移
end--;
}else{
return true;
}
}
return false;
}
private void inorder(TreeNode root){
if(root == null) return;
//中序
inorder(root.left);
list.add(root.val);
inorder(root.right);
}
}
654. 最大二叉树
给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下:
二叉树的根是数组中的最大元素。
左子树是通过数组中最大值左边部分构造出的最大二叉树。
右子树是通过数组中最大值右边部分构造出的最大二叉树。
通过给定的数组构建最大二叉树,并且输出这个树的根节点。
Example 1:
输入: [3,2,1,6,0,5]
输入: 返回下面这棵树的根节点:
6
/ \
3 5
\ /
2 0
\
1
思路:
和之前构建树的思路类似,只要找出递归的范围即可。
代码:
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
if(nums.length == 0) return null;
return helper(nums,0,nums.length-1);
}
private TreeNode helper(int[] nums,int lo,int hi){
if(lo > hi) return null;
if(hi == lo) return new TreeNode(nums[lo]);
//找到最大值
int maxIndex = hi + 1;
int max = Integer.MIN_VALUE;
for(int i = lo;i <= hi;i++){
if(max < nums[i]){
maxIndex = i;
max = nums[i];
}
}
TreeNode root = new TreeNode(max);
//递归构建左右子树
root.left = helper(nums,lo,maxIndex-1);
root.right = helper(nums,maxIndex+1,hi);
return root;
}
}
655. 输出二叉树
在一个 m*n 的二维字符串数组中输出二叉树,并遵守以下规则:
行数 m 应当等于给定二叉树的高度。 列数 n 应当总是奇数。
根节点的值(以字符串格式给出)应当放在可放置的第一行正中间。根节点所在的行与列会将剩余空间划分为两部分(左下部分和右下部分)。你应该将左子树输出在左下部分,右子树输出在右下部分。左下和右下部分应当有相同的大小。即使一个子树为空而另一个非空,你不需要为空的子树输出任何东西,但仍需要为另一个子树留出足够的空间。然而,如果两个子树都为空则不需要为它们留出任何空间。
每个未使用的空间应包含一个空的字符串""。 使用相同的规则输出子树。
示例 1:
输入:
1
/
2
输出:
[["", "1", ""],
["2", "", ""]]
示例 2:
输入:
1
/ \
2 3
\
4
输出:
[["", "", "", "1", "", "", ""],
["", "2", "", "", "", "3", ""],
["", "", "4", "", "", "", ""]]
示例 3:
输入:
1
/ \
2 5
/
3
/
4
输出:
[["", "", "", "", "", "", "", "1", "", "", "", "", "", "", ""]
["", "", "", "2", "", "", "", "", "", "", "", "5", "", "", ""]
["", "3", "", "", "", "", "", "", "", "", "", "", "", "", ""]
["4", "", "", "", "", "", "", "", "", "", "", "", "", "", ""]]
思路:
1.求出树的最大深度,得到m,n = 2 ^ m -1,构建二维数组,初始化
2.填充二维数组,在中间位置插入根元素,递归插入左右子树
代码:
class Solution {
int n = 0,m = 0;
List> res = new ArrayList<>();
public List> printTree(TreeNode root) {
if(root == null) return null;
m = getMaxDepth(root);
n = (int)Math.pow(2,m) - 1;
for(int i = 0;i < m;i++){
List list = new ArrayList();
for(int j = 0;j < n;j ++)
list.add("");
res.add(list);
}
helper(root,0,n-1,0);
return res;
}
//构建集合
private void helper(TreeNode node,int lo,int hi,int depth){
if(node == null ||(lo > hi)) return;
//放入根节点
int mid = lo + (hi-lo) / 2;
res.get(depth).set(mid,node.val+"");
helper(node.left,lo,mid-1,depth+1);
helper(node.right,mid+1,hi,depth+1);
}
//求出最大深度
private int getMaxDepth(TreeNode root){
if(root == null) return 0;
return Math.max(getMaxDepth(root.left),getMaxDepth(root.right))+1;
}
}
662. 二叉树最大宽度
669. 修剪二叉搜索树
给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。
示例 1:
输入:
1
/ \
0 2
L = 1
R = 2
输出:
1
\
2
示例 2:
输入:
3
/ \
0 4
\
2
/
1
L = 1
R = 3
输出:
3
/
2
/
1
思路:
根据BST特性,如果根节点小于L,则舍弃左子树,递归处理右子树,如果根节点大于R,则舍弃右子树,递归处理左子树。然后对于不需要舍弃的节点,分别递归处理其左右节点即可。
代码:
class Solution {
public TreeNode trimBST(TreeNode root, int L, int R) {
if(root == null) return null;
if(R < L) return null;
//如果小于范围内,则在右边子树找寻
if(root.val < L){
return trimBST(root.right,L,R);
}
//如果大于范围内,则在左子树找寻
if(root.val > R){
return trimBST(root.left,L,R);
}
//接下来是满足条件不用删除
root.left = trimBST(root.left,L,R);
root.right = trimBST(root.right,L,R);
return root;
}
}
671. 二叉树中第二小的节点
给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话,那么这个节点的值不大于它的子节点的值。
给出这样的一个二叉树,你需要输出所有节点中的第二小的值。如果第二小的值不存在的话,输出 -1 。
示例 1:
输入:
2
/ \
2 5
/ \
5 7
输出: 5
说明: 最小的值是 2 ,第二小的值是 5 。
示例 2:
输入:
2
/ \
2 2
输出: -1
说明: 最小的值是 2, 但是不存在第二小的值。
思路:
本题的关键是根节点的值小于等于子节点,所以最小值一定出现的根节点。设定两个变量分别储存最小值和第二小的值,先求出最小值,最小值不为-1后求取第二小的值,如果当前节点大于最小值且第二小的值还没有给定,则获取当前节点值。如果第二小的值已经给定了,比较当前节点值和第二小的值哪个小,并将较小值赋值。
代码:
class Solution {
int min = -1,secondMin = -1;
public int findSecondMinimumValue(TreeNode root) {
if(root == null) return -1;
if(min == -1){
//最小值
min = root.val;
}else if(min < root.val){
if(secondMin == -1){
secondMin = root.val;
}else{
secondMin = Math.min(secondMin,root.val);
}
}
findSecondMinimumValue(root.left);
findSecondMinimumValue(root.right);
return secondMin;
}
}
687. 最长同值路径
给定一个二叉树,找到最长的路径,这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。
注意:两个节点之间的路径长度由它们之间的边数表示。
示例 1:
输入:
5
/ \
4 5
/ \ \
1 1 5
输出:
2
示例 2:
输入:
1
/ \
4 5
/ \ \
4 4 5
输出:
2
思路:
等同于124题
代码:
class Solution {
private int sum = 0;
public int longestUnivaluePath(TreeNode root) {
if(root == null) return 0;
helper(root,root.val);
return sum;
}
//1.左右节点返回较长通知路径,回溯父节点
//2.左右两边+根节点
private int helper(TreeNode root,int val){
if(root == null) return 0;
int left = helper(root.left,root.val);
int right = helper(root.right,root.val);
sum = Math.max(sum,left+right);
if(root.val == val)
return Math.max(left,right)+1;
return 0;
}
}
700. 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 NULL。
例如,
给定二叉搜索树:
4
/ \
2 7
/ \
1 3
和值: 2
你应该返回如下子树:
2
/ \
1 3
在上述示例中,如果要找的值是 5,但因为没有节点值为 5,我们应该返回 NULL。
思路:
递归法,如果当前节点的值为给出的值,则直接返回当前节点,根据BST的性质,如果给出值>当前节点值,则在当前节点的右子树递归查找,否则在当前节点的左子树递归查找。类似于数组的二分查找
代码:
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if(root == null) return null;
if(root.val == val){
return root;
}else if(root.val < val){
return searchBST(root.right,val);
}else{
return searchBST(root.left,val);
}
}
}
701. 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点和要插入树中的值,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 保证原始二叉搜索树中不存在新值。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。
例如,
给定二叉搜索树:
4
/ \
2 7
/ \
1 3
和 插入的值: 5
你可以返回这个二叉搜索树:
4
/ \
2 7
/ \ /
1 3 5
或者这个树也是有效的:
5
/ \
2 7
/ \
1 3
\
4
思路:
通过BST的性质,和插入值进行比较,如果插入值小于当前节点,则新节点在左子树,反之在右子树,递归,一直到叶子节点的子节点,添加新节点。
此题也可以用迭代法,思路和递归是一样的,即设定两个指针,一直遍历找到目标叶子节点,新增节点即可。
代码:
1.递归法
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if(root == null)
return new TreeNode(val);
if(val < root.val){
root.left = insertIntoBST(root.left,val);
}
if(val > root.val){
root.right = insertIntoBST(root.right,val);
}
return root;
}
}
2.迭代法:
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if(root == null) return null;
//迭代找出需要插入节点的叶子节点
TreeNode parent = root,p = root;
//使用两个指针,根据BST的特点找出需要插入的节点
while(p != null){
parent = p;
p = val > p.val ? p.right:p.left;
}
//插入新节点的parent节点后
if(parent.val > val){
parent.left = new TreeNode(val);
}else if(parent.val < val){
parent.right = new TreeNode(val);
}
return root;
}
}
783. 二叉搜索树结点最小距离
给定一个二叉搜索树的根结点 root, 返回树中任意两节点的差的最小值。
示例:
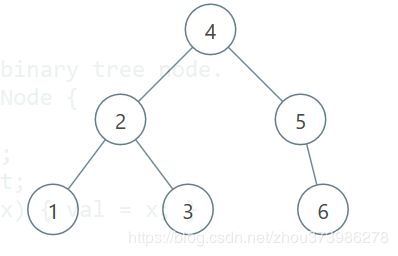
输入: root = [4,2,6,1,3,null,null]
输出: 1
解释:
注意,root是树结点对象(TreeNode object),而不是数组。
给定的树 [4,2,6,1,3,null,null] 可表示为下图:
4
/ \
2 6
/ \
1 3
最小的差值是 1, 它是节点1和节点2的差值, 也是节点3和节点2的差值。
思路:
返回BST的中序遍历结果,最小值一定在结果相邻两个元素之间,这里我做了一下优化,在递归中序遍历的过程中就进行了最小值计算,避免了中序遍历后再一次遍历得到的结果。
代码:
class Solution {
private List res = new ArrayList<>();
private int min = 0;
public int minDiffInBST(TreeNode root) {
//中序遍历,得到增序结果,第二个元素减去第一个即可
if(root == null) return 0;
getInorder(root);
return min;
}
private void getInorder(TreeNode node){
if(node == null) return;
getInorder(node.left);
res.add(node.val);
int size = res.size();
//因为得到的是中序结果,所以逐个求出相邻节点值之间差值的最小值即为结果
if(size == 2){
min = res.get(1) - res.get(0);
}else if(size > 2){
min = Math.min((res.get(size-1)-res.get(size-2)),min);
}
getInorder(node.right);
}
}
814. 二叉树剪枝
给定二叉树根结点 root ,此外树的每个结点的值要么是 0,要么是 1。返回移除了所有不包含 1 的子树的原二叉树。( 节点 X 的子树为 X 本身,以及所有 X 的后代。)
示例1:
输入: [1,null,0,0,1]
输出: [1,null,0,null,1]
解释:
只有红色节点满足条件“所有不包含 1 的子树”。
右图为返回的答案。
示例2:
输入: [1,0,1,0,0,0,1]
输出: [1,null,1,null,1]

示例3:
输入: [1,1,0,1,1,0,1,0]
输出: [1,1,0,1,1,null,1]

思路:
使用后续遍历,从最底层节点开始减去节点,如果节点是叶子节点且节点值为0,则减去,这样才不会漏掉。
代码:
class Solution {
public TreeNode pruneTree(TreeNode root) {
//后序遍历删除
if(root == null) return null;
root.left = pruneTree(root.left);
root.right = pruneTree(root.right);
if(root.left == null && root.right == null && root != null && root.val == 0){
root = null;
}
return root;
}
}
872. 叶子相似的树
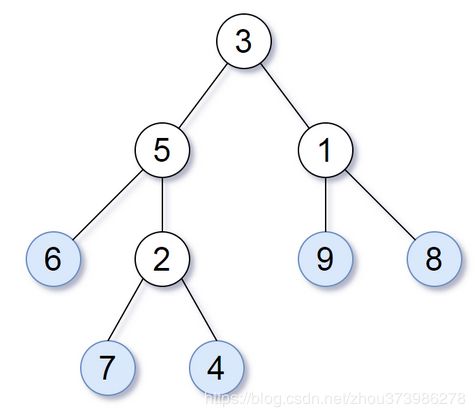
请考虑一颗二叉树上所有的叶子,这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。
举个例子,如上图所示,给定一颗叶值序列为 (6, 7, 4, 9, 8) 的树。
如果有两颗二叉树的叶值序列是相同,那么我们就认为它们是 叶相似 的。
如果给定的两个头结点分别为 root1 和 root2 的树是叶相似的,则返回 true;否则返回 false 。
思路:
首先构建递归方法,得到指定树的叶值序列,即在叶子节点时将节点值加入集合,递归处理左右节点即可。然后得到参数中两棵树的叶值序列,比较它们的顺序和大小即可。
代码:
class Solution {
public boolean leafSimilar(TreeNode root1, TreeNode root2) {
if(root1 == null || root2 == null ) return false;
List res1 = getLeafSort(root1);
List res2 = getLeafSort(root2);
if(res1.size() != res2.size()) return false;
for(int i = 0;i < res1.size();i++){
if(res1.get(i) != res2.get(i))
return false;
}
return true;
}
private List getLeafSort(TreeNode root){
List res = new ArrayList<>();
helper(root,res);
return res;
}
private void helper(TreeNode root,List res){
if(root == null) return;
if(root.left == null && root.right == null){
res.add(root.val);
}
helper(root.left,res);
helper(root.right,res);
}
}
889. 根据前序和后序遍历构造二叉树
返回与给定的前序和后序遍历匹配的任何二叉树。
pre 和 post 遍历中的值是不同的正整数。
示例:
输入:pre = [1,2,4,5,3,6,7], post = [4,5,2,6,7,3,1]
输出:[1,2,3,4,5,6,7]
思路:
和之前构造二叉树的思路是一致的。前序遍历数组的第一个元素为根节点,第二个节点为左子树的根节点,找到左子树根节点在后序遍历中的索引,前后分别为左右子树,可以求出左右子树的元素个数,进行递归
代码:
class Solution {
public TreeNode constructFromPrePost(int[] pre, int[] post) {
return build(pre,0,pre.length-1,post,0,post.length-1);
}
private TreeNode build(int[] pre,int preLo,int preHi,int[] post,int postLo,int postHi){
if(preLo > preHi || postLo > postHi) return null;
//前序遍历第一个节点为根节点
TreeNode root = new TreeNode(pre[preLo]);
if(preLo == preHi) return root;
int mid = -1;
if(preLo + 1 <= preHi){
for(int i = postLo;i <= postHi;i++){
//前序遍历第二个节点为左子树的根节点
if(post[i] == pre[preLo+1]){
mid = i;
break;
}
}
}
//左子树的节点数为:mid-postLo+1
root.left = build(pre,preLo+1,preLo+1+mid-postLo,post,postLo,mid);
//后续遍历的最后一个节点为根节点,所以递归时需要-1
root.right = build(pre,preLo+1+mid-postLo+1,preHi,post,mid+1,postHi-1);
return root;
}
}
897. 递增顺序查找树
给定一个树,按中序遍历重新排列树,使树中最左边的结点现在是树的根,并且每个结点没有左子结点,只有一个右子结点。
示例 :
输入:[5,3,6,2,4,null,8,1,null,null,null,7,9]
5
/ \
3 6
/ \ \
2 4 8
/ / \
1 7 9
输出:[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
1
\
2
\
3
\
4
\
5
\
6
\
7
\
8
\
9
思路:
中序遍历得到TreeNode的集合,然后遍历此集合,在节点的原有内存上修改子节点。
代码:
class Solution {
private List list = new ArrayList<>();
public TreeNode increasingBST(TreeNode root) {
if(root == null) return null;
TreeNode res = new TreeNode(0);
TreeNode res1 = res;
inorder(root);
for(TreeNode node : list){
res1.left = null;
res1.right = node;
res1 = res1.right;
}
res1.left = null;
res1.right = null;
return res.right;
}
public void inorder(TreeNode node){
if(node == null) return;
inorder(node.left);
list.add(node);
inorder(node.right);
}
}
938. 二叉搜索树的范围和
给定二叉搜索树的根结点 root,返回 L 和 R(含)之间的所有结点的值的和。
二叉搜索树保证具有唯一的值。
示例 1:
输入:root = [10,5,15,3,7,null,18], L = 7, R = 15
输出:32
示例 2:
输入:root = [10,5,15,3,7,13,18,1,null,6], L = 6, R = 10
输出:23
思路:
BST的中序遍历结果为其节点值的升序结果,用迭代和递归均可求出结果
代码:
1.层序遍历
class Solution {
private int sum = 0;
public int rangeSumBST(TreeNode root, int L, int R) {
if(L > R) return 0;
if(root == null) return 0;
Stack stack = new Stack<>();
TreeNode cur = root;
while(!stack.isEmpty() || cur != null){
if(cur != null){
stack.push(cur);
cur = cur.left;
}else{
cur = stack.pop();
if(cur.val >= L && cur.val <= R){
sum += cur.val;
}
cur = cur.right;
}
}
return sum;
}
}
2.递归法
class Solution {
private int sum = 0;
public int rangeSumBST(TreeNode root, int L, int R) {
if(root == null) return 0;
if(root.val >= L && root.val <= R){
sum += root.val;
}
rangeSumBST(root.left,L,R);
rangeSumBST(root.right,L,R);
return sum;
}
}
958. 二叉树的完全性检验
给定一个二叉树,确定它是否是一个完全二叉树。
百度百科中对完全二叉树的定义如下:
若设二叉树的深度为 h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。(注:第 h 层可能包含 1~ 2h 个节点。)
示例 1:
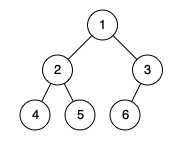
输入:[1,2,3,4,5,6]
输出:true
解释:最后一层前的每一层都是满的(即,结点值为 {1} 和 {2,3} 的两层),且最后一层中的所有结点({4,5,6})都尽可能地向左。
示例 2:
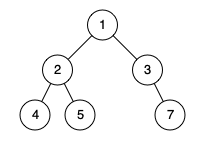
输入:[1,2,3,4,5,null,7]
输出:false
解释:值为 7 的结点没有尽可能靠向左侧。
思路:
层序遍历当前树,建立一个标记flag,如果遇到了null节点,则标记变为true,如果后续又遇到了非空节点,则标记变为false,因为只有最后节点为null才满足题目的情况,在其他地方出现非空节点不满足要求。
代码:
class Solution {
public boolean isCompleteTree(TreeNode root) {
if(root == null) return true;
boolean flag = false;
//层序遍历
Queue queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
int count = queue.size();
while(count > 0){
count--;
TreeNode cur = queue.poll();
//如果出现空节点,则标志变为true,如果在后面又出现非空节点,则标志变为false
if(cur == null){
flag = true;
continue;
}
if(flag) return false;
queue.add(cur.left);
queue.add(cur.right);
}
}
return flag;
}
}
965. 单值二叉树
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时,才返回 true;否则返回 false。
思路:
设定两个变量,用来储存当前节点的值和上个节点的值,如果上个节点有值且和当前节点不相等,则说明不满足要求,返回false,否则递归处理左右子树。
代码:
class Solution {
int pre = -1,cur = -1;
public boolean isUnivalTree(TreeNode root) {
if(root == null) return true;
pre = cur;
cur = root.val;
if(pre != -1 && cur != pre) return false;
return isUnivalTree(root.left) && isUnivalTree(root.right);
}
}
988. 从叶结点开始的最小字符串
给定一颗根结点为 root 的二叉树,书中的每个结点都有一个从 0 到 25 的值,分别代表字母 ‘a’ 到 ‘z’:值 0 代表 ‘a’,值 1 代表 ‘b’,依此类推。
找出按字典序最小的字符串,该字符串从这棵树的一个叶结点开始,到根结点结束。
(小贴士:字符串中任何较短的前缀在字典序上都是较小的:例如,在字典序上 “ab” 比 “aba” 要小。叶结点是指没有子结点的结点。)
示例 1:

输入:[0,1,2,3,4,3,4]
输出:“dba”
示例 2:
输入:[25,1,3,1,3,0,2]
输出:“adz”
示例 3:

输入:[2,2,1,null,1,0,null,0]
输出:“abc”
思路:
前序遍历,使用StringBuilder累积当前路径,当到达叶子节点时,将路径翻转并和储存的之前的最小路径比较,然后在翻转回来,路径回退时除去当前添加的字符。注意体中的字典序比较直接使用字符串的compareTo即可,因为它默认使用字典序排序。最小路径的字符串用“~”初始化,因为其ASCII码为126,大于z。
代码:
class Solution {
String s = "~";
public String smallestFromLeaf(TreeNode root) {
if(root == null) return "";
StringBuilder sb = new StringBuilder();
helper(root,sb);
return s;
}
private void helper(TreeNode root,StringBuilder sb){
if(root == null) return;
sb.append((char)(root.val+'a'));
if(root.left == null && root.right == null){
//保留当前结果
String nowStr = sb.reverse().toString();
//还原
sb.reverse();
//比较当前结果和之前保留结果谁更优
if(nowStr.compareTo(s) < 0){
s = nowStr;
}
}
helper(root.left,sb);
helper(root.right,sb);
//路径回退时除去当前添加的字符
sb.deleteCharAt(sb.length()-1);
}
}
993. 二叉树的堂兄弟节点
在二叉树中,根节点位于深度 0 处,每个深度为 k 的节点的子节点位于深度 k+1 处。
如果二叉树的两个节点深度相同,但父节点不同,则它们是一对堂兄弟节点。
我们给出了具有唯一值的二叉树的根节点 root,以及树中两个不同节点的值 x 和 y。
只有与值 x 和 y 对应的节点是堂兄弟节点时,才返回 true。否则,返回 false。
示例 1:
输入:root = [1,2,3,4], x = 4, y = 3
输出:false
思路:
判断两个节点是否是堂兄弟节点就是判断他们是否在同一层并是否具有同一个父节点,我们可以构造两个哈希表,前序遍历添加节点的对应的父节点和深度,然后再从哈希表中取节点比较即可。
代码:
class Solution {
//同一深度和不同父节点则为堂兄弟节点
Map parentMap = new HashMap<>();//用来保存节点对应的父节点
Map depthMap = new HashMap<>();//用来保存节点对应的深度
public boolean isCousins(TreeNode root, int x, int y) {
if(root == null) return false;
helper(root,0,0);
//从两个Map中获得x/y
return (depthMap.get(x) == depthMap.get(y)) && (parentMap.get(x) != parentMap.get(y));
}
//前序遍历
private void helper(TreeNode root,int parent,int depth){
if(root == null) return;
//获取深度和父节点
parentMap.put(root.val,parent);
depthMap.put(root.val,depth);
helper(root.left,root.val,depth+1);
helper(root.right,root.val,depth+1);
}
}
1008. 先序遍历构造二叉树
返回与给定先序遍历 preorder 相匹配的二叉搜索树(binary search tree)的根结点。
示例:
输入:[8,5,1,7,10,12]
输出:[8,5,10,1,7,null,12]
思路:
先序遍历的结果为[根节点,左子树,右子树],因为是要构造BST,所以在先序结果中遍历找到比根节点大的第一个元素,为右子树根节点,其左边为左子树元素,右边为右子树元素,递归。
注意:如果没有比根节点大的元素,就只需要构造左子树,将分解索引定义为arr.length()+1,这样就不会越界。
代码:
class Solution {
public TreeNode bstFromPreorder(int[] arr) {
if(arr.length == 0) return null;
return helper(arr,0,arr.length-1);
}
private TreeNode helper(int[] arr,int lo,int hi){
if(lo > hi) return null;
//生成根节点
TreeNode root = new TreeNode(arr[lo]);
//遍历,求出右子树节点索引
int index = hi+1;//防止[4,2]越界
for(int i = lo+1;i <= hi;i++){
if(arr[i] > arr[lo]){
index = i;
break;
}
}
root.left = helper(arr,lo+1,index-1);
root.right = helper(arr,index,hi);
return root;
}
}
1022. 从根到叶的二进制数之和
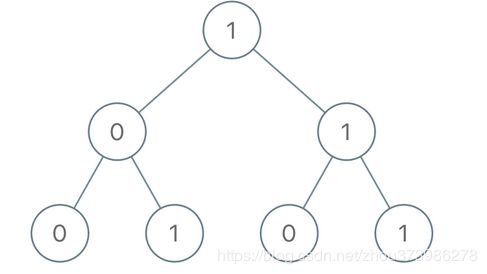
给出一棵二叉树,其上每个结点的值都是 0 或 1 。每一条从根到叶的路径都代表一个从最高有效位开始的二进制数。例如,如果路径为 0 -> 1 -> 1 -> 0 -> 1,那么它表示二进制数 01101,也就是 13 。
对树上的每一片叶子,我们都要找出从根到该叶子的路径所表示的数字。
输入:[1,0,1,0,1,0,1]
输出:22
解释:(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22
思路:
使用递归法:
当前节点的累加和 = 上层节点的累加和 * 2 + 当前节点值;
递归终止条件:当到达叶子节点时,将根到叶子节点的累加值加入sum中。 最终结果保存在sum中。
类似于题129
代码:
class Solution {
private int sum = 0;
public int sumRootToLeaf(TreeNode root) {
if(root == null) return 0;
getSum(root,0);
return sum;
}
private void getSum(TreeNode root,int val){
if(root == null) return;
if(root.left == null && root.right == null){
sum += val * 2 + root.val;
}
getSum(root.left,val * 2 + root.val);
getSum(root.right,val * 2+ root.val);
}
}