贝塞尔曲线后续

有关贝塞尔曲线的定义以及公式已经写在了上一篇文章中,这篇文章主要介绍这个曲线的应用

通过贝塞尔公式结算得到一个路径数组，结合dotween的DoPath做曲线动画

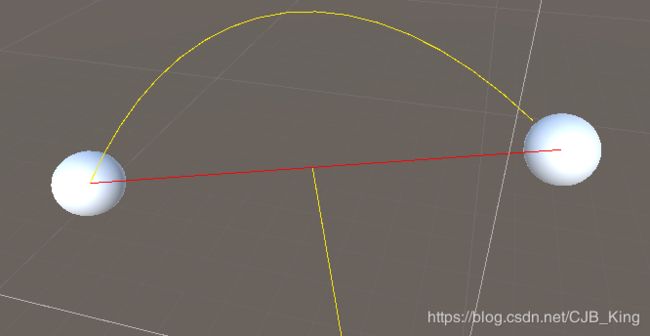
测试代码如下：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Vproject : MonoBehaviour
{
    public Transform start;
    public Transform end;
    public float ef = 1;
    public int vertCount = 3;
    public int pointCount = 10;     //曲线上点的个数
    private Vector3[] linePointList;
    void Start()
    {
        List<Vector3> newP = new List<Vector3>();
    }

    // Update is called once per frame
    void Update()
    {

    }
    public void OnDrawGizmos()
    {
        Vector3 center = (start.position + end.position) / 2;
        Vector3 centerProject = Vector3.Project(center, start.position - end.position);
        transform.position= Vector3.MoveTowards(center, centerProject, ef);
        Debug.DrawLine(center, centerProject,Color.yellow);
        Debug.DrawLine(start.position,end.position,Color.red);
        linePointList = BezierUtils.GetBeizerPointList(start.position, transform.position, end.position, vertCount);
        for (int i = 0; i < linePointList.Length - 1; i++)
        {
            Debug.DrawLine(linePointList[i], linePointList[i + 1], Color.yellow);
        }
    }
}

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public static class BezierUtils
{
    /// 

    /// 线性
    /// 
    /// 起点
    /// 终点
    /// 【0-1】
    /// 
    public static Vector3 BezierPoint(Vector3 p0, Vector3 p1, float t)
    {
        return (1 - t) * p0 + t * p1;
    }

    /// 

    /// 二阶曲线
    /// 
    /// 
    /// 
    /// 
    /// 
    /// 
    public static Vector3 BezierPoint(Vector3 p0, Vector3 p1, Vector3 p2, float t)
    {
        Vector3 p0p1 = (1 - t) * p0 + t * p1;
        Vector3 p1p2 = (1 - t) * p1 + t * p2;
        Vector3 result = (1 - t) * p0p1 + t * p1p2;
        return result;
    }

    /// 

    /// 三阶曲线
    /// 
    /// 
    /// 
    /// 
    /// 
    /// 
    /// 
    public static Vector3 BezierPoint(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, float t)
    {
        Vector3 result;
        Vector3 p0p1 = (1 - t) * p0 + t * p1;
        Vector3 p1p2 = (1 - t) * p1 + t * p2;
        Vector3 p2p3 = (1 - t) * p2 + t * p3;
        Vector3 p0p1p2 = (1 - t) * p0p1 + t * p1p2;
        Vector3 p1p2p3 = (1 - t) * p1p2 + t * p2p3;
        result = (1 - t) * p0p1p2 + t * p1p2p3;
        return result;
    }

    /// 

    /// 多阶曲线  （可以递归 有多组线性组合）
    /// 
    /// 
    /// 
    /// 
    public static Vector3 BezierPoint(float t, List<Vector3> p)
    {
        if (p.Count < 2)
            return p[0];
        List<Vector3> newP = new List<Vector3>();
        for (int i = 0; i < p.Count - 1; i++)
        {
            Vector3 p0p1 = (1 - t) * p[i] + t * p[i + 1];
            newP.Add(p0p1);
        }
        return BezierPoint(t, newP);
    }

    /// 

    /// 获取存储贝塞尔曲线点的数组(二阶)
    /// 
    /// 起始点
    /// 控制点
    /// 目标点
    /// 采样点的数量
    /// 存储贝塞尔曲线点的数组
    public static Vector3[] GetBeizerPointList(Vector3 startPoint, Vector3 controlPoint, Vector3 endPoint, int segmentNum)
    {
        Vector3[] path = new Vector3[segmentNum];
        for (int i = 1; i <= segmentNum; i++)
        {
            float t = i / (float)segmentNum;
            Vector3 pixel = BezierPoint(startPoint, controlPoint, endPoint, t);
            path[i - 1] = pixel;
        }
        return path;
    }

    /// 

    /// 获取存储贝塞尔曲线点的数组(多阶)
    /// 
    /// 采样点的数量
    /// 控制点集合
    /// 
    public static Vector3[] GetBeizerPointList(int segmentNum, List<Vector3> p)
    {
        Vector3[] path = new Vector3[segmentNum];
        for (int i = 1; i <= segmentNum; i++)
        {
            float t = i / (float)segmentNum;
            Vector3 pixel = BezierPoint(t, p);
            path[i - 1] = pixel;
        }
        return path;
    }

}