相关性分析
相关性分析 什么时候用?
相关分析 是研究两个或两个以上处于同等地位的随机变量间的相关关系的统计分析方法,其主体是对总体中具有因果关系标志的分析,它是描述客观事物相互间关系的密切程度并用适当的统计指标表示出来的过程
相关性分析 非常适合在题目要求分析两组数据之间的关系时使用
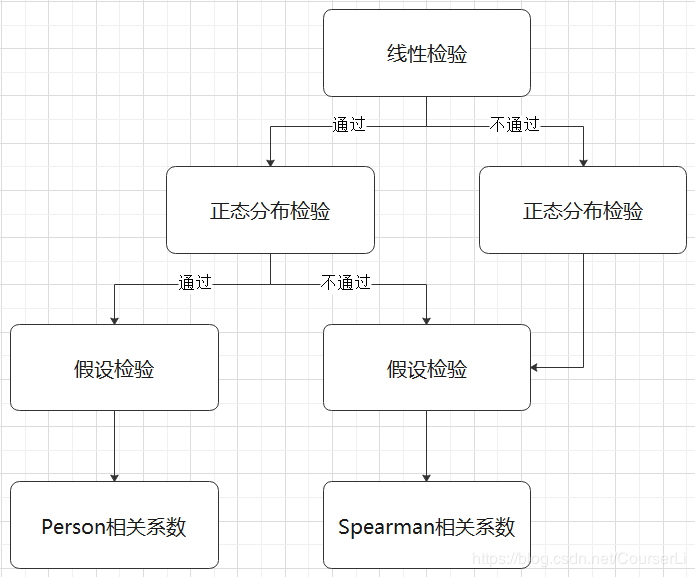
相关性分析的顺序
① 数据的描述性统计(求出各项指标)
② 线性关系检验(判断是否能用 Pearson)
③ 正态分布检验(判断是否能用 Pearson)
④ 确定相关性系数(Pearson 或 Spearman)
⑤ 相关性系数检验(得出结果)
相关性分析的例题演示
给出男生体测数据(共730行),分析男生体测数据各指标之间的相关性

一、数据的描述性统计
为分析男生体测成绩中各项指标的相关系数,首先用 SPSS 对数据中的各项指标做描述性统计,进行整体分析,结果如下图所示:
【操作步骤: 将 Excel 数据导入 SPSS 中,再进行如下操作,可得到描述统计的表格】

【操作步骤: 将此表格以 Excel 的 xlsx 格式导出,并对其进行数据调整,然后转换成 csv 格式,导入 Latex table 中,得到的公式粘贴到 Latex 中即可得到下表(表格可能不是很好看,到时候考虑是否要换成图片)】
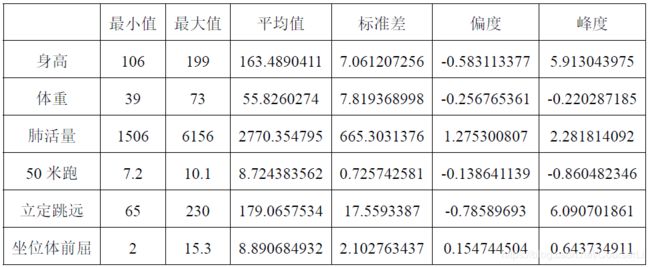
从上表我们可以得出男生体测成绩的各项指标的 最大值、最小值、平均值、标准差以及偏度和峰度
二、确定相关性系数
一般采用 皮尔逊 (Pearson)相关系数 或 斯皮尔曼 (Spearman)相关系数 来分析两个变量之间的相关系数,只有当两个变量之间呈线性关系时,才可以使用皮尔逊 (Pearson)相关系数,并且两变量呈正态分布时,才可以对皮尔逊 (Pearson)相关系数进行假设检验。因此,应先进行线性关系检验和正态分布检验,从而确定相关系数使用的类型
三、线性关系检验
为判断各项指标之间是否存在线性关系,应对各指标数据绘制散点图。将数据导入SPSS中,绘制散点图如下:
【操作: 图形‐ 旧对话框‐ 散点图/点图‐ 矩阵散点图;以 png 格式导出】
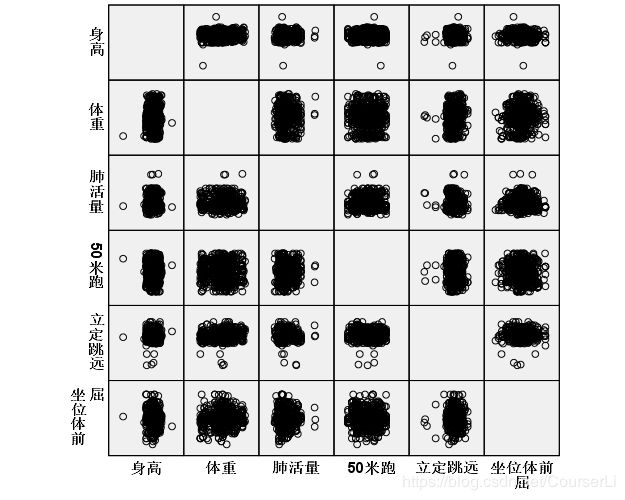
分析如上散点图可知,男生体测各项指标之间无显著的线性关系
三、正态分布检验
由于本题数据的样本容量 n = 730 n= 730 n=730,属于大样本容量,应采用 JB 检验(Jarque‐Bera test) 的方式检验各指标数据是否服从正态分布,下面进行假设检验:
原假设 H 0 H_0 H0:各指标都服从正态分布
备择假设 H 1 H_1 H1:各指标都不服从正态分布
接着,我们将通过 MATLAB 的 jbtest 函数对各指标数据进行求解,在 95% 的置信水平(即显著水平 a = 0.05 a=0.05 a=0.05)下,各指标数据的正态分布检验结果如下表所示:
| 指标 | h h h | p p p |
|---|---|---|
| 身高 | 1 | 0.0110 |
| 体重 | 1 | 0.0010 |
| 肺活量 | 1 | 0.0136 |
| 50米跑 | 1 | 0.0010 |
| 立定跳远 | 1 | 0.0010 |
| 坐位体前屈 | 1 | 0.0393 |
注:MATLAB 规定 p p p 返回值至少为 0.001,不足者返回 0.001
由上表可知,经正态分布检验之后,各指标的 h h h 值均为 1 且 p p p 值均小于 0. 05,即拒绝原假设,经散点图与正态分布检验分析可知,本题不能使用皮尔逊 (Pearson)相关系数分析,故考虑使用斯皮尔曼(Spearman) 相关系数
%% 正态分布检验
% 提前导入 Excel 数据并以 mat 保存
n_c = size(Test,2); % Test 为 Excel 中的数据
H = zeros(1,6);
P = zeros(1,6);
for i = 1 : n_c
[h,p] = jbtest(Test(:,i),0.05);
H(i)=h;
P(i)=p;
end
disp(H) % 1 1 1 1 1 1
disp(P) % 0.0110 0.0010 0.0136 0.0010 0.0010 0.0393
四、斯皮尔曼(Spearman) 相关系数
我们通过 SPSS 软件求解斯皮尔曼相关系数,运用显著性检验(即假设检验),对各指标数据进行相关性系数检验,最终结果如下表所示:
【操作: 将 Excel 数据导入 SPSS 中,再进行如下操作,可得到斯皮尔曼相关系数的表格】
【操作步骤: 将此表格以 Excel 的 xlsx 格式导出,并对其进行数据调整,然后转换成 csv 格式,导入 Latex table 中,得到的公式粘贴到 Latex 中即可得到下表(表格可能不是很好看,到时候考虑是否要换成图片)】
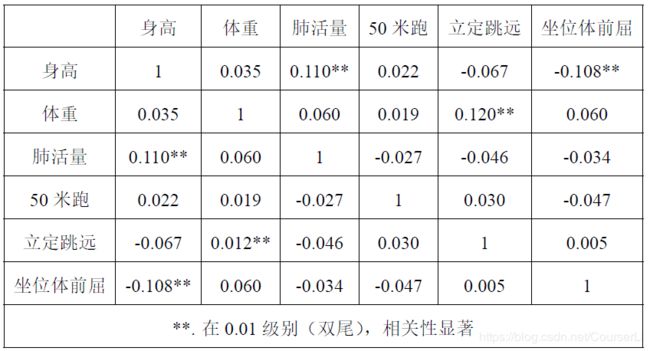
或者,可以用 矩阵热力图 代替上图(自动生成图表的网址:图标秀),颜色越深代表相关性越显著

由上表可知,男生体测数据中,总体看来,当显著水平 a = 0.05 a=0.05 a=0.05 时,身高与肺活量、体重与立定跳远存在着显著的正相关性,身高与坐位体前屈存在着显著的负相关性
相关性分析的补充
① 假设检验 就是一种方法
这个概念一开始绕了我很久,其实 假设检验 就是 显著性检验,它就是一种辅佐的方法,它可以辅佐检验正态分布,也可以辅佐检验相关性系数
原假设:… 备择假设:…(这就是假设检验)
注意:仅当数据没有通过线性检验时,才不能用假设检验辅佐 检验 Person 相关性系数,但可以用假设检验辅佐 检验 Spearman 相关性系数
② 正态分布 的小样本检验
例题中 正态分布 是用的是 JB 检验(Jarque‐Bera test),即大样本检验( 30 ⩽ n 30 ⩽ n 30⩽n)
而对于小样本检验( 3 ⩽ n ⩽ 50 3 ⩽ n ⩽50 3⩽n⩽50),我们应采取 夏皮洛-威尔克 检验(Shapiro-wilk),也称 W 检验
【操作步骤: 进行如下操作,可得到正态性检验表格】
下面的表格即正态性检验表格,而我们只需要右半部分
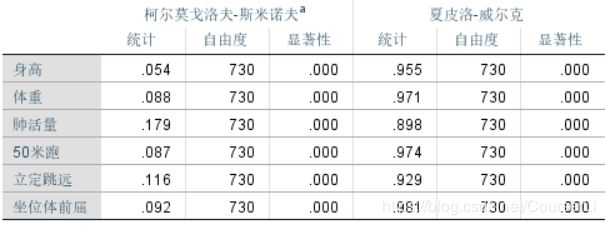
从图中看出,每个指标的显著性均小于 0. 05,各指标都不服从正态分布,即拒绝原假设,因此本题不能使用皮尔逊 (Pearson)相关系数分析 (又说了一次)
③ 斯皮尔曼(Spearman) 相关系数的第二种方法
例题中用到是第一种方法,可以直接用 SPSS 软件算相关系数,下面介绍第二种(MATLAB):
斯皮尔曼相关系数是衡量两变量间相关程度的非参数指标,运用斯皮尔曼相关系数时,原始数据依据其在总体数据中平均的降序位置,被分配了一个相应的等级,对于样本容量为 n n n 的样本, n n n 个原始数据被转化为等级数据 X i X_i Xi 和 Y i Y_i Yi,而 d i d_i di 为 X i X_i Xi 和 Y i Y_i Yi之间的等级差,利用同组数据的等级差计算得到斯皮尔曼相关系数,其计算公式为:
r s = 1 − 6 ∑ i = 1 n d i 2 n ( n 2 − 1 ) r_{s}=1-\frac{6 \sum_{i=1}^{n} d_{i}^{2}}{n\left(n^{2}-1\right)} rs=1−n(n2−1)6∑i=1ndi2
得到两组变量间的斯皮尔曼相关系数后,须对其进行相关性系数检验。大样本情况下,在原假设 r s = 0 r_s= 0 rs=0 的条件下,统计量 r s n − 1 ∼ N ( 0 , 1 ) r_{s} \sqrt{n-1} \sim N(0,1) rsn−1∼N(0,1) ,计算检验值 r s n − 1 r_{s} \sqrt{n-1} rsn−1 ,并求出相应的 p p p 值,与显著性水平 a a a 相比,即可得到显著性检验的结果
④ 斯皮尔曼(Spearman) 相关性系数检验的第二种方法
例题中用到是第一种方法,即适用于大样本( 30 ⩽ n 30 ⩽ n 30⩽n)的,而对于小样本( 3 ⩽ n ⩽ 50 3 ⩽ n ⩽50 3⩽n⩽50)下面介绍第二种方法 :查临界值表(双尾)
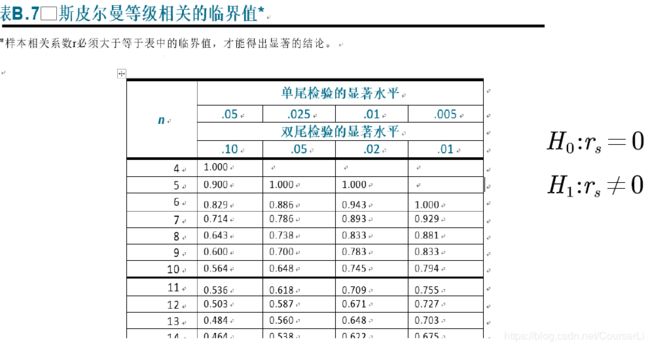
⑤ 补充例题中没讲的 皮尔逊 (Person)相关系数 求解
首先,讲讲 皮尔逊相关系数假设检验的条件,数据除了要通过线性检验之外,最好还要满足以下两点:
- 实验数据之间的差距不能太大
- 每组样本之间是独立抽样的
然后,Person 与 Spearman 的 相关系数求法 一样,都是用 SPSS 软件,如下图所示:


两个定序测量数据之间也只能用 Pearson 相关系数,不能用 Spearman 相关系数
直接举个简单的例子:
如前后两次考试成绩的相关就适合用 Pearson 相关
【前者通常是用来计算等距及等比数据或者说连续数据之间的相关的,不局限于整数】
如第一名和第二名的分数差就未必等于第二名和第三名的分数差,两次考试的每次各自的排名数据适用于 Spearman 相关
【后者专门用于计算等级数据之间的关系,数据有先后等级之分但连续两个等级之间的具体分数差异却未必相等】
⑦ 相关性分析 只是一种方法
相关性分析只是一种方法,而 皮尔逊 (Pearson)相关系数模型 和 斯皮尔曼 (Spearman)相关系数模型 才是模型,写论文的时候要注意点
相关性分析的评估
皮尔逊 (Pearson)相关系数模型 的优点:
效率更高
斯皮尔曼 (Spearman)相关系数模型 的优点
适用范围广
皮尔逊 (Pearson)相关系数模型 的缺点:
连续数据,正态分布,线性关系,且分析非两个定序数据之间的关系时,才能用使用,局限性较大
斯皮尔曼 (Spearman)相关系数模型 的缺点
效率较低