《Mastering the game of Go with deep neural networks and tree search》

1. 围棋问题在人工智能界之所以难以解决的问题所在？

• 围棋的棋盘位置较多，导致在走棋时搜索空间巨大
• 对于当前棋盘分布和下一步落子优劣性衡量具有一定难度

2. AlphaGo的技术解决方案和核心的算法思想

使用值网络来评估棋盘的布局，以及使用策略网络来选择每一次落子。这些深度神经网络在基于人类棋手的比赛的数据，通过对有监督学习的一种新的组合和自我对弈的强化学习来实现的。不使用前向搜索，而是使用蒙特卡洛搜索树进行成千上万次随机自我对弈的模拟游戏，同样引入了一种结合了蒙特卡洛树和策略网络、值网络的新的算法。

3. 引言部分

如何在评判当前是否是一种最优的分布或者此次落子后对于棋局的发展是否是最优的呢？这里使用的是一个全局的最优估值函数v*(s)，当我们要解决时就在搜索树中递归的调用这个函数。此时搜索树大约包含bd中走棋序列（b是每一次下棋的合法落子数，d是走棋的总共的步数长度），在围棋中，b≈250，d≈150，这样来看搜索的走棋序列是很大的，暴力的穷举搜索显然是不太具有可行性的，所以就需要想办法来减小搜索的有效空间：
• 通过对于棋局的衡量降低搜索的深度：在状态 s 时对搜索树进行剪枝，然后用一个近似估值函数v(s)来代替v(s) ，从而取代状态 s 下面的子树，通过这个近似估值函数预测状态 s 之后的对弈结果。
• 通过基于概率分布p(a∣s) 的策略的采样动作来降低搜索的深度：计算在某一位置 s 时，下一步落子为 a 的概率分布。比如蒙特卡洛走子方法搜索到最大深度时候根本不使用分歧界定法，它从一个策略 p 中采集双方棋手的一系列下棋走法。计算这些走子的平均数可以产生一个有效的棋局评估。

蒙特卡洛树搜索使用蒙特卡洛走子方法，来评估搜索树中每一个状态的估值，随着执行越来越多的模拟，搜索树变的越来越大，同时相关的估值也愈发精确。选择下棋动作的策略在搜索的过程中也会随着时间的推移而改进，通过选择拥有更高估值的子树。逐渐地，这个策略收敛到一个最优的下法，而且评估也会收敛到最优估值函数。目前最强的围棋程序是基于蒙特卡洛树搜索的，并且受到了策略（被人训练用来预测专家棋手的下法）的增强，这些策略被用来缩窄搜索空间到一束高可能性下棋动作，同时在走子中进行采样。先前的工作已经受到了浮于表面策略或基于输入特征线性组合的估值函数的限制。

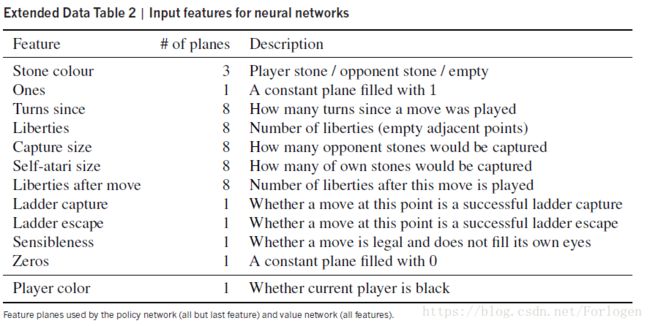
深度卷积神经网络已经在计算机视觉中达到了空前的性能：比如图像分类，人脸识别，和玩雅达利的游戏，它使用很多层的神经网络，层与层之间重叠排列在一起，用来构建关于图像的的愈发抽象的、局部性的代表。在AlphaGo中采用了类似的体系架构，将棋局分布作为一个19*19的图像输入，然后使用卷积神经网络来构建一个位置的代表。通过使用神经网络来降低搜索树的有效的深度和广度：通过估值网络来评估棋局，和使用策略网络来博弈取样。

使用一个包含多个不同阶段的机器学习方法的管道来训练神经网络，创建的神经网络主要有如下几个：
• 有监督学习（supervised learning，SL）的策略网络pσ：直接来自于人类专家的下棋资料，通过快速的反馈机制和高质量的梯度实现学习算法的快速高效的更新
• 从快速走子中采样的快速网络pπ：
• 强化学习（reinforcement learning，RL）的策略网络pρ：通过自我对弈最终结果的优化来提升pσ的性能，使策略网络朝着最终赢棋的目标前进，而不只是最大化的提高预测精度
• 估值网络vθ：通过RL策略网络的自我对弈来预测博弈的赢家
AlphaGo程序有效的把策略网络、估值网络和蒙特卡洛搜索树结合在一起。

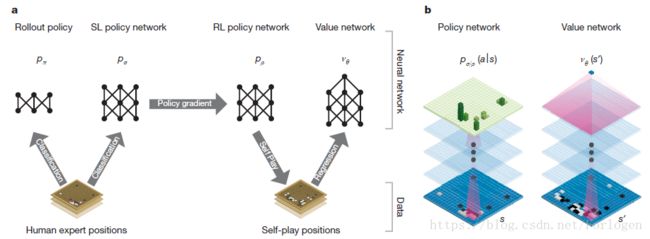
4. 监督学习的策略网络

在训练管道的第一阶段，基于先前工作使用了监督学习来预测人类专家下围棋。监督学习的策略网络pσ(a | s) 在权重σ的卷积层和非线性的修正器中替换，最后的softmax层输出所有可能合法的走子a的概率分布。
策略网络的输入 s 是当前棋局分布的代表

策略网络使用了随机取样状态-动作对（s，a）进行训练，使用了随机梯度上升来最大化模拟人类在状态 s 选择下棋走子 a 的可能性。使用随机梯度上升来更新权重参数

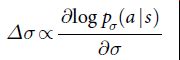
用KGS围棋服务器的3千万个棋局，训练了13层的策略网络（我们称之为SL 策略网络）。在输入留存测试数据的所有特征后，网络预测人类专家下棋的精准度的达到了57%；在仅仅使用原始棋局和下棋记录的时候，精度达到了55.7%。与之相比，截至到本篇文论提交（2015年），其他研究团队的最先进的精度是44.4%。

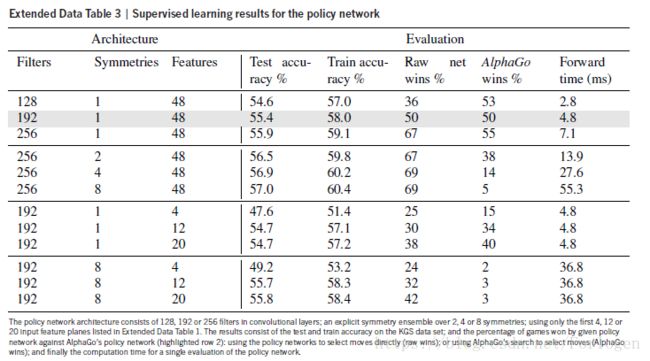
在精确度方面的小提升会引起下棋能力的很大提升（从图中可以看出，精确的越高，胜率就会越高，同时显示了在不同复杂度的网络下的情况）

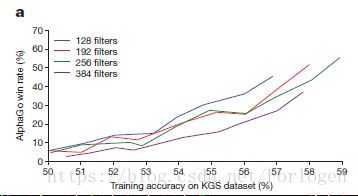
显示了策略网络的下棋能力随着它们的训练精确度的函数。拥有128，192，256，384卷积过滤每层的策略网络在训练过程中得到周期性的评估；这个图显示了AlphaGo使用不同策略网络的赢棋概率随着的不同精确度版本的AlphaGo的变化。

更大的神经网络拥有更高的精确度，但是在搜索过程中评估速度更慢。同时训练了一个更快的但是精确度更低的走子策略pπ(a|s) ，它使用了一个权重为π 的小型模式特征的线性softmax，达到了24.2%的精确度，每选择下一步棋只用2微秒，与之相比，策略网络需要3毫秒。

5. 强化学习的策略网络

训练管道第二阶段的目标是通过策略梯度强化学习（RL）来提高策略网络。强化学习策略网络pρ 在结构上和 监督学习的策略网络是一样的，权重ρ 初始值也是一样的ρ = σ。我们在当前的策略网络pρ和随机选择某先前一次迭代的策略网络之间博弈。从一个对手的候选池中随机选择，可以基于当前的策略网络稳定训练过程，同时防止过度拟合。我们使用一个奖励函数 r(s)，对于所有非终端的步骤 t < T，它的值等于零。从当前棋手在步骤 t 的角度来讲，结果 zt = ± r(sT)是在博弈结束时候的终端奖励，如果赢棋，结果等于 +1，如果输棋，结果等于 -1。然后权重在每步 t使用随机梯度上升进行 更新，朝着最大化预期结果的方向前进

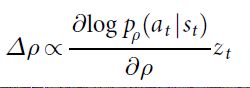
在博弈过程中评估 RL策略网络的性能表现，从输出的下棋动作的概率分布，对每一下棋动作at∼pρ(⋅∣st) 进行取样。我们自己面对面博弈，RL策略网络对 SL策略网络的胜率高于80%。我们也测试了和最强的开源围棋软件 Pachi （一个随机的蒙特卡洛搜索程序）对弈，在每一步落子时进行100000次模拟，在KGS中达到业余2段。在没有使用任何搜索的情况下，RL策略网络对 Pachi的胜率达到了85%。与之相比，之前的最先进的仅仅基于监督学习的卷积网络，对 Pachi的胜率仅只有11%，对稍弱的程序 Fuego的胜率是12%。

6. 强化学习的值网络

训练管道的最后一个阶段关注于棋局评估，评估一个估值函数 vp(s) ，它预测从棋局状态 s 开始，博弈双方都按照策略网络 p 下棋的结局，

理想情况下，我们期望知道在完美下法v*(s)情况下的最优值；然而在现实中，我们使用 RL策略网络pρ，来评估估值函数v pρ ，作为我们的最佳策略。我们使用权重是θ 的估值网络vθ(s)来逼近估值函数，vθ(s)≈vPp≈v*(s)。这个神经网络和策略网络拥有近似的体系结构，但是输出是一个单一的预测，而不是一个概率分布。我们通过回归到状态-结果对（s, z）来训练估值网络的权重，使用随机梯度下降来最小化预测估值vθ(s)和相应的结局 z 之间的均方误差（MSE）。

这个从完整对弈的数据来预测博弈结局的朴素的方法导致过度拟合。问题在连续的棋局之间是强相关的，不仅与单独下一步棋不同，而且回归目标和整个博弈又是相通的。当通过这种方式在KGS数据集合上训练时，估值网络记住了博弈的结局而不是泛化出新的棋局，在测试数据上面MSE最小达到了0.37，与之相比在训练数据集合上面MSE是0.19。为了解决这个问题，想出了新的自我对弈的数据集合，包含了三千万个不同的棋局，每一个都是从不同盘博弈中采样。每一盘博弈都是在 RL策略网络和自己之间对弈，直到博弈结束。在这个数据集合上训练导致了MSE为0.226，和训练和测试数据集合的MSE为0.234，这显示此时只有很小的过拟合。

b：估值网络和不同策略网络的评估对比。棋局和结局是从人类专家博弈对局中采样的。每一个棋局都是由一个单独的向前传递的估值网络vθ 评估的，或者100个走子的平均值，这些走子是由统一随机走子，或快速走子策略pπ ，或 SL 策略网络pδ ，或 RL 策略网络pρ 。图中，预测估值和博弈实际结局之间的平均方差随着博弈的进行阶段（博弈总共下了多少步）的变化而变化。

上图显示了估值网络对棋局评估的精确度：对比使用了快速走子策略网络pπ 的蒙特卡洛走子的精确度，估值函数一直更加精确。一个单一的评估vθ(s) 的精确度也逼近了使用了 RL策略网络vθ(s)的蒙特卡洛走子的精确度，不过计算量是原来的15000分之一。

7. 基于策略网络和值网络的搜索

AlphaGo在蒙特卡洛搜索中结合和策略网络和值网络，通过前瞻性搜索来选择动作。搜索树的每一边（s，a）存储着一个动作值 Q(s, a)、访问计数 N(s, a)和先验概率 P(s, a)。这棵树从根节点开始，通过模拟来遍历（比如在完整的博弈中沿着树无备份地向下搜索）。在每次模拟的每一步 t，根据状态 s来选择一个下棋动作at 。

给最大化动作估值加上一个额外奖励，

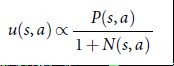
它和先验概率成正比，与访问次数成反比。当在步骤 L 遍历到达一个叶节点sL 时，该叶节点可能不会被扩展。叶节点棋局sL 仅被 SL策略网络pσ执行一次。输出的概率存储下来作为每一合法下法 a 的先验概率 P

叶节点通过两种方式的得到评估：
• 通过价值网络vθ(sL)评估；
• 用快速走子策略pπ 随机走子，直到终点步骤 T，产生的结果zL作为评估方法。这些评估方法结合在一起，在叶节点的评估函数V(sL)中使用一个混合参数λ

在模拟的结尾，更新所有被遍历过的边的下棋动作估值和访问次数：每一条边累加访问次数，求出所有经过该边的模拟估值的平均值。

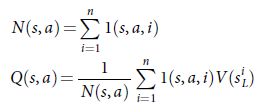
其中siL是第 i 次模拟的叶节点，1(s, a, i)代表一条边 (s, a) 在第 i 次模拟时是否被遍历过。一旦搜索完成，算法选择从根节点开始被访问次数最多的节点。

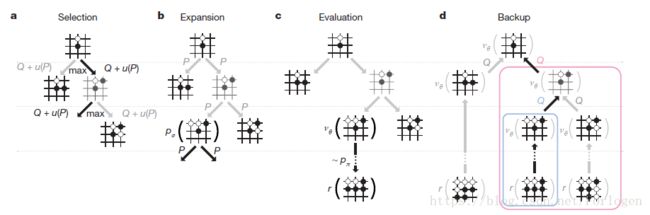
AlphaGo中的蒙特卡洛树搜索。a 每一次模拟遍历搜索树，通过选择拥有最大下棋动作估值 Q的边，加上一个额外奖励 u§（依赖于存储的该边的先验概率 P） 。b叶节点可能被展开，新的结点被策略网络pθ 执行一次，然后结果概率存储下来作为每一个下棋动作的先验概率。c在一次模拟的结尾，叶节点由两种方式评估：使用估值网络 vθ和运行一个走子策略直到博弈结尾（使用了快速走子策略pπ ），然后对于赢者运算函数 r。d 下棋动作估值 Q 得到更新，用来跟踪所有评估 r(.) 的平均值和该下棋动作的子树的vθ(⋅)

在AlphaGo中，SL策略网络pσ的表现优于 RL策略网络pρ ，可能是因为人类是从一束不同的前景很好的下棋走法中选择， RL是优化单一最优下棋走法。然而，从更强的 RL策略网络训练出来的估值函数vθ(s)≈v pρ(s) 优于从 SL策略网络训练出来的估值函数vθ(s)≈v pσ(s)。

评估策略网络和估值网络和传统的启发式搜索相比，需要多几个数量级的计算量。为了高效的把 MCTS 和深度神经网络结合在一起，AlphaGo 在很多CPU上使用异步多线程搜索技术进行了模拟，在很多GPU上计算策略网络和估值网络。最终版本的 AlphaGo使用了40个搜索线程，48个CPU，和8个GPU。我们也实现了一个分布式的AlphaGo版本，它利用了多台电脑，40个搜索线程，1202个CPU，176个GPU。

8. 评估AlphaGo的下棋能力

为了评估 AlphaGo 的水平，我们举办了内部比赛，成员包括不同版本的 Alph Go 和几个其它的围棋程序，包括最强的商业程序 CrazyStone和Zen，和最强的开源程序Pachi和Fuego。所有这些程序都是基于高性能蒙特卡洛树搜索算法的。此外，我们的内部比赛还包括了开源程序GnuGo，它使用了最先进搜索方法的蒙特卡洛树搜索。所有程序每次执行下一步棋允许5秒钟。

比赛的结果如下

AlphaGo的比赛评估。a 和不同围棋程序比赛的结果。每个程序使用接近5秒每走一步棋的速度。为了给AlphaGo更高的挑战难度，一些程序得到了所有对手让4步子的优势。程序的评估基于ELO体系：230分的差距，这相当于79%的胜率差距，这大致相当于在KGS中高一个业余等级。一个和人类接近的相当也显示了，水平的线显示了程序在在线比赛中达到的KSG等级。和欧洲冠军樊麾的比赛也包括在内。这些比赛使用更长的时间控制。图中显示了95%的置信区间。b 单机版本的AlphaGo在组成部分的不同组合下的性能表现。其中仅仅使用了策略网络的版本没有使用任何搜索算法。c 蒙特卡洛搜索树算法关于搜索线程和GPU的可扩展性研究，其中使用了异步搜索（浅蓝色）和分布式搜索（深蓝色），每下一步时间两秒。

比赛的结果显示了单机版本的AlphaGo比先前任何一个围棋程序强上很多段，在495场比赛中，AlphaGo赢了其中的494场比赛。我们也在让对手4目棋的情况下进行了比赛：AlphaGo和CrazyStone，Zen，Pachi的胜率分别是77%，86%，99%。分布式版本的AlphaGo强大很多：和单机版本的AlphaGo对弈的胜率是77%，和其他的围棋程序对弈的胜率是100%。

我们也评估了不同版本的AlphaGo，不同版本仅仅使用估值网络（λ=0 ）或者仅仅使用快速走子（λ=1 ）。即使不使用快速走子，AlphaGo的性能超出了所有其他围棋程序，显示了估值网络提供了一个可行的代替蒙特卡洛评估的可能。不过，其估值网络和快速走子的混合版本表现最好（λ=0.5），在对其他版本的AlphaGo的时候胜率达到了95%以上。这预示着这两种棋局评估系统是互补的：估值网络通过能力很强，但是不切实际的慢的pρ 来逼近博弈的结局；快速走子可以通过能力更弱但是更快的快速走子策略pρ 来精确的评估博弈的结局。

AlphaGo（执黑）是在一个和樊麾的非正式的比赛中选择下棋走子的。接下来的每一个统计中，估值最大的落子地点用橘黄色标记。a根节点 s 的所有后继结点 s’ 的估值，使用估值网络 vθ(s′) ，评估很靠前的会赢的百分数显示出来了。b 从根节点开始的每一条边(s, a)的走子动作估值 Q(s, a)；仅仅使用估值网络（λ=0 ）方法的均值。c 下棋动作 Q(s, a)，仅仅使用快速走子（λ=1 ）方法的均值。d 直接使用 SL策略网络的下棋走子概率，p σ(a|s)；如果大于0.1%的话，以百分比的形式报告出来。e 从根节点开始的模拟过程中下棋走子地点选择的频率百分比。f AlphaGo的树搜索的理论上的走子选择序列（一个搜索过程中访问次数最多的路径）。下棋走子用一个数字序列示。AlphaGo选择下棋的落子地点用红色圆圈标记出来；樊麾下在白色方形的地方作为回应；在他的复盘过程中，他评论道：下在地点 1 应该是更好的选择，而这个落子地点正好是AlphaGo预测的白棋的落子地点。

最终，我们把分布式版本的AlphaGo和樊麾进行了评估，他作为一个职业2段棋手，是2013，2014，2015年的欧洲围棋冠军。在2015年10月5-9日，AlphaGo和樊麾在真实比赛中下了5盘棋。AlphaGo以5：0的比分赢了比赛，这是史上第一次，在人类不让子和完整棋盘的情况下，一个围棋程序在赢了一个人类职业棋手，这个壮举之前认为需要至少十年才能达到。

AlphaGo 和欧洲冠军樊麾的博弈棋局。下棋走的每一步按照下棋顺序由数字序列显示出来。重复落子的地方在棋盘的下面成双成对显示出来。每一对数字中第一个数字的落子，重复下到了第二个数字显示的交叉地方。

9. 讨论

我们基于深度神经网络和蒙特卡洛搜索的结合开发了AlphaGo，同时与最高水平的人类棋手进行了对弈，解决了人工智能一个巨大的挑战。同样第一次为围棋游戏开发了有效的走子选择和棋局评估的函数，它基于深度神经网络，由监督学习和强化学习的一种新的组合来训练。同时引入了一种新的搜索算法，它成功的结合了神经网络评估和蒙特卡洛走子。AlphaGo将这些方法结合在一起，在树搜索中有着很高的性能。

AlphaGo相比于深蓝，它对于位置的选择更加的智能，策略网络使得评估更加精确，值网络使得下的方法更接近与人。它不依赖于人造的评估函数，基于神经网络的AlphaGo直接由监督学习和强化学习的通用目的来训练。

围棋是人工智能所面对的诸多困难中的一个典型：挑战性的决策的制定、巨大的搜索空间、复杂的最优下法。先前在围棋游戏中最大的突破就是蒙特卡洛搜索的引入，它在其他领域也会提供一种新的方法，比如游戏问题、经典规划问题、部分观察规划问题、调度问题和约束满足问题。结合了神经网络和树搜索的AlphaGo在围棋领域最终到达了一个专业的层次，它提供了一种希望，在人工智能的很多领域，同样可以达到优秀的人类水平的表现。

10. 参考文献

1. Allis, L. V. Searching for Solutions in Games and Artificial Intelligence. PhD thesis, Univ. Limburg, Maastricht, The Netherlands (1994).
2. van den Herik, H., Uiterwijk, J. W. & van Rijswijck, J. Games solved: now and inthe future. Artif. Intell. 134, 277–311 (2002).
3. Schaeffer, J. The games computers (and people) play. Advances in Computers 52, 189–266 (2000).
4. Campbell, M., Hoane, A. & Hsu, F. Deep Blue. Artif. Intell. 134, 57–83 (2002).
5. Schaeffer, J. et al. A world championship caliber checkers program. Artif. Intell. 53, 273–289 (1992).
6. Buro, M. From simple features to sophisticated evaluation functions. In 1st International Conference on Computers and Games, 126–145 (1999).
7. Müller, M. Computer Go. Artif. Intell. 134, 145–179 (2002).
8. Tesauro, G. & Galperin, G. On-line policy improvement using Monte-Carlo search. In Advances in Neural Information Processing, 1068–1074 (1996).
9. Sheppard, B. World-championship-caliber Scrabble. Artif. Intell. 134, 241–275 (2002).
10. Bouzy, B. & Helmstetter, B. Monte-Carlo Go developments. In 10th International Conference on Advances in Computer Games, 159–174 (2003).
11. Coulom, R. Efficient selectivity and backup operators in Monte-Carlo tree search. In 5th International Conference on Computers and Games, 72–83 (2006).
12. Kocsis, L. & Szepesvári, C. Bandit based Monte-Carlo planning. In 15th European Conference on Machine Learning, 282–293 (2006).
13. Coulom, R. Computing Elo ratings of move patterns in the game of Go. ICGA J. 30, 198–208 (2007).
14. Baudiš, P. & Gailly, J.-L. Pachi: State of the art open source Go program. In Advances in Computer Games, 24–38 (Springer, 2012).
15. Müller, M., Enzenberger, M., Arneson, B. & Segal, R. Fuego – an open-source framework for board games and Go engine based on Monte-Carlo tree search. IEEE Trans. Comput. Intell. AI in Games 2, 259–270 (2010).
16. Gelly, S. & Silver, D. Combining online and offline learning in UCT. In 17th International Conference on Machine Learning, 273–280 (2007).
17. Krizhevsky, A., Sutskever, I. & Hinton, G. ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems, 1097–1105 (2012).
18. Lawrence, S., Giles, C. L., Tsoi, A. C. & Back, A. D. Face recognition: a convolutional neural-network approach. IEEE Trans. Neural Netw. 8, 98–113 (1997).
19. Mnih, V. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015).
20. LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
21. Stern, D., Herbrich, R. & Graepel, T. Bayesian pattern ranking for move prediction in the game of Go. In International Conference of Machine Learning, 873–880 (2006).
22. Sutskever, I. & Nair, V. Mimicking Go experts with convolutional neural networks. In International Conference on Artificial Neural Networks, 101–110 (2008).
23. Maddison, C. J., Huang, A., Sutskever, I. & Silver, D. Move evaluation in Go using deep convolutional neural networks. 3rd International Conference on Learning Representations (2015).
24. Clark, C. & Storkey, A. J. Training deep convolutional neural networks to play go. In 32nd International Conference on Machine Learning, 1766–1774 (2015).
25. Williams, R. J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 8, 229–256 (1992).
26. Sutton, R., McAllester, D., Singh, S. & Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. In Advances in Neural Information Processing Systems, 1057–1063 (2000).
27. Sutton, R. & Barto, A. Reinforcement Learning: an Introduction (MIT Press, 1998).
28. Schraudolph, N. N., Dayan, P. & Sejnowski, T. J. Temporal difference learning of position evaluation in the game of Go. Adv. Neural Inf. Process. Syst. 6, 817–824 (1994).
29. Enzenberger, M. Evaluation in Go by a neural network using soft segmentation. In 10th Advances in Computer Games Conference, 97–108 (2003). 267.
30. Silver, D., Sutton, R. & Müller, M. Temporal-difference search in computer Go. Mach. Learn. 87, 183–219 (2012).
31. Levinovitz, A. The mystery of Go, the ancient game that computers still can’t win. Wired Magazine (2014).
32. Mechner, D. All Systems Go. The Sciences 38, 32–37 (1998).
33. Mandziuk, J. Computational intelligence in mind games. In Challenges for Computational Intelligence, 407–442 (2007).
34. Berliner, H. A chronology of computer chess and its literature. Artif. Intell. 10, 201–214 (1978).
35. Browne, C. et al. A survey of Monte-Carlo tree search methods. IEEE Trans. Comput. Intell. AI in Games 4, 1–43 (2012).
36. Gelly, S. et al. The grand challenge of computer Go: Monte Carlo tree search and extensions. Commun. ACM 55, 106–113 (2012).
37. Coulom, R. Whole-history rating: A Bayesian rating system for players of time-varying strength. In International Conference on Computers and Games, 113–124 (2008).
38. KGS. Rating system math. http://www.gokgs.com/help/rmath.html.