Python笔记：线性回归模型

《Python数据科学：技术详解与商业实践》线性回归案例

# 数据说明：本数据是一份汽车贷款数据

# |字段名|中文含义|
# |:--:|:--:|
# |id|id|
# |Acc|是否开卡(1=已开通)|
# |avg_exp|月均信用卡支出（元）|
# |avg_exp_ln|月均信用卡支出的自然对数|
# |gender|性别(男=1)|
# |Age|年龄|
# |Income|年收入（万元）|
# |Ownrent|是否自有住房（有=1；无=0)|
# |Selfempl|是否自谋职业(1=yes, 0=no)|
# |dist_home_val|所住小区房屋均价(万元)|
# |dist_avg_income|当地人均收入|
# |high_avg|高出当地平均收入|
# |edu_class|教育等级：小学及以下开通=0，中学=1，本科=2，研究生=3|

import matplotlib.pyplot as plt
import numpy as np
import  pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols
pd.set_option('display.max_columns',8)
r = pd.read_csv('数据科学数据\creditcard_exp.csv',skipinitialspace=True)
#筛选avg_exp非空数据进行建模，空数据进行预测
exp = r[r['avg_exp'].notnull()].copy().iloc[:,2:].drop('age2',axis=1)
exp_new=r[r['avg_exp'].isnull()].copy().iloc[:,2:].drop('age2',axis=1)
exp[['Income','Age','dist_home_val','avg_exp']].corr(method='pearson')#数据相关性分析

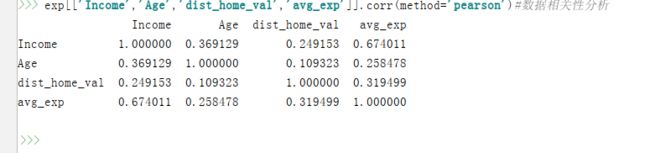
由图可以判断得出avg_exp与income有较大的关系，因此采用income对avg_exp进行模型构建

exp.plot('Income', 'avg_exp', kind='scatter')   #可视化
plt.show()

lms = ols('avg_exp~ Income',data=exp).fit()
print(lms.params)   #查看回归系数，截距项

这里采用ols返回一个模型（最小二乘法），模型用fit（）训练

lms = ols('avg_exp~ Income',data=exp).fit()
print(lms.params)   #查看回归系数，截距项
lms.summary()  #查看模型概括
pd.DataFrame([lms.predict(exp),lms.resid],index=['predict','resid']).T.head() #使用模型对训练集进行预测以及计算残差
lms.predict(exp_new)    #测试集进行预测

多元线性回归模型的预测

lm_s = ols('avg_exp ~ Income+dist_home_val+dist_avg_income+Age', data=exp).fit()
pd.DataFrame([lm_s.predict(exp),lm_s.resid],index=['predict','resid']).T.head()
lm_s.summary()

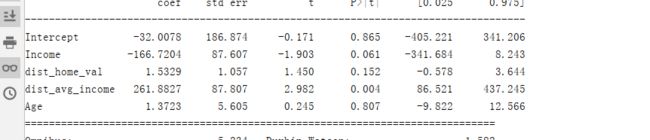
可以看出age，dist_home_val对模型的显著性较低，对于该方程，这里采用向前回归法对方程进行处理

def forward_select(data, response):
    remaining = set(data.columns)
    remaining.remove(response)
    selected = []
    current_score, best_new_score = float('inf'), float('inf')
    while remaining:
        aic_with_candidates = []
        for candidate in remaining:
            formula = "{} ~ {}".format(
                response, ' + '.join(selected + [candidate]))
            aic = ols(formula=formula, data=data).fit().aic
            aic_with_candidates.append((aic, candidate))
        aic_with_candidates.sort(reverse=True)
        best_new_score, best_candidate = aic_with_candidates.pop()
        if current_score > best_new_score:
            remaining.remove(best_candidate)
            selected.append(best_candidate)
            current_score = best_new_score
            print('aic is {},continuing!'.format(current_score))
        else:
            print('forward selection over!')
            break

    formula = "{} ~ {} ".format(response, ' + '.join(selected))
    print('final formula is {}'.format(formula))
    model = ols(formula=formula, data=data).fit()
    return (model)

data_for_select = exp[['avg_exp', 'Income', 'Age', 'dist_home_val',
                       'dist_avg_income']]
lm_m = forward_select(data=data_for_select, response='avg_exp')
print(lm_m.rsquared)
pd.DataFrame([lm_m.predict(exp),lm_m.resid],index=['predict','resid']).T.head() #使用模型对训练集进行预测以及计算残差
lm_m.predict(exp_new)

最终删除age，获得模型