k均值聚类算法原理和TensorFlow实现

1.原理简介

k均值聚类是一种对数据进行聚类的技术，即将数据分割成指定数量的几个类，揭示数据的内在性质及规律。k 均值聚类是一种无监督学习方法。聚类技术很多，例如层次法、贝叶斯法和划分法。k 均值聚类属于划分聚类方法，将数据分成 k 个簇，每个簇有一个中心，称为质心，k 值需要给定。k 均值聚类算法的工作原理如下：

1. 随机选择 k 个数据点作为初始质心（聚类中心）。
2. 将每个数据点划分给距离最近的质心，衡量两个样本数据点的距离有多种不同的方法，最常用的是欧氏距离。
3. 重新计算每个簇的质心作为新的聚类中心，使其总的平方距离达到最小。
4. 重复第 2 步和第 3 步，直到收敛。

2.代码实现

准备工作：

根据 TensorFlow 文档，KmeansClustering 类对象可以使用以下__init__方法进行实例化： 



TensorFlow 文档对这些参数的定义如下：

• num_clusters：要训练的簇数。
• model_dir：保存模型结果和日志文件的目录。
• initial_clusters：指定如何对簇初始化，取值请参阅 clustering_ops.kmeans。
• distance_metric：聚类的距离度量方式，取值请参阅 clustering_ops.kmeans。
• random_seed：Python 中的整数类型，用于初始化质心的伪随机序列发生器的种子。
• use_mini_batch：如果为 true，运行算法时分批处理数据，否则一次使用全部数据集。
• mini_batch_steps_per_iteration：经过指定步数后将计算的簇中心更新回原数据。更多详细信息参见 clustering_ops.py。
• kmeans_plus_plus_num_retries：对于在 kmeans++ 方法初始化过程中采样的每个点，该参数指定在选择最优值之前从当前分布中提取的附加点数。如果指定了负值，则使用试探法对 O(log(num_to_sample)) 个附加点进行抽样。
• relative_tolerance：相对误差，在每一轮迭代之间若损失函数的变化小于这个值则停止计算。有一点要注意就是，如果将 use_mini_batch 设置为 True，程序可能无法正常工作。

TensorFlow 支持将欧氏距离和余弦距离作为质心的度量，KmeansClustering 类提供了多种交互方法。在这里使用 fit()、clusters() 和 predict_clusters_idx() 方法：

根据 TensorFlow 文档描述，需要给 fit() 提供 input_fn() 函数，cluster 方法返回簇质心，predict_cluster_idx 方法返回得到簇的索引。

具体做法

这里使用鸢尾花卉数据集，该数据集分为三类，每类都是指一种鸢尾花卉，每类有 50 个实例。可以从https://archive.ics.uci.edu/ml/datasets/iris上下载 .csv 文件，也可以使用 sklearn 库的数据集模块（scikit-learn）来加载数据：

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import datasets

iris=datasets.load_iris()
x=iris.data[:,:2]  #only take the first teo features
y=iris.target

定义 input_fn 来给 fit() 方法输入数据，函数返回一个 TensorFlow 常量，用来指定x的值和维度，类型为 float：

def input_fn():
    return tf.constant(np.array(x),tf.float32,x.shape),None

开始使用 KmeansClustering 类，分为 3 类，设置 num_clusters=3。通常情况下事先并不知道最优的聚类数量，在这种情况下，常用的方法是采用肘部法则（elbow method）来估计聚类数量：

kmeans=tf.contrib.learn.KmeansClustering(num_clusters=3,relative_tolernence=0.0001,random_seed=2)
kmeans.fit(input_fn=input_fn)

使用 clusters() 方法找到这些簇，使用 predict_cluster_idx() 方法为每个输入点计算分配的簇索引：

cluster=kmeans.cluster()
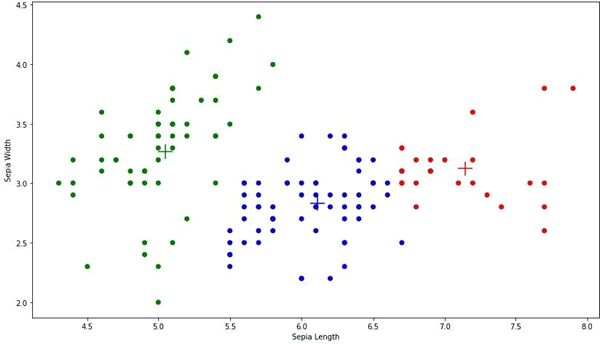
assignments=list(kmeans.predict_cluster_idx(input_fn=input_fn))

对创建的簇进行可视化操作，创建一个包装函数 ScatterPlot，它将每个点的 X 和 Y 值与每个数据点的簇和簇索引对应起来：

def ScatterPlot(X,Y,assignments=None,centers=None):
    if assignments is None:
        assignments=[0]*len(X)
        fig=plt.figure(figsize=(14,8))
        cmap=ListedColormap(['red','green','blue'])
        plt.scatter(X,Y,c=assignments,cmap=cmap)
        if centers is not None:
            plt.scatter(centers[:,0],centers[:,1],c=range(len(centers)),marker='+',s=400,cmap=cmap)
            plt.xlabel('Sepia Length')
            plt.ylabel('Sepia Width')    
            
ScatterPlot(X[:,0],x[:,1],assignments,clusters)

 

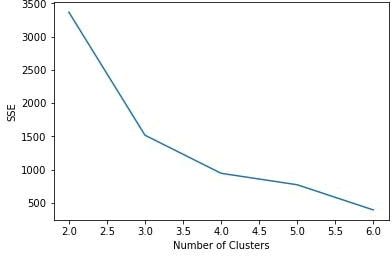
上面的案例中使用 TensorFlow Estimator 的 k 均值聚类进行了聚类，这里是提前知道簇的数目，因此设置 num_clusters=3。但是在大多数情况下，数据没有标签，我们也不知道有多少簇存在，这时候可以使用肘部法则确定簇的最佳数量,肘部法则选择簇数量的原则是减少距离的平方误差和（SSE），随着簇数量 k 的增加，SSE 是逐渐减小的,想要的是一个较小的 k 值，而且 SSE 也较小。在 TensorFlow 中，可以使用 KmeansClustering 类中定义的 score() 方法计算 SSE，该方法返回所有样本点距最近簇的距离之和：

sum_distances=kmeans.score(input_fn=input_fn,steps=100)

对于鸢尾花卉数据，如果针对不同的 k 值绘制 SSE，能够看到 k=3 时，SSE 的变化是最大的；之后变化趋势减小，因此肘部 k 值可设置为 3：

k 均值聚类因其简单、快速、强大而被广泛应用，当然它也有不足之处，最大的不足就是用户必须指定簇的数量；其次，算法不保证全局最优；再次，对异常值非常敏感。