数据结构与算法专题之线性表——栈及其应用
本文内容是数据结构第二弹——栈及其应用。首先会介绍栈的基本结构和基本操作以及代码实现,文后会讲解几个栈的典型应用。栈是一个比较简单但是用途及其广泛的重要的数据结构,所以对于栈的学习重在理解应用而非实现。在今后的学习中可能会遇到各种依赖栈实现的算法或数据结构,一般那种情况下不需要我们自己实现栈,费时费力,一般直接使用C++ STL内置的stack泛型容器,方便快捷。这里讲解栈主要是针对入门的小伙伴~(ps:下面的栈的实现也均使用泛型)
一、栈的定义及实现
首先,阐述一下栈的定义。
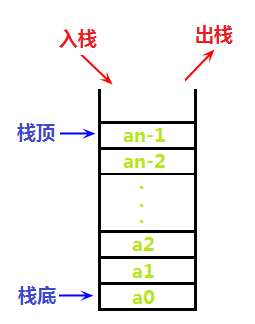
定义:栈是限定仅在表头进行插入和删除操作的线性表。要搞清楚这个概念,首先要明白”栈“原来的意思,如此才能把握本质。"栈“者,存储货物或供旅客住宿的地方,可引申为仓库、中转站,所以引入到计算机领域里,就是指数据暂时存储的地方,所以才有进栈、出栈的说法。
栈也是一种线性表,只不过栈比较特殊,它的运算和操作受限,不同于链表,栈的元素插入和删除仅限于在其一端进行操作。
也就是说,栈这个容器,只能操作当前的首元素,其他元素不可见也不可访问更不可更改。
我们假想栈是一个顶端开口底部封闭的“容器”,我们只能从栈顶“加入物品”,也只能从栈顶“取出物品”,如下图,为了方便展示与理解,我们把线性表“竖着画”:
可见,栈有先进后出或后进先出的特点。
栈的基本运算有以下几种:
(1) 入栈:Push
(2) 出栈:Pop
(3) 取栈顶:Top
(4) 获取大小:Size
(5) 栈是否空:Empty
下面依次介绍这几种运算的原理及实现。
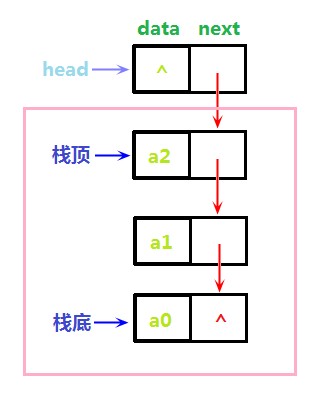
首先需要说的是,栈是一种线性表,所以也会有顺序栈和链式栈,所谓顺序栈,与顺序表类似,就是使用数组来实现栈的相关功能,不过这种方法局限性大,且耗费内存,所以在此不推荐使用,以下所有实现均采用链式结构。
与链表类似,我们首先定义出栈元素结点的结构,同样含有一个值域和一个指针域,如下图所示,粉色框框圈起来的是栈内元素:
结点代码如下:
template
struct Node
{
T data;
Node *next;
}; 接下来我们开始抽象出栈的类结构,我们把栈想象成一条链表,只不过这条链表只能从头部插入元素,只能从头部获取元素,也只能从头部删除元素,这个头部,就是我们栈的栈顶。是不是感觉这其实就是一个操作受限制的链表?而且是逆序建立链表?而且没有需要特殊处理的尾指针?对,就是这样,瞬间就变得简单了。
我们对栈的类定义如下:
template
class Stack
{
private:
Node *head;
int cnt;
public:
Stack()
{
head = new Node;
head->next = NULL;
cnt = 0;
}
void push(T elem); // 将elem元素入栈
void pop(); // 删除栈顶元素
T top(); // 获取栈顶元素值
int size(); // 获取栈内元素数量
bool empty(); // 判断是否为空栈
}; 1. 入栈操作(push)
与链表头部插入一样,首先需要实例化一个新的结点,并给该节点赋初值,使指针p指向该节点,然后通过一下几步:
① 将p指针域指向栈顶结点(首元素),p->next = head->next;
② 将head指针域指向p,head->next=p;
③ 计数器+1
代码如下:
template
void Stack::push(T elem) // 将elem元素入栈
{
Node *p = new Node;
p->data = elem;
p->next = head->next;
head->next = p;
cnt++;
} 2. 出栈操作(pop)
同样,这里的出栈操作其实就是删除栈顶元素,放在单链表里说就是删除首元素,同样是与单链表类似,我们先要获取待删元素的前置结点,也就是head结点(这个好像压根不用获取……),然后使指针p指向head结点的下一结点,执行下列步骤:① 若p为NULL,则说明栈内没有元素,直接返回;否则将head的指针域指向p->next。
② 释放p指向的结点的内存,即delete p;
③ 计数器-1
需要注意的是,如果p为NULL,说明栈空,此时请求pop操作是非法的,可以根据实际情况抛出异常或者返回特殊值,这里方法直接返回。
代码如下:
template
void Stack::pop() // 删除栈顶元素
{
Node *p = head->next;
if(p == NULL)
{
return;
}
head->next = p->next;
delete p;
cnt--;
} 3. 获取栈顶元素(top)
这里直接使用一个p指针指向head->next,如果不为空,则返回p的数据域即可 ;p为NULL的话,说明栈内无元素,此时请求top操作实际上是非法的,可以根据自身情况抛出异常或者返回特殊值。这里采用了返回一个实例化的对象,也就是默认值,代码如下:template
T Stack::top() // 获取栈顶元素值
{
Node *p = head->next;
if(p == NULL) // 如果栈内没有元素,则返回一个新T类型默认值
{
return *(new T);
}
return p->data;
} 4. 获取栈的大小(size)
直接返回内部计数器即可,代码:template
int Stack::size() // 获取栈内元素数量
{
return cnt;
} 5. 判断栈是否为空(empty)
此方法经常在循环操作栈的时候用作条件,如果栈空则返回true,非空返回false。代码如下 :template
bool Stack::empty() // 判断是否为空栈
{
return (cnt == 0);
} **下面是完整的代码以及简短测试用例:
#include
using namespace std;
template
struct Node
{
T data;
Node *next;
};
template
class Stack
{
private:
Node *head;
int cnt;
public:
Stack()
{
head = new Node;
head->next = NULL;
cnt = 0;
}
void push(T elem); // 将elem元素入栈
void pop(); // 删除栈顶元素
T top(); // 获取栈顶元素值
int size(); // 获取栈内元素数量
bool empty(); // 判断是否为空栈
};
template
void Stack::push(T elem) // 将elem元素入栈
{
Node *p = new Node;
p->data = elem;
p->next = head->next;
head->next = p;
cnt++;
}
template
void Stack::pop() // 删除栈顶元素
{
Node *p = head->next;
if(p == NULL)
{
return;
}
head->next = p->next;
delete p;
cnt--;
}
template
T Stack::top() // 获取栈顶元素值
{
Node *p = head->next;
if(p == NULL) // 如果栈内没有元素,则返回一个新T类型默认值
{
return *(new T);
}
return p->data;
}
template
int Stack::size() // 获取栈内元素数量
{
return cnt;
}
template
bool Stack::empty() // 判断是否为空栈
{
return (cnt == 0);
}
int main()
{
Stack st;
st.push(1);
printf("Top: %d, Size: %d\n", st.top(), st.size());
st.push(2);
st.push(666);
printf("Top: %d, Size: %d\n", st.top(), st.size());
st.pop();
printf("Top: %d, Size: %d\n", st.top(), st.size());
st.pop();
st.pop();
printf("Top: %d, Size: %d\n", st.top(), st.size()); // 这里栈空,top()会返回一个随机值
return 0;
} 附个练习,可以用来练习一下栈的基本操作,传送门来了:
SDUT OJ 3335 数据结构实验之栈八:栈的基本操作
二、栈的典型应用
这里是栈的应用,所以需要用到栈的地方我直接使用C++ STL的stack,因为如果我每次都引用我自己写的泛型栈的话,代码太长了……大家可以根据自己的实际情况选择怎么写,编程这个东西,要的就是灵活。
1. 进制转换
进制转换是栈的一个很典型的应用,我们通常说的使用栈解决进制转换问题是指的十进制转换成N进制,因为N进制转十进制根本不需要什么辅助手段,直接一个式子算出来就好……
关于进制转换的数学求法,就不过多赘述了,我记得高中数学好像学过,就是对于十进制整数X,求其N进制表示,使X不断地对N取余数、整除N,如此循环直至X变为0,则所有余数值的逆序序列即为转换后的N进制数。如我们要将十进制数2017转换成八进制,计算过程如图所示:
红色为每步计算的余数,最后余数倒置即为结果。
所以我们的栈就派上了用场,前面介绍栈的特点是“先进后出”或“后进先出”,也就是说,如果一个序列顺序入栈,再全部顺序出栈,则出栈后的序列与出栈前恰好相反,所以恰好可以用来实现序列逆置。
假设这样一个题目:输入两个数X和N,空格间隔,X代表一个十进制正整数,N表示要转换的进制(2<=N<=16),超过10进制的基数用大写ABCDEF表示。求X的N进制表示。
这里我们需要注意的是,超过十进制的基数,也就是说,如果N大于10,那么栈内极有可能有大于等于10的数存在,这时候我们不能原样输出,而是要转换成字母来表示超过9的基础,毕竟数字只有10个,16进制不够用啊QAQ!
我们提前定义好各基数就好,代码如下:
#include
using namespace std;
// 按下标定义余数的输出字符
const char rep[] = "0123456789ABCDEF";
int main()
{
int n,x;
while(~scanf("%d %d", &x, &n))
{
stack st;
while(x)
{
st.push(x % n); // 余数入栈
x /= n; // 整除
}
while(!st.empty())
{
int tp = st.top();
st.pop();
putchar(rep[tp]); // 按照对应的样式输出余数
}
puts("");
}
return 0;
} 这就是栈的一个基本应用——进制转换,实际上就是把一个序列倒序输出,很好地利用了栈的特点。下面给几个练习题传送门:
SDUT OJ 1252 进制转换
SDUT OJ 2131 数据结构实验之栈一:进制转换
2. 行编辑器
我们日常编辑文本文件的时候,一定都会使用退格键,用于删除光标左端的字符,在行编辑器问题上,光标始终在行最右端,不存在移动光标的问题。我们现在引入问题,假设一个简单的行编辑器,用户可以键入字符,也可以敲击退格键删除光标左边的一个字符,也可以敲击删除键来删除整行字符。现在我们把用户键入的按键(注意是按键)转换成一串按键序列,比如abcde#haha##66@qaq代表用户的键入序列,从左至右依次为用户按下的键,“#”代表退格键,删除一个字符;“@”代表删除键,删除整行字符,其它的都代表一个正常的可见字符,现在给定你一串用户的按键序列,让你输出屏幕上最终的字符串(假设输入的字符不包含空格)。
分析这种需求,行编辑器光标始终在右边,输入一个字符就相当于在最右端添加一个字符,删除一个字符也是从最右端删除,删除行则是从右端开始删除所有字符,这正好与栈的运算模式契合,所以使用栈是最好的解决办法。
实现上,从左向右扫描键入序列,如果是“#”,则弹出栈顶元素(需要注意的是,如果栈空,则这个“#”为非法操作,应该直接忽略),“@”则循环弹出栈顶元素直至栈为空,其他情况直接将该字符入栈 。最后将栈内元素依次弹出(此时得到的序列是逆序的,所以需再次逆置,可以再用一个栈辅助逆置),代码如下:
#include
using namespace std;
char line[1010];
int main()
{
while(~scanf("%s", line))
{
stack st;
for(int i = 0 ; line[i] ; i++)
{
if(line[i] == '#')
{
if(!st.empty()) // 非空才删除
st.pop();
}
else if(line[i] == '@')
{
while(!st.empty()) // 循环删除全部元素
st.pop();
}
else
{
st.push(line[i]);
}
}
stack tmp; // 由于出栈结果是倒置的,所以需要使用另一个栈将结果再次倒置
while(!st.empty())
{
tmp.push(st.top());
st.pop();
}
while(!tmp.empty())
{
putchar(tmp.top());
tmp.pop();
}
puts("");
}
return 0;
} 同样,附上练习题传送门:
SDUT OJ 1479 数据结构实验之栈:行编辑器
3. 表达式转换及求值
这里涉及到两点,一点是表达式转换,另一点是表达式求值,下面分别介绍
(1) 表达式转换
我们日常算术中使用的表达式是中缀式,通常是符号位于操作数中间,这种表达方式需要考虑算符的优先级问题,所以引入括号来强行更改算术优先级。这种中缀式适合人脑计算,比较符合人类的运算习惯,但是对计算机却很不友好,解析难度较大,所以引入了前缀式和后缀式,这两种表达式均没有括号,且无优先级限制,只需要按照书写顺序进行计算即可,不同于中缀式,后缀式只需要使用一个栈进行相关操作即可,而中缀式需要两个栈,一个存符号,一个存操作数。
下面分析一个表达式转换问题。
我们要做的是将一个中缀表达式转换成后缀表达式(前缀我们暂不考虑,与后缀大同小异),中缀表达式里包含+-*/和括号。
下面给出转换方法:
① 首先构造一个符号栈,此栈的特点是要求遵循栈内元素自底向上优先级严格递增原则,也就是说,上面的元素优先级必须大于下面的元素优先级(前缀式是大于等于,这点区别一定要记清楚)。
② 从左向右扫描表达式(前缀式从右向左),逐步判断:
a) 如果遇到运算数,则直接输出
b) 如果是运算符,则比较优先级,如果当前运算符优先级大于栈顶运算符优先级(栈空或栈顶为括号时,直接入栈 ),则将运算符入栈;否则弹出并输出栈顶运算符,直至满足当前运算符大于栈顶运算符优先级(或者栈变空、栈顶为括号)为止,然后再将当前运算符入栈。
c) 如果是括号,则特殊处理。左括号的话,直接入栈;右括号的话,则不断弹出并输出栈顶符号,直到栈顶符号是左括号,然后弹出栈顶左括号(不输出,因为后缀式没有括号),并忽略当前右括号,继续扫描。
d) 由以上步骤可知,括号具有特殊的优先级,左括号在栈外的时候,是最高的优先级,在栈内有最低优先级。
③ 重复上述步骤,直到表达式扫描结束,此时若栈内有剩余符号,则将符号依次出栈并输出。
例如:将a*b+(c-d/e)*f转换成后缀表达式,分解步骤如下:
上表即为表达式转换的分解步骤,利用了栈的特性完成转换,转换后的后缀表达式不需要考虑算符优先级,只要按照符号出现的顺序进行计算即可,下一小节就会讲利用栈求后缀式的计算结果值。
中缀式转后缀式代码如下(简化版,假设运算数是小写字母,运算符只有四则运算和括号):
#include
using namespace std;
char line[1010]; // 输入的中缀式
char res[1010]; // 保存结果
int level[128]; // 定义运算符的优先级
// 比较两运算符优先级,如果a>b返回true,否则false
bool operatorCmp(char a, char b)
{
return level[(int)a] > level[(int)b];
}
int main()
{
// 初始化定义运算符优先级
level['+'] = level['-'] = 1;
level['*'] = level['/'] = 2;
while(~scanf("%s", line))
{
stack st;
int ptr = 0; // 初始化结果字符串指针
for(int i = 0 ; line[i] ; i++)
{
if(isalpha(line[i])) // 如果是字母
{
res[ptr++] = line[i]; // 暂存到结果字符数组
}
else // 否则,运算符或括号
{
// 可以直接入栈的情况:栈空、栈顶括号、当前是括号
// 认真思考一下这个短路条件的内涵
if(st.empty() || st.top() == '(' || line[i] == '(')
{
st.push(line[i]);
}
else if(line[i] == ')') // 右括号,弹出栈内符号直至遇到左括号
{
// 这里也有一个短路条件,如果弹出过程遇到栈空,说明括号不匹配,应该报错
while(!st.empty() && st.top() != '(')
{
res[ptr++] = st.top();
st.pop();
}
// 弹出左括号
if(!st.empty())
st.pop();
}
else
{
// 遇到符号,如果栈非空且当前符号小于等于栈顶符号,则一直弹出并输出栈顶符号
while(!st.empty() && !operatorCmp(line[i], st.top()))
{
res[ptr++] = st.top();
st.pop();
}
// 循环结束,可以入栈了
st.push(line[i]);
}
}
}
// 扫描结束,依次弹出并输出栈内剩余元素
while(!st.empty())
{
res[ptr++] = st.top();
st.pop();
}
// 为结果字符串添加结束标志'\0'
res[ptr] = 0;
// 打印转换结果
puts(res);
}
return 0;
} 同样附上练习题,传送门:
SDUT OJ 2132 数据结构实验之栈二:一般算术表达式转换成后缀式(此题与上面例子很像,但是有细节差异哦)
SDUT OJ 2484 算术表达式的转换(此题要求前缀,与后缀类似,相信你可以触类旁通~)
(2) 后缀表达式计算
前面说到,后缀式很适合计算机识别,所以后缀式求值只需要利用一个栈即可快速求值。而且实现起来也很简单。
由于后缀式不存在优先级,所以计算起来也没那么麻烦,下面给出计算步骤。
步骤如下:
① 构造一个操作数栈,用于存放操作数。
② 从左向右扫描后缀式,如果遇到操作数,则将操作数入栈;
③ 如果遇到运算符,根据运算符需要的运算数的个数,从栈中取出对应个数的操作数,先出栈的作为右操作数,后出栈的为左操作数,计算出结果后,将计算结果入栈。
④ 扫描结束后,如果后缀式合法,则过程中不会产生错误且最终栈内一定有且仅有一个元素,输出栈顶元素即为最终结果。
我们以后缀式59*684/-3*+为例,这里的操作数均为个位数(前面不是59而是5和9),当然有更复杂的后缀式,比如多位数,这里不研究。
解析如下:
利用一个数栈,即可完成后缀表达式的计算,且不用考虑优先级,需要注意的是不遵循交换律的运算(-和/)要注意左右操作数,先出栈的为右操作数!
上例后缀式求值代码如下:
#include
using namespace std;
char line[1010];
int calc(int a, int b, char op)
{
if(op == '+')
return a + b;
else if(op == '-')
return a - b;
else if(op == '*')
return a * b;
else // '/'
return a / b;
}
int main()
{
while(~scanf("%s", line))
{
stack st; // 构造操作数栈
for(int i = 0 ; line[i] ; i++)
{
if(isdigit(line[i])) // 如果是数字(操作数),入栈
{
st.push(line[i] - '0');
}
else // 如果是符号
{
int b = st.top(); // 取出第一个运算数,也就是右操作数
st.pop();
int a = st.top(); // 取出第二个运算数,也就是左操作数
st.pop();
st.push(calc(a, b, line[i])); // 计算结果并入栈
}
}
printf("%d\n", st.top()); // 输出结果
}
return 0;
} 附练习题传送门:
SDUT OJ 2133 数据结构实验之栈三:后缀式求值
4. 括号匹配
下面就是本章栈的另一个重要的应用了——括号匹配,这也是一个比较常见的应用。简单点说,就是给你一串括号序列,让你判断此序列是否是合法的括号匹配序列。比如,(())就是一个合法序列,而)()(就不是合法序列,同样(][)也不是合法序列,诸如此类……
接下来,我们引入一个问题,给定一串带各种括号的表达式序列或括号序列,可能包括括号、数字、字母、标点符号、空格,括号包括圆括号(),方括号[],花括号{},让你判断给定序列是不是括号匹配的,匹配输出yes,否则输出no。
例如,sin(20+10)是匹配的,{[}]是不匹配的。
我们先分析算法:
首先,判断一对括号匹配,一定是右括号匹配最近的左括号。也就是说,每遇到一个右括号,左边都会有一个唯一的左括号与之匹配,当所有右括号与所有左括号匹配完成,没有多余的左括号,则匹配成功,否则失败。
所以我们可以利用一个栈来存储括号:我们从左向右扫描序列,遇到左括号,就直接入栈;遇到右括号,我们就检查栈顶是不是与之对应的左括号,如果是,则匹配,弹出栈顶元素,继续扫描;否则,说明该右括号无匹配的左括号,则失败,该序列不匹配。
实现起来还是很容易的,直接上代码了:
#include
using namespace std;
// 给定左符号a和右符号b判断是否匹配
bool match(char a, char b)
{
if( (a == '(' && b == ')') ||
(a == '[' && b == ']') ||
(a == '{' && b == '}'))
return true;
return false;
}
// 判断给定字符串是否是括号匹配的
bool check(char *s)
{
stack st;
for(int i = 0 ; s[i] ; i++)
{
if(s[i] == '(' || s[i] == '[' || s[i] == '{')
{
// 左括号直接入栈
st.push(s[i]);
}
else if(s[i] == ')' || s[i] == ']' || s[i] == '}')
{
// 如果遇到右括号时,栈空,或者栈顶元素与这个右括号不匹配,直接false
if(st.empty() || !match(st.top(), s[i]))
return false;
// 执行到这里说明上一步匹配成功,弹出栈顶左括号
st.pop();
}
// else 扫描到其他情况,非括号直接不考虑
}
// 扫描结束后,只有栈为空才是括号匹配的,否则说明栈内有左括号未被匹配
return st.empty();
}
int main()
{
char str[110];
while(gets(str))
{
// 检查是否匹配
puts(check(str) ? "yes" : "no");
}
return 0;
} SDUT OJ 2134 数据结构实验之栈四:括号匹配 (此题与上例一样)
5. 出栈序列的判定
我们通过先前的学习知道,栈是先进后出结构,正是这种特性决定了栈在计算机领域的重要地位。现在有这样一个问题:有一个待入栈序列,你需要将个序列中的元素依次入栈,你可以随时将某元素出栈,这样可以得到一个出栈序列。例如有入栈序列1,2,3,4,5,依次执行push,push,push,pop,pop,pop,push,pop,push,pop,可得到出栈序列3,2,1,4,5。
现在给定你一个待入栈的序列,再给定若干个待判定序列,你需要判断这些待判定序列是否是待入栈序列的合法出栈序列。
例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该入栈序列对应的一个出栈序列,但4,3,5,1,2就不可能是该序列的出栈序列。假设压入栈的所有数字均不相等。
提出问题,假设第一行输入n,代表序列长度,随后一行n个整数,代表序列,第三行输入m,代表待匹配出栈序列的个数,接下来m行,每行n个数代表出栈序列。
其实此题可以根据栈的特性设计算法来快速解决,但是我们这里不考虑,我们只用栈模拟解决 。我们假设给定出栈序列合法,设置一个指针指向出栈序列首端,表示待匹配元素,那么我们将待入栈序列依次入栈,每入栈一个元素,判断一下当前栈顶是不是与指针指向的出栈序列元素匹配,匹配的话,说明该栈顶元素需要出栈,然后还需将指针后移,然后继续判断栈顶和指针元素是否匹配,如此循环直至不匹配;否则继续将待入栈序列入栈。当待入栈序列全部入栈完毕,检查此时栈是否为空。若栈为空,说明入栈序列与出栈序列全部匹配,该出栈序列合法,否则说明不匹配,出栈序列不合法。代码如下:
#include
using namespace std;
int arr[10010];
int chk[10010];
int main()
{
int n, m;
while(~scanf("%d", &n))
{
for(int i = 0 ; i < n ; i++)
scanf("%d", &arr[i]);
scanf("%d", &m);
while(m--)
{
for(int i = 0 ; i < n ; i++)
scanf("%d", &chk[i]);
stack st;
int ptr = 0; // 初始化出栈序列匹配元素的指针
for(int i = 0 ; i < n ; i++)
{
// 将入栈序列的元素依次入栈
st.push(arr[i]);
while(!st.empty() && st.top() == chk[ptr])
{
// 如果栈不空且栈顶与指针所指匹配,就弹出栈顶并移动指针
st.pop();
ptr++;
}
// 不匹配了,就继续入栈序列元素
}
if(st.empty()) // 栈空,说明所有元素匹配,序列合法
puts("yes");
else // 否则,说明存在未匹配元素,序列不合法
puts("no");
}
}
return 0;
}
附练习题传送门,其实就是这个题……
SDUT OJ 3334 数据结构实验之栈七:出栈序列判定
6. 迷宫问题
迷宫问题的求解,我们通常使用两种最经典的搜索方式——深度优先搜索(Depth First Search, DFS)或广度优先搜索(Breadth First Search, BFS)。我们本章是栈,所以暂且不讲这两种搜索,后面二叉树的章节会学到这两种搜索方式。先透露一下,深度优先搜索,是函数递归式的,是利用了函数栈的特性;广度优先搜索的实现 ,需要依赖队列来维护一个搜索序列。所以栈和队列这两种数据结构的重要性不言而喻。
迷宫求解问题,我们假设有如下问题:
一个由n * m 个格子组成的迷宫,起点是(1, 1), 终点是(n, m),每次可以向上下左右四个方向任意走一步,并且有些格子是不能走动,求从起点到终点经过每个格子至多一次的走法数(也就是路线的种数)。
我们回归到问题,假设啊,我们用人类的思维方式走迷宫,我不知道你们是怎么做的,反正我是遵循“不撞南墙不回头”的策略,按照一条路走下去,碰壁了再原路返回,这样逐步地尝试,就会找到出口。我们的深度优先搜索就是“撞南墙”式的搜索方式,按照一个方向不断地找下去,直至无法继续,再改变方向继续寻找,再直至所有方向都尝试完,搜索结束。
那么用栈如何解决呢?其实函数递归就是栈的典型应用,我们知道,递归其实就是把函数的各参数和入口地址等信息保存到函数栈中,执行的始终是栈顶函数,结束后弹出函数栈执行上一层函数……如此下去,所以这里深搜的递归问题完全可以用栈来解决,我们先图解一个4*4迷宫,假设我们定义方向的优先顺序为右下左上顺时针,即RDLU,如下图(图很大,我可以自己用Windows画图画了好久,绿色起点,粉色终点,看不清请点大图):
根据上图可以看出,我们在“撞南墙”后需要回退到上一步的操作,这就涉及到保存先前走迷宫的状态,包括走过的格子和每个格子当时所朝向的方向,所以恰好可以用栈来保存状态,因为每次回退的时候,其实就是弹出栈顶元素,这样栈顶元素始终是最后一次操作的状态。
我们使用一个三元组(x,y,d)来保存迷宫路径状态,x和y分别代表迷宫格子的行列位置,d代表这个格子当前所朝向的方向。注意我们的方向只有四个,且每个方向最多枚举一次(方向不能无限地来回转啊,这样永远没完没了了)。比如我们将上面的迷宫图按照步骤画出栈内状态(又要祭出我的大Windows画图了,假设左上角是1,1):
这样按照步骤一步一步来,是不是就清晰明了了?下面给出代码,代码中有注释帮助你们自己分析思考,dfs_recursive是递归形式的解法,比较简单,你们可以自己实现一下~上代码:
#include
using namespace std;
template
struct tuple // 自定义一个泛型三元组
{
T1 first;
T2 second;
T3 third;
tuple(T1 a, T2 b, T3 c):first(a), second(b), third(c){} // 三元组的构造
};
typedef tuple tpl; // 重定义以下写起来方便……
const int dx[] = {0,1,0,-1}; // 行上的方向
const int dy[] = {1,0,-1,0}; // 列上的方向
// dx dy取相同下标时可表示为一个方向,例如dx[0]和dy[0]表示的是右
int mp[10][10]; // 地图数据
bool vis[10][10]; // 标记数组
int dfs_stack(int n, int m) // 非递归(栈实现)的深度搜索
{
int res = 0;
memset(vis, 0, sizeof(vis)); // 多组数据一定记得初始化这些有标记意义的数组或对象
stack st;
st.push(tpl(1, 1, -1)); // 将起点入栈这里初始方向写成-1
// 是因为每次取出栈顶均要通过+1来更改方向,
// 所以初始-1的话,+1才会变成0
vis[1][1] = true; // 标记此点已在栈中,代表该点是当前已走路径上的点
while(!st.empty())
{
/**
* 此题求路径数,所以就算找到终点也要回退
* 继续找其他可能的路径,所以条件是栈空
* (说明已经退到底了)才结束
**/
tpl tmp = st.top(); // 取栈顶元素开始枚举下一步能达到的点
st.pop(); // 这里先弹出,因为要更改方向,方向更改完成后还要放回栈中,除非无路可走要退回
int x = tmp.first;
int y = tmp.second;
vis[x][y] = false; // 同样先取消标记,因为已经出栈了
if(x == n && y == m)
{
res++; // 当前点是终点,计数器加1,表示已经搜寻到一条路径
continue;
}
int d;
for(d = tmp.third + 1 ; d < 4 ; d++) // 顺时针更改方向
{
// 根据方向得到下一步尝试(划重点,尝试)到达的点
int px = tmp.first + dx[d];
int py = tmp.second + dy[d];
if(px > 0 && px <= n && py > 0 && py <= m && !vis[px][py] && mp[px][py] == 0)
{
// 如果该尝试的点未出界且未在栈内且不是障碍物,则可通行
tmp.third = d; // 更改栈顶元素的方向值
st.push(tmp); // 放回栈内
vis[x][y] = true; // 做上标记,表示在栈中
st.push(tpl(px, py, -1)); // 把可通行的点入栈,方向初始化为-1
vis[px][py] = true; // 做上入栈标记
break; // 跳出循环,一定要跳出,因为已经找到下一步路了,不要再枚举方向了
}
}
// 如果循环可以正常结束(非break),那么说明当前栈顶点已经枚举完所有的方向了,可以回退
// 在这里回退表现的是没经过修改方向后再次入栈这一步,因为没走break,仔细看
}
return res;
}
int dfs_recursive(int n, int m) // 递归的深度搜索(自己实现)
{
return 0;
}
int main()
{
int t,n,m;
while(~scanf("%d", &t))
{
while(t--)
{
scanf("%d %d", &n, &m);
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= m ; j++)
scanf("%d", &mp[i][j]);
printf("%d\n", dfs_stack(n, m));
}
}
return 0;
} SDUT OJ 2449 走迷宫
以上就是本章全部内容了,栈还是一个比较简单的数据结构,但是对于计算机的意义是相当重大的。我们日常使用的操作系统都离不开栈,线程栈、任务栈、进程栈、各种栈……包括我们编程接触的函数递归在运行时也里不开栈,总之,学习并深刻理解栈是相当重要的。如果文中有描述不当或者讲解错误的地方,欢迎大家留言指正~
下集预告&传送门:数据结构与算法专题之线性表——队列及其应用