数据结构与算法专题之线性表——队列及其应用
本章内容是数据结构与算法第三弹——队列及其应用。与前一章栈的讲解一样,本章对于队列的讲解也会首先介绍栈的基本概念及结构和代码实现,然后再引入几个经典的队列问题帮助大家理解队列的应用。
队列与栈一样,也是一个简单但相当重要的数据结构,重点也应该落在对于队列的理解应用而非代码实现上,在今后的数据结构与算法的学习中也会学到多种依赖于队列的算法,同样我们在那时候会使用C++ STL的queue泛型容器,本文前半部分介绍的队列也将使用泛型,实现STL queue里的大部分方法。
队列的概念与实现
我们先来认识一下队列。
队列,顾名思义,是一个“排队的序列”,它与栈一样,是一个操作受限的线性表,只不过栈的插入删除都限制在同一端(也就是栈顶),而队列的插入和删除分别限制在两端。也就是说,队列只能从一端插入数据,从另一端删除数据,就像餐厅排队一样,新来的人只能排在队伍最后面,队伍里最前面打完饭的人离开。我们把队列插入数据的一端称为队尾,删除数据的一端称谓队首,想想排队,是一个原理。
我们假设一个队列左边是队首,右边是队尾,一个基本的队列示意图如下:
可见,插入数据总是在队尾操作,删除数据总是在队首操作,当然,我们只能访问到队首元素,所以,队列是一个先进先出(FIFO)结构。
我们为队列定义下面几个方法:
(1) 入队:Push
(2) 出队:Pop
(3) 取队首:Front
(4) 获取大小:Size
(5) 队列是否空:Empty
看这些方法,是不是跟栈很像呢?下面我们会依次来介绍并实现这些方法。
由于队列也是线性表,所以与栈、链表一样,也有顺序结构和链式结构,在前一章关于栈的顺序结构已经说了,它是比较耗费内存的,但是队列与栈又有所不同,我们这里简单介绍一下顺序结构,主要内容还是讲链式结构。
队列的顺序结构
顺序结构概述
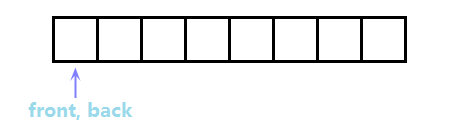
所谓顺序结构,其实就是一个大小固定的数组,拥有队首指针front和队尾指针back,初始队列为空时,front与back相等且都为0,如图:
容易看出,我们的数组构造成多大,队列的极限容量就是多大,上图中,队列最大容量为8,这也是顺序结构的局限性,无法动态扩展空间。
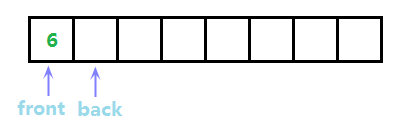
当我们插入元素时,实际上就是把元素赋值到back指针所指的地方,然后back后移,假设我们插入了整数6,如下图:
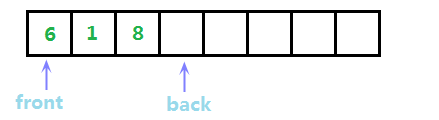
可以看出,现在我们队首元素就是front指针所指位置,队列元素数量(size)是back-front=1,我们假设依次插入了1和8,此时队列变成下图:
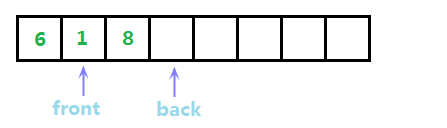
此时,我们执行pop,删除队首元素,事实上我们不需要真正的删除front所指的那个6,只需要将front指针后移一位即可,这样我们获取到的队首元素就变成front所指的元素1了,如图:
此时队列大小为back-front=2。聪明的你或许已经看出问题了,不管是删除还是添加,两个指针永远都只会向后移,这样总会超出数组的范围,出现“上溢出”现象(也叫假溢出,由于存储区未满但指针超出界限发生溢出,故称为假溢出),而且执行删除操作以后,front指针之前的元素位置就会浪费掉,再也不会被访问。没错,这样的队列实用性极低,所以对于顺序结构的队列,我们需要将其改造成循环队列。
循环队列概述
那么何为循环队列?循环队列就是当其中一个指针超出数组时,返回数组的首元素,参照循环链表,也就是将数组首尾相连变成一个圈儿,这样指针就能在数组范围内循环起来,不至于发生溢出,如图所示,我们将上图直的数组“掰弯”,使其变成循环的(粉色数字是原数组下标):
这样的话,指针就不会溢出了。当然,我们不可能把顺序表从内存中的逻辑顺序变成环状,但是我们观察下标值,可以发现,我们要的是指针在下标7时,移动一下会变成下标0,想到了没?对,就是模运算。我们已知数组大小是8,所以怎样使7+1=0?答案就是(7+1)%8=0,溢出归零。
所以在不改变顺序表结构的前提下,只需要把指针移动的操作由back+1改为(back+1)%size即可(size为数组总长度,front同理)。变成循环队列以后,求队列元素个数就不能简单地使用back-front了,而应该使用(back-front+size)%size,为什么要+size呢?因为back-front可能出现负数,所以我们要加上模,然后再取模,就可以得到答案了,可以自己简单地举几个例子试验一下。
接下来我们分析一下这front和back两个指针,回到上图的圈圈里,添加元素实际上是back指针顺时针移动,删除元素事实上是front指针顺时针移动,也就是说,添加和删除是两个指针“互相追赶”的过程。如果back追赶front,说明是插入元素,追上了的话,说明队列满;如果front追赶back,说明是删除元素,追上了就说明队列空。
由于指针始终是顺时针方向移动,而back指针总是比front指针超前(也就是说front指针无论怎么追赶,只会赶上back而不会超过back,因为添加的元素始终要比删除的元素多),所以由front指针开始,按照顺时针方向到back指针所经过的所有元素,就是队列中的元素(思考一下为什么)。
但是这里出来了一个特殊情况,如果back指针和front指针重合了,那么算是队列空,还是算队列满呢?
这里就不太好确定了,因为你不清楚是back追上了front还是front追上了back,所以我们要避开这种特殊情况,怎么办呢?就是始终在back后面留一个空位置,使back永远不会追上front,但front依然可以追上back,这样当两指针重合时,就可以确定是front追上back导致的重合,也就是删除导致的,也就是队空的情况。
所以对于队空和队满的判定:
☆队列空:指针front==back时
★队列满:当(back+1)%size==front时(+1的原因是因为预留空位了)
顺序队列的实现
这里直接给出顺序循环队列的实现代码,留作大家自己思考:
#include
using namespace std;
template
class CQueue
{
private:
T* arr; // 顺序表
int _front, _back; // 两指针
int sz; // 队列最大容量
public:
CQueue(int sz) // 构造一个顺序队列,声明其最大容量
{
arr = new T[sz + 1]; // 因为要back指针预留一个元素的位置
this->sz = sz;
_front = _back = 0;
}
void push(T elem); // 入队操作
void pop(); // 出队操作
T front(); // 获取队首元素
int size(); // 获取队内元素数量
bool empty(); // 判断队空
};
template
void CQueue::push(T elem) // 入队操作
{
if((_back + 1) % sz == _front) // 队列满,忽略
return;
arr[_back] = elem;
_back = (_back + 1) % sz;
}
template
void CQueue::pop() // 出队操作
{
if(_front == _back) // 队空,忽略
return;
_front = (_front + 1) % sz;
}
template
T CQueue::front() // 获取队首元素
{
if(_front == _back) // 队空,返回默认值
return *new T;
return arr[_front];
}
template
int CQueue::size() // 获取队内元素数量
{
return (_back - _front + sz ) % sz;
}
template
bool CQueue::empty() // 判断队空
{
return _front == _back;
}
int main()
{
CQueue q(10);
q.push(1);
printf("%d\n", q.front());
q.push(2);
q.push(3);
printf("%d\n", q.front());
q.pop();
printf("%d\n", q.front());
q.pop();
printf("%d\n", q.front());
return 0;
}
队列的链式结构
基本结构定义
上面讲了队列的顺序结构,实现起来比较简单,就是理解起来稍微有那么一点点困难。可以看出顺序结构的局限性还是相当大的,所以我们在不确定队列最大值的情况下,一般使用链式结构,可以动态地管理空间,既不会出现空间不足,也不会出现空间浪费的情况。同链式栈一样,链式队列也是一个单链表,结构上与单链表一模一样,我们来看一下单链表变成链式栈和链式队列的区别:
链式栈:无需尾指针,插入、删除和查询均在head结点后操作。
链式队列:需要尾指针,插入在tail指针上操作,查询和删除在head结点后操作。
所以一个基本的链式队列如下图:
(其实这个图就是我把单链表的图拿来改了改……)可以看到,结构与单链表一致,push操作相当于单链表的push_back,而pop和front都是操作第一个元素,实现起来也很简单,所以,结点的结构代码:
template
struct Node
{
T data;
Node *next;
}; template
class Queue
{
private:
Node *head, *tail;
int cnt;
public:
Queue()
{
head = new Node;
head->next = NULL;
tail = head;
cnt = 0;
}
void push(T elem); // 将elem元素入队
void pop(); // 弹出队首元素
T front(); // 获取队首元素值
int size(); // 获取队内元素数量
bool empty(); // 判断是否为空队列
}; 1. 入队操作(push)
入队操作,由于新元素的添加是在队尾进行的,所以相当于单链表的push_back操作,所以步骤如下:
① 构造一个新结点p并赋值,并且将p的指针域置为NULL
② 将tail的指针域置为p
③ 修改tail的指向为新节点p
代码如下:
template
void Queue::push(T elem) // 将elem元素入队
{
// 此操作与单链表push_back一致
Node *p = new Node;
p->data = elem;
p->next = tail->next;
tail->next = p;
tail = p;
cnt++;
}
2. 出队操作(pop)
这里的出队操作与栈的出栈操作是一致的,都是在链表头部进行的,我们首先要获取首元素,也就是head->next,赋值给指针p
① 若p为NULL,则说明队列内没有元素,直接返回;否则将head的指针域指向p->next。
② 释放p指向的结点的内存,即delete p;
③ 计数器-1
同样需要注意的是,如果p为NULL,说明队列空,此时请求pop操作是非法的,可以根据实际情况抛出异常或者返回特殊值,这里方法直接返回。
还有一点与栈不同,由于队列含有尾指针,所以当队列内只有一个元素时,删除该元素的同时也需要将tail尾指针重置,即tail=head。
实现代码如下:
template
void Queue::pop() // 弹出队首元素
{
Node *p = head->next;
if(p == NULL)
return;
head->next = p->next;
delete p;
if(cnt == 1) // 只有一个元素,移动尾指针
tail = head;
cnt--;
} 3. 获取队首元素(front)
同样地,直接返回head->next指向的元素的值,若指向为空,则抛出异常或返回特殊值。
代码如下:
template
T Queue::front() // 获取队首元素值
{
Node *p = head->next;
if(p == NULL) // 如果队内没有元素,则返回一个新T类型默认值
return *(new T);
return p->data;
} 4. 获取队列元素个数(size)
直接返回内部计数器,代码:
template
int Queue::size() // 获取队内元素数量
{
return cnt;
} 5. 判断队列是否为空(empty)
若队空,返回true,否则返回false,代码:
template
bool Queue::empty() // 判断是否为空队列
{
return (cnt == 0);
} **下面是完整的队列类代码
#include
using namespace std;
template
struct Node
{
T data;
Node *next;
};
template
class Queue
{
private:
Node *head, *tail;
int cnt;
public:
Queue()
{
head = new Node;
head->next = NULL;
tail = head;
cnt = 0;
}
void push(T elem); // 将elem元素入队
void pop(); // 弹出队首元素
T front(); // 获取队首元素值
int size(); // 获取队内元素数量
bool empty(); // 判断是否为空队列
};
template
void Queue::push(T elem) // 将elem元素入队
{
// 此操作与单链表push_back一致
Node *p = new Node;
p->data = elem;
p->next = tail->next;
tail->next = p;
tail = p;
cnt++;
}
template
void Queue::pop() // 弹出队首元素
{
Node *p = head->next;
if(p == NULL)
return;
head->next = p->next;
delete p;
if(cnt == 1) // 只有一个元素,移动尾指针
tail = head;
cnt--;
}
template
T Queue::front() // 获取队首元素值
{
Node *p = head->next;
if(p == NULL) // 如果队内没有元素,则返回一个新T类型默认值
return *(new T);
return p->data;
}
template
int Queue::size() // 获取队内元素数量
{
return cnt;
}
template
bool Queue::empty() // 判断是否为空队列
{
return (cnt == 0);
}
int main()
{
return 0;
}
以上就是队列的实现及概念的全部内容,附个练习题的传送门:
SDUT OJ 2135 数据结构实验之队列一:排队买饭下集预告&传送门:数据结构与算法专题之串——字符串及KMP算法