二叉树——堆

二叉树顺序存储结构

  理解堆之前先理解一下二叉树的顺序存储结构。普通的二叉树并不适合顺序存储，因为可能会造成大量的空间浪费。只有完全二叉树适合顺序结构存储。显示中我们通常把堆使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统中虚拟进程地中空间中的堆是两回事，这个堆是一个数据结构，而虚拟进程地址空间中的堆是操作系统中管理内存的一块区域分段。

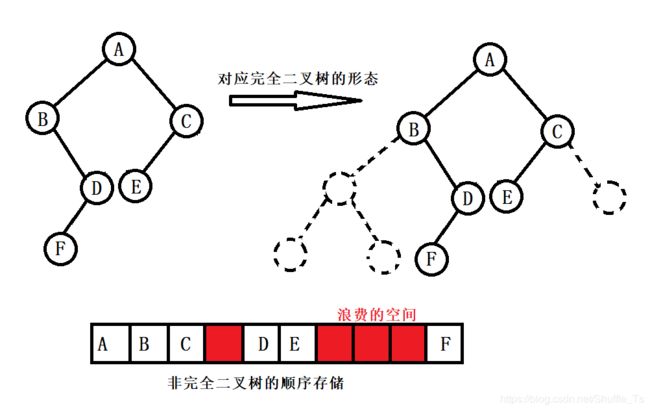
堆的概念

  如果有一个关键码集合K={k0，k1，……kn-1}，把所有的元素按完全二叉树的吮吸存储方式存储在一个一维数组，并满足：ki<=k2i+1并且ki<=k2i+2，就程这个二叉树为小堆（大堆）。根节点是最大值的堆称为大堆，根节点为最小值称为小堆。

堆的性质

1. 队中每个结点的值总是不大于或者不小于其父节点
2. 堆总是一个完全二叉树
3. 堆中第N个节点的左孩子为第N2+1个节点，右孩子为第N2+2个节点
   

堆的实现

创建堆

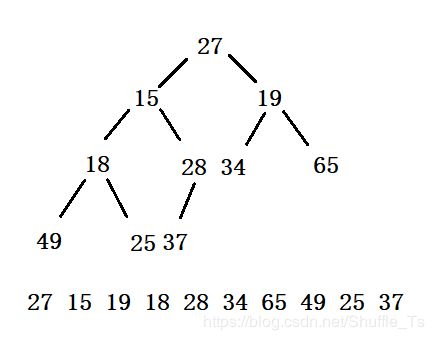
  这个数组从逻辑上可以看作是一个完全二叉树，但他还不是一个堆，需要我们运用向下调整算法将他构成一个堆。对于二叉树来说，如果根节点的左右子树都满足堆，那么这个二叉树就满足堆，所以我们从倒数第二个尾叶子节点开始调整，一直调整到到整个二叉树的根节点为止。

向下调整算法（小堆）

  向下调整算法就是从当前节点开始，依次向下调整，直到不满足条件为止：

1. 找出当前节点的两个孩子中的最小的孩子（先找左孩子，根据完全二叉树的性质可以直到左孩子存在，右孩子不一定存在）
2. 如果当前节点比最小的孩子大，就需要与这个孩子交换位置，然后继续向下调整
3. 如果当前节点比最小的孩子小，就可以结束调整，说明以当前节点为根的二叉树是小堆。
   
   向下调整代码

void AdjustDown(HPData* array, int size, int root, PCOM compare)
{
	int child = root * 2 + 1;
	while (child < size)
	{
		//找左右孩子中最小的孩子
		if (child + 1 < size && compare(array[child],array[child - 1]))
			child += 1;

		if (compare(array[child], array[root]))
		{
			swap(array[root], array[child]);
			root = child;
			child = root * 2 + 1;
		}
		else
			return;
	}
}

堆插入

  堆创建好了，接下来就是向堆中插元素，只需要将元素放在堆底，然后向上调整
  向上调整就是用当前节点与父节点比较，如果比父结点小，就要交换，然后继续向上调整，如果比父结点大，就结束调整

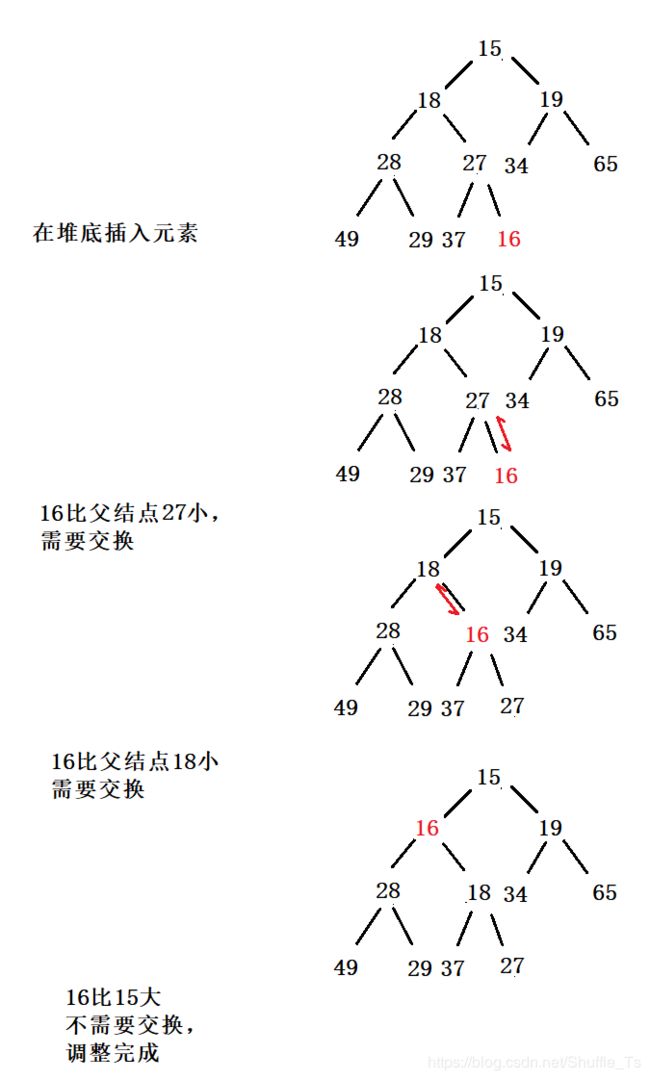
堆删除

  堆删除时将对顶元素删除，先将堆顶元素和最后一个元素交换位置，将最后一个元素删除即可，最后从堆顶向下调整。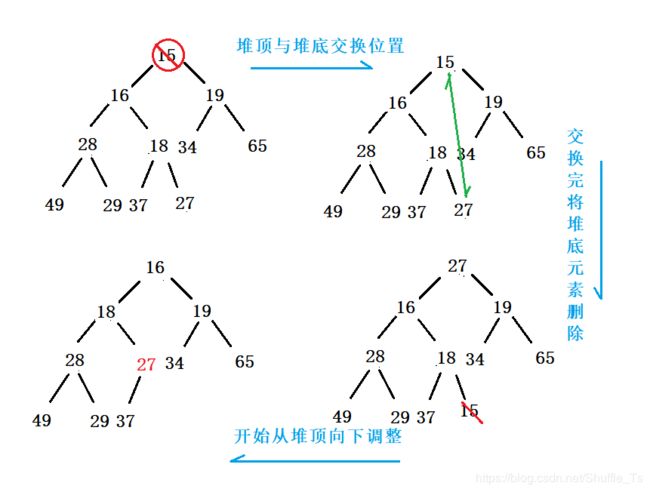

堆代码的实现

int less(HPData left, HPData right)
{
	return left < right;
}
int greater(HPData left, HPData right)
{
	return left > right;
}
//定义函数指针来改变大堆和小堆
typedef int(*PCOM)(HPData left, HPData right);
int less(HPData left, HPData right);
int greater(HPData left, HPData right);

//堆结构体
typedef struct Heap
{
	HPData* _array;
	int _size;
	int _capacity;
	PCOM _compare;
}Heap;

//向下调整
void AdjustDown(HPData* array, int size, int root, PCOM compare)
{
	int child = root * 2 + 1;
	while (child < size)
	{
		//找左右孩子中最小的孩子
		if (child + 1 < size && compare(array[child],array[child - 1]))
			child += 1;

		
		if (compare(array[child], array[root]))
		{
			swap(array[root], array[child]);
			root = child;
			child = root * 2 + 1;
		}
		else
			return;
	}
}

//向上调整
void AdjustUp(HPData* array, int size, int child, PCOM compare)
{
	int root = (child - 1) >> 1;

	while (child)
	{
		if (compare(array[child], array[root]))
		{
			swap(array[root], array[child]);
			child = root;
			root = (child - 1) >> 1;
		}
		else
			return;
	}
}

//堆扩容
void CheckCapacity(Heap* hp)
{
	assert(hp);
	int newcapacity = hp->_size * 2;
	HPData* array = (HPData*)malloc(sizeof(HPData) * newcapacity);
	if (array == NULL)
	{
		assert(0);
		return;
	}

	for (int i = 0; i < hp->_size; ++i)
		array[i] = hp->_array[i];
	hp->_capacity = newcapacity;

	free(hp->_array);
	hp->_array = array;
}

//初始化堆
void InitHeap(Heap* hp, HPData* array, int size, PCOM compare)
{
	assert(hp);
	hp->_array = (HPData*)malloc(sizeof(HPData)*size);
	if (NULL == hp->_array)
	{
		assert(0);
		return;
	}

	hp->_capacity = size;
	hp->_size = size;
	hp->_compare = compare;
	for (int i = 0; i < size; ++i)
		hp->_array[i] = array[i];

	int root = ((size - 2) >> 1);
	for ( ;root >= 0; --root)
		AdjustDown(hp->_array, size, root, compare);
}

//堆插入
void InsertHeap(Heap* hp, HPData data, PCOM compare)
{
	if (hp->_size == hp->_capacity)
		CheckCapacity(hp);
	hp->_array[hp->_size] = data;
	AdjustUp(hp->_array, hp->_size, hp->_size - 1, compare);

}

//堆中元素个数
int HeapSize(Heap* hp)
{
	assert(hp);
	return hp->_size;
}

//堆顶元素
HPData HeapTop(Heap* hp)
{
	assert(hp);
	return hp->_array[0];
}

//判断是否是空堆
bool HeapEmpty(Heap* hp)
{
	assert(hp);
	return hp->_size == 0;
}

//删除堆元素
void EraseHeap(Heap* hp)
{
	if (HeapEmpty(hp))
		return;
	swap(hp->_array[0], hp->_array[hp->_size - 1]);
	hp->_size -= 1;
	AdjustDown(hp->_array, hp->_size, 0, hp->_compare);
}

//销毁堆
void DostroyHeap(Heap* hp)
{
	assert(hp);
	if (hp->_array)
	{
		free(hp->_array);
		hp->_capacity = 0;
		hp->_size = 0;
	}
}