【图像处理】Seam Carving for Content-Aware Image Resizing

摘要

高效的图像放缩还需要考虑图像的内容，作者提出的方法是一种称为seam carving的简单图像操作，可以实现content-aware的图像放缩。其中，seam是一张图像从上到下或从左到右上一条可选的八连接像素路径，由图像能量函数定义。通过不断地切开或连接seam，通过在各个方向应用这个操作可以将图像放缩到一个新的尺寸。seam的选择与顺序可以保留图像基于能量函数定义的内容。seam carving同样可以用于图像内容增强和物体移除。作者的方法支持各种定义能量图像的可视化评价方式，并且可以通过用户的输入进行引导。通过存储图像中seam的顺序作者创建了多尺度图像，能够实时作出持续的改变。

1、Introduction

如今各种呈像设备与方式五花八门，因此图像的放缩十分重要。然而一般的放缩往往是难以满足要求的，只考虑了对几何的限制。作者提出了一种简单的图像操作，即seam-carving，能够给予图像内容更好地考虑图像的结构。尽可能地删掉低能量部分，保留高能量部分。
作者还证明了其提出的方法可以用于纵横比、图像重定位、图像增强和物体移除。并且，通过加上seam移除和连接在纵横方向的顺序，作者定义了多尺度图像。这些图像可以通过考虑内容的方式持续的改变。
seam carving支持多种能量函数，例如梯度幅度、交叉熵、视觉显著性等。这些连接与移除是参数无关的。另外作者还提供了用户界面。
作者的主要贡献如下：

• 定义了seam carving并且展现了它的特性
• 呈现了通过seam连接的数据增强算法
• 使用seam用于content-aware的图像尺寸操作
• 微连续图像重定位定义多尺度图像

2、Background

3、The Operator

作者的方法是使用一种明断的方法来移除像素。因此，问题在于如何选择移除的像素。直观的，作者的目标是去除与周围环境融合的不可见像素。因此就有了下面比较简单的能量函数。

给定一个能量函数，假定我们需要降低图像的宽度。有很多策略来实现。例如，一个维持能量的最优的策略是通过升序来移除像素。这会损坏图像的矩形形状，因为我们可能在每一行移除不同数量的像素。如果想避免这个则需要在每一行移除相同数量低能量的像素。但是这样会产生锯齿效应。为了保持图像的形状和视觉一致性，可以使用自动裁剪。即寻找一个子窗口，即目标图像的尺寸包括最高的能量。另一个可行的策略是移除最低能量的整列，然而结果图像中可能会出现artifacts。因此，需要一个比crop和column removal更少约束的resize方法，能够比一般的像素移除方法更好地保留图像内容。即有来本文通过定义内部seam实现的方法。

这表示的是一条垂直路径，每行包含一个像素。相应的是水平路径：

seam上的像素类似于移除一行或一列会有一个局部作用，所有的像素会被向左或向上移动来弥补这条路径。视觉上只有这条seam上的路径有可视化影响，图像的其他部分上完整的。这里约束中的小于等于1也可以根据需要替换微小于等于k。当k等于0的时候即一条垂直或水平的路径。
给定一个能量函数e，可以定义seam上的损失，即路径上所有像素值损失的累加。我们需要寻找的即能够最小化这个cost的最优路径。这个最优路径可以通过动态规划来实现。第一步是遍历图像从第二行到最后一行并且计算所有可能过的累计的最小能量M：

这个过程的最后，最后一行的最小值是这段相连的纵向路径的终点。因此第二步通过回溯来找到最优seam，横向的也类似。

3.1 Energy Preservation Measure

为了评估不同策略的效率，可以检测放缩过程中图像中所有像素的平均能量。随机移除像素应该不改变这个平均值，但是content-aware裁剪在移除的过程中应该提高这个平均值，因为它移除低能量像素，保存高能量像素。

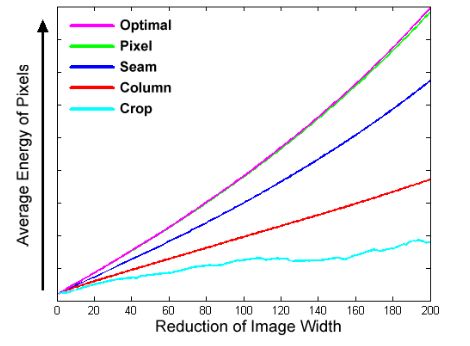
这张图表现来各种方法缩小宽度后平均像素能量的变化。正如预期的，移除最低能量像素的情况给出来最优解，与像素移除方式结果类似，但是这两个方法都损坏了图像的可视化一致性。crop的效果最差，移除列要好了一些但是仍然造成来artifacts。本文提出的seam carving表现出在保持视觉一致性与平均像素能量的最优效果。这个图表的规律对于大多数图像都适用。

3.2 Image Energy Functions

作者尝试来多种图像重要性判j据，包括L1、L2范数、显著性判据、Harris角点判据，也尝试了注视方向判据以及人脸检测的输出。


事实上，没有一个判据在缩所有图像上表现都很好，但是一般来说它们都表示了一个类似的放缩范围。作者发现e1和ehog表现都不错。

4、Discrete Image Resizing

4.1 Aspect Ratio Change

假如说要把图像从过年n ✖️ m转为n ✖️m‘，其中m - m’ = c，可以通过移除c条纵向seam实现。与简单的缩放不同，这个操作不会改变图像的关键部分。

4.2 Retargeting with Optimal Seams-Order

图像重定向对于比例的改变从一维到了两维，为了方面介绍假设新的n与m都比原来小。这个问题在于seam carving的正确顺序是什么？先移动哪条横向边还还是水平边或是在两者之间转换。作者将这个最优顺序的搜索定义为下面的函数的优化问题：

这个式子还是比较好理解的，一个E的累加最小值，k是横纵差的和，每次移除横向还是纵向根据阿尔法的取值。
具体实现使用了一个映射T(r, c)，表示将尺寸缩小为n - r ✖️ m - c需要的最小cost。使用动态规划计算。

4.3 Image Enlarging

图像放大即在图像中加入seam。计算最优的横向或纵向seam然后通过与周围的像素平均复制这些像素。但是效果会比较差，类似于上图中的（b）。为了实现增大图像的目的，需要对原始图像内容和插入的部分做一个比较好的平衡。因此选择k个seam进行移除，然后再复制它们。这个可以看作是缩小图像的一个逆过程，恢复一个虚拟的更大图像中被删除的seam。
复制所有的seam相当于标准的放缩，如上图中的e。巍峨了实现一个content-aware方式，作者将这个过程分解。每一步都不会将图像的大小放大超过上一步的一小部分，保证关键部分得到了拉伸。但不管怎么样，较大的放大还是会产生一些人造的痕迹。

4.4 Content Amplification

seam carving还可以在保持原尺寸的情况下增大图像中的内容。可以通过seam carving与放缩合并来实现。为了尽可能保持图像的内容，作者首先使用标准的放缩来放大图像，然后通过carving seam将其缩小为原来的尺寸。

4.5 Seam Carving in the gradient domain

经常在移除多条seam的时候会有一些明显的视觉上人造的痕迹，为了克服这个问题可以将seam carving与Poisson重建合并。可以仍然通过之前的方式计算能量函数，但是并不移除seam，而是在梯度域从图像x和y倒数的方向移除。然后再使用poisson solver重构图像。

4.6 Object Removal

作者设计来一个gui，用户可以将需要移除的物体标记，然后系统会移除seam直到标记的部分完全消失。系统可以自动地进行横向和纵向seam移除，为了保持原有的图像大小还需要进行一定的填充，相比于之前的方法，这个方法在全局进行修改，因为seam可能在任何地方。

5、Multi-size Images

至今为止的各种方法都是假设用户提前知道目标尺寸，但很多时候这个是不现实的。
seam carving对于像素是线性的并且resize中插入或删除的seam也是线性的。平均来说，比如将400 ✖️ 500缩放为100 ✖️ 100，然而实时计算这么多seam是一个具有挑战性的任务。为了处理这个问题，作者提出来一种多尺度编码。这个信息的内存占用量很低，可以在预处理阶段很快的完成，并且允许用户实时地对图像进行持续标定。
从另一个角度看，这可以看作是存储了一个显式的时间演化隐含过程的seam移除和插入。首先，定义了一个n ✖️ m的index map V，用来存储某一个像素被哪一条seam移除了。为了获得一个m‘宽度的图像，只需要收集所有像素值大于等于m - m’的像素。
这个表示方式支持图像扩大也支持图像缩小。例如，如果想要支持将图像扩大到M’，这个过程其实与缩小类似，不过其存储的为负值，仍然可以通过大小选择插入哪些seam。
计算一个垂直index map H与之类似。然后独立地计算H和V来支持多尺度resize是不可行的，这是因为两者会发生许多冲突，以及在一个方向移除seam可能会损坏另一个方向的index map。

6、Limitations

作者的方法其实并不是在所有的图像上都能自动完成，需要加入一些更高层的信息。例如上图中使用e1 error function的效果不好，还需要结合人脸检测器。下图是一个加入用户约束的例子。

有的时候，高层信息甚至也无法解决，可以以两种主要的因素为特征来限制seam carving。第一个是图像中内容的数量。如果这个图像太密集，那么并不包含不太重要的区域，因此各种content-aware的方法效果都不好。第二个约束是图像内容的布局。在某些类型的图像，图像可能不是很密集，但是内容被布局为一种seam难以避开重要的部分。

7、Conclusions and Future Work

作者提出了一种content-aware的放缩操作，即seam carving。seam是在图像中的最优路径，将会被移除或插入到一张图像中。这个操作可以用于各种图像处理的问题中，并且能够与很多指标合并。另外，作者还定义了一种支持多尺度图像实时处理的数据结构。这里还有很多可以做的工作，作者希望能够将其方法扩展到其他领域，例如视频放缩。作者还想去将scale和resize合并，并且定义更多的鲁棒的图像，以及寻找一个合并多尺度图像中横向和纵向seam更好的方法。

总结

这篇文章还是比较早的，也是比较经典的图像处理方法，里面也用到来动态规划等计算机学科特点比较鲜明的方法。创新点在我看来主要是基于已有的一些成果进一步去思考怎么能尽可能避免可视化不合理的效果来对图像进行放缩。这里的思路也是比较自然，重要的部分保留，不重要的部分选择性处理。作者进一步思考这个问题，借助能量函数作为评判，当然这里我觉得还可以用别的方法评判，也许会得到更好的方法。说白来还是遇到问题解决问题，思路本身并不是超前的让人无法接受，而且本身也确实存在一些无法避免的局限性。有了seam carving这个基本方法，便可以思考更多的应用，比如图像增强等等。另外作者使用的多尺度映射实际上是一种用空间换时间的做法。