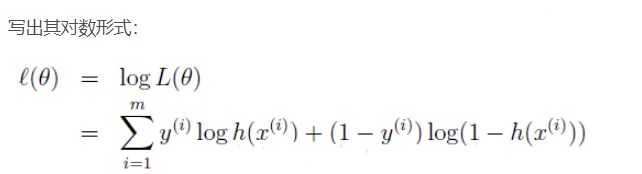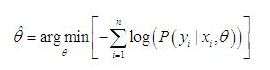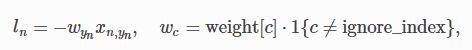深度学习基础知识（六）--- 损失函数

 

1.L1损失（绝对损失函数） 和 L2 损失（平方损失函数）

L1范数损失函数，也被称为 最小绝对值偏差（LAD），最小绝对值误差（LAE）。

总的说来，它是把目标值（Yi）与估计值（f(xi)）的绝对差值的总和（S）最小化：

 

L2范数损失函数，也被称为最小平方误差（LSE）。总的来说，它是把目标值（Yi）与估计值（f(xi)）的差值的平方和（S）最小化：

2. MSE-loss（Mean Square Error）均方误差

先求差的平方、再求和、再求平均

一般用于解决回归问题

解决回归问题的神经网络一般只有一个输出节点，这个节点的输出值就是预测值。

3. CrossEntropy-loss 交叉熵 损失函数

损失函数定义如下

交叉熵损失函数从 logistic回归讲起

logistic回归实际上是在做二分类，也即0，1分类

它的函数形式为：

这个函数其实就是 sigmoid函数形式，

 

 

对数似然函数：

 

现在想要对其取极大值，（因为是极大似然估计），

那么在前面加个负号，求其最小值即可，(神经网络中一般用梯度下降求最小值)：

这就是CrossEntropy loss的形式了

 

当上式的 h(x) 是 sigmoid函数的时候，就也称为BCE ---（ Binary Cross Entropy） 二元交叉熵

一般用于二分类问题

附上pytorch的 BCE loss 函数 的链接： https://pytorch.org/docs/0.4.1/nn.html#bceloss

 

如果我们希望处理多分类问题，那么h(x)换成 softmax函数就ok， softmax函数为：

可参考pytorch 交叉熵损失函数：

https://pytorch.org/docs/0.4.1/nn.html#crossentropyloss

这里说一下，它采用的公式是：

这是因为在算损失的时候，它相当于直接令 y=1来算损失，

也就是 上面交叉熵损失公式中，后面那一部分直接为0，只保留了前部分。

因为多分类的时候，并不是y=0或y=1这两种情况，而是y=1到 k 这种情况，

只不过采用one hot 编码时，每个类的标签都为1，但是所处位置不同而已，所以在多分类的情况，其实没有 y=0这部分出现。

4. NLL-loss（Negative Log Liklihood） 负对数似然概率

在pytorch的交叉熵损失函数定义中，有这么一句话：

交叉熵损失 是将 Logsoftmax 和 NLLLoss结合到一起了,

也就是说 NLLLoss 要求的输入是 对数似然概率，log-probabilities， 也就是应接受 Logsoftmax的结果，它本身的定义为：

但是由于pytorch中指定它接受的已经是经过Logsoftmax处理过的数据，所以实际的运算为：

 

即对输入的Logsoftmax数据前面乘上一个权重然后求负数，再对batchsize 求和（最多再取个平均）

5.BCEwithlogits-loss

BCEWithLogitsLoss就是把Sigmoid-BCELoss合成一步

不然的话，使用BCEloss就是要先对数据进行 sigmoid函数操作，

然后将结果再输入BCELoss求损失值，

有点类似于pytorch本身的CrossEntropyLoss将 Logsoftmax 和 NLLLoss结合在一起了

 

6.SmoothL1-loss

多用于目标检测，比如Fast R-CNN

对于边框的预测是一个回归问题。

通常可以选择平方损失函数（L2损失）f(x)=x^2。但这个损失对于比较大的误差的惩罚很高。

我们可以采用稍微缓和一点绝对损失函数（L1损失）f(x)=|x|，它是随着误差线性增长，而不是平方增长。

但这个函数在0点处导数不存在，因此可能会影响收敛。

一个通常的解决办法是，分段函数：

在0点附近使用平方函数f(x)=x^2 使得它更加平滑。其余位置使用 f(x)=|x|使它增长缓慢

它被称之为平滑L1损失函数。它通过一个参数sigma来控制平滑的区域。

                                                  图源  https://zhuanlan.zhihu.com/p/48426076