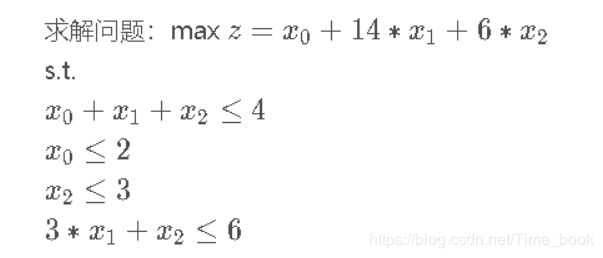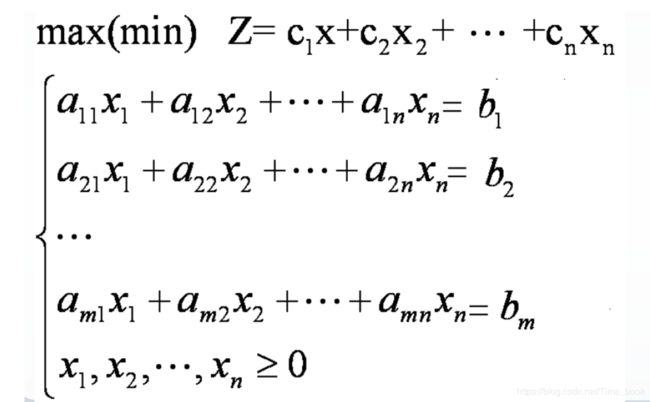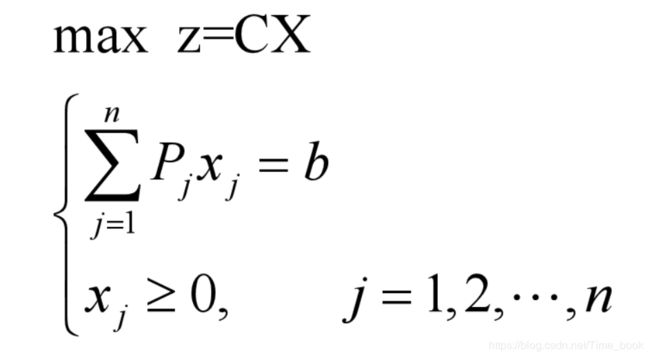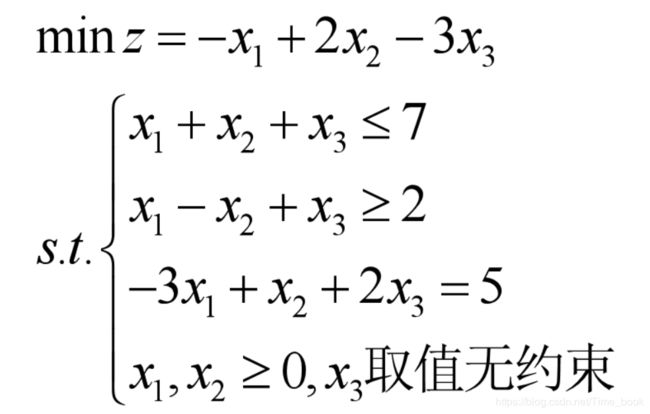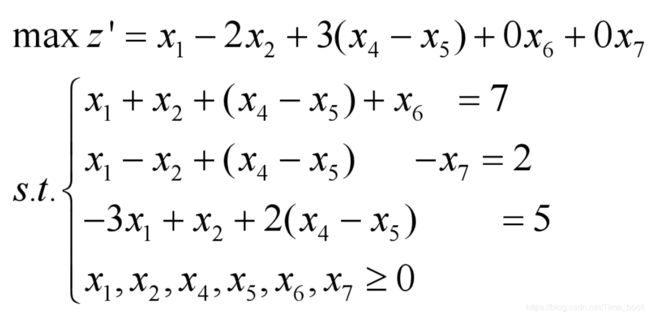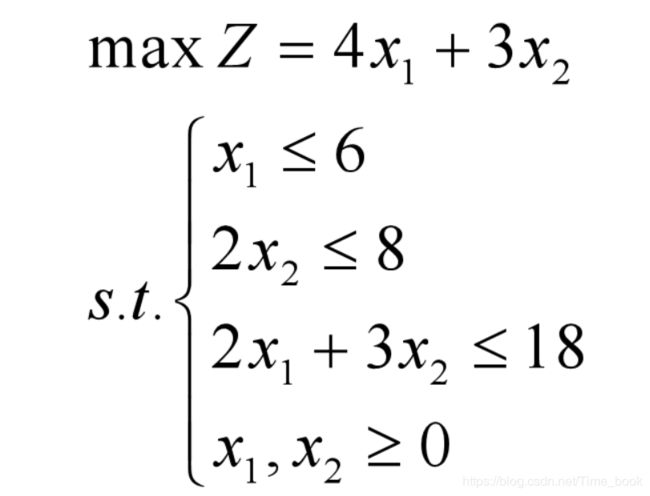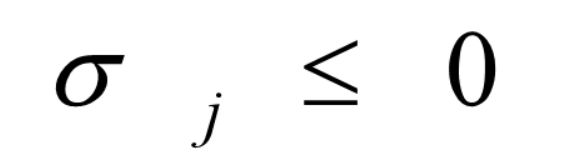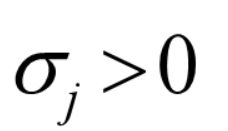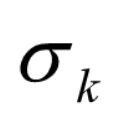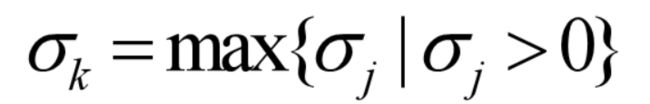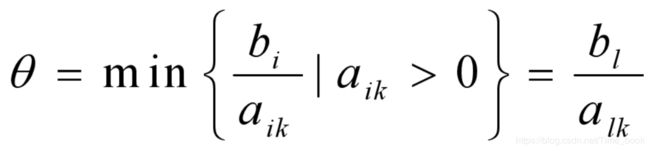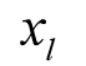python单纯形法求解线性规划问题

单纯形法求解线性规划问题

概念

线性规划（Linear programming），是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支，它是辅助人们进行科学管理的一种数学方法。研究线性约束条件下线性目标函数的极值问题的数学理论和方法。英文缩写LP。

数学模型

（1）列出约束条件及目标函数

（2）画出约束条件所表示的可行域

（3）在可行域内求目标函数的最优解及最优值

线性规划的标准型一般形式为：

这里规定的标准形式为：

1.目标函数的要求是max

2.约束条件的要求是等式

3.决策变量的要求是非负约束

4.在标准型式中规定各约束条件的右端项bi≥0，否则等式两端乘以“-1”。

用向量和矩阵符号表述时为：

称A为约束条件的m×n维系数矩阵，一般m0;

b为资源向量；

C为价值向量；

X为决策变量向量。

下面举个例子：

将下述线性规划化标准型

而变换方法如下：

最终我们还是需要回归到实际应用中

我们用中学时简单的线性规划来看一下如何解决实际问题的

图解法求解

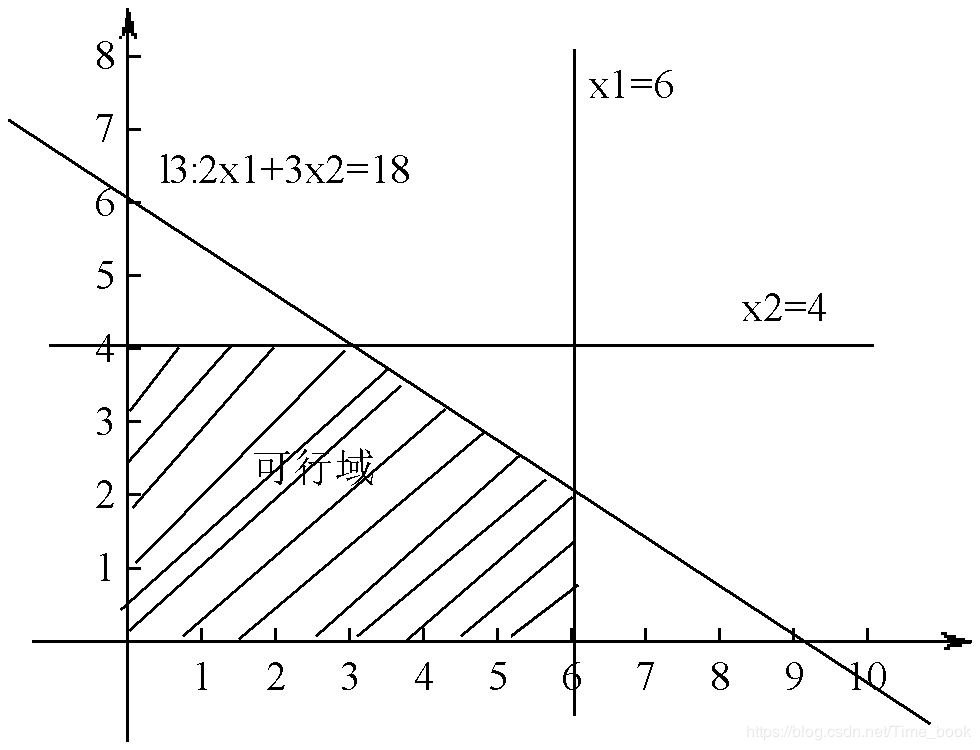
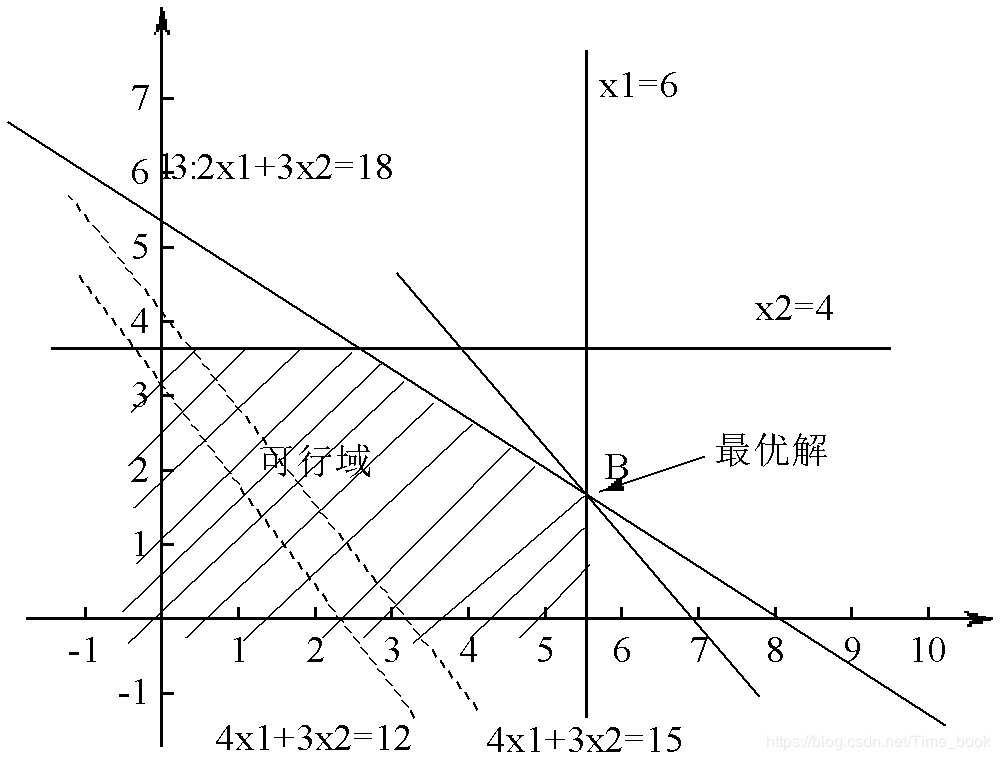
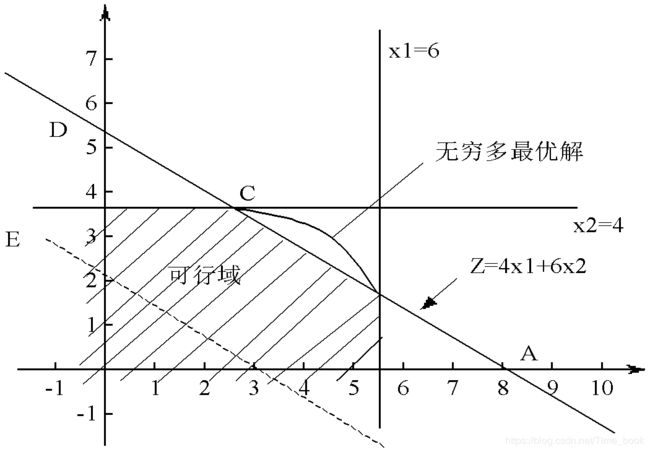
无穷多最优解。若将上例中的目标函数变为求max Z=4x1+6x2，则目标函数与等值区域边界线2x1+3x2=18平行，线段BC上的任意一点都使Z取得相同的最大值，此时线性规划问题有无穷多最优解，如下图所示：

说了这么多，还是回到主题单纯形法上来

一般线性规划问题中当线性方程组的变量数大于方程个数，这时会有不定数量的解，而单纯形法是求解线性规划问题的通用方法。

所以下面来点干货

单纯形法的计算步骤

第一步：求出线性规划的初始基可行解，列出初始单纯形表。

第二步：进行最优性检验。各非基变量检验数为

则表中的基可行解是问题的最优解，计算到此结束，否则进入下一步。

第三步：在

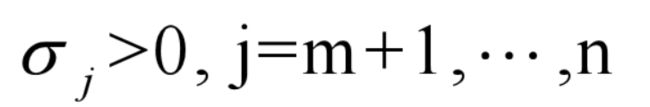中，若有某个

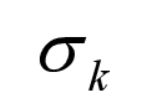
对应xk的系数列向量Pk≤０，则此问题无界，停止计算。否则，转入下一步。

第四步：从一个基可行解换到另一个目标函数值更大的基可行解，列出新的单纯形表。
确定换入变量，有

对应的变量xj就可作为换入变量，当有两个以上检验数大于零，一般取最大的

即

取xk 作为换入变量。

确定换出变量。根据最小θ规则，对Pk列由公式计算得:

确定是 换出变量。

元素aik决定了从一个基本可行解到另一个可行解的转移去向，取名为主元素。以aik 为主元素进行旋转变换，得到新的单纯形表，转到步骤二。

下面是代码演示：

import numpy as np

# d数组第0行是c，最后一列是b，其余是A

def pivot():
    l = list(d[0][:-1]) # 
    jnum = l.index(max(l)) #转入编号
    m = []
    for i in range(bn):
        if d[i][jnum] == 0:
            m.append(0.)
        else:
            m.append(d[i][-1]/d[i][jnum])
    inum = m.index(min([x for x in m[1:] if x!=0]))  #转出下标
    s[inum-1] = jnum #更新基变量
    #更新d
    r = d[inum][jnum]
    d[inum] /= r
    for i in [x for x in range(bn) if x !=inum]:
        r = d[i][jnum]
        d[i] -= r * d[inum]
        
def solve():
    flag = True
    while flag:
        if max(list(d[0][:-1])) <= 0: #直至所有系数小于等于0
            flag = False
        else:
            pivot()
            
def printSol():
    for i in range(cn - 1):
        if i in s:
            print("x"+str(i)+"=%.2f" % d[s.index(i)+1][-1])
        else:
            print("x"+str(i)+"=0.00")
    print("objective is %.2f"%(-d[0][-1]))

d = np.loadtxt("F:/人工智能与机器学习/data.txt", dtype=np.float)
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) #基变量列表
solve()
printSol()

x0=0.00
x1=1.00
x2=3.00
x3=0.00
x4=2.00
x5=0.00
x6=0.00
objective is 32.00

data.txt

1 14 6 0 0 0 0 0

1 1 1 1 0 0 0 4

1 0 0 0 1 0 0 2

0 0 1 0 0 1 0 3

0 3 1 0 0 0 1 6

optimize包

from scipy.optimize import linprog

C = [-1,-14,-6] 
A = [[1,1,1],[0,3,1]]
b = [4,6]
X0_bounds = [None,2]
X1_bounds = [None,None]
X2_bounds = [None,3]
res = linprog(C,A,b,bounds=(X0_bounds,X1_bounds,X2_bounds))
print(res)

     con: array([], dtype=float64)
     fun: -31.999999992607634
 message: 'Optimization terminated successfully.'
     nit: 4
   slack: array([1.89428917e-09, 1.10320819e-09])
  status: 0
 success: True
       x: array([-8.09045719e-10,  1.00000000e+00,  3.00000000e+00])

所以最优解为31.999999992607634

单纯形法的优点：计算简单，不需要求函数（偏）导数，可以没有函数的解析式，只要有函数值即可应用

缺点：收敛速度慢

适合场合：各种无约束问题

单纯形法的最坏时间复杂度为指数级别

参考文章

https://wenku.baidu.com/view/eecfcc29ed630b1c59eeb52c.html

https://blog.csdn.net/kittyzc/article/details/81707464