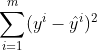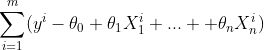机器学习-梯度下降法详解及实现
梯度下降法
概念
梯度下降法是迭代法的一种,其实它不是一种具体的机器学习算法,是一种基于搜索的最优化方法,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。相应的还有一个梯度上升法,它的作用是最大化一个效用函数。
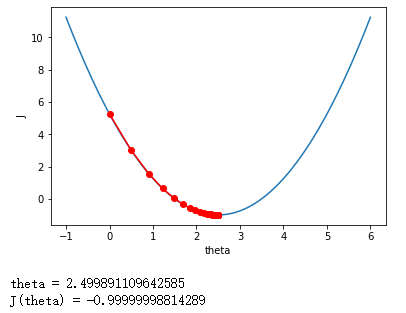
用一个图来表示梯度下降法
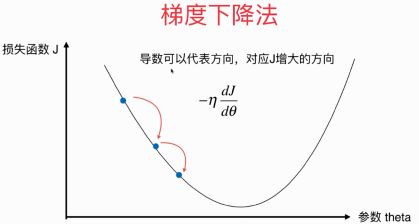
怎么理解呢?梯度其实是在在多维空间中的概念,在二维的平面上其实就是导数,梯度表示的就是方向,通过求某一个点的梯度,我们就可以知道J(损失函数)增大的方向,然后乘-η就可以找到J(损失函数)减小的方向,不断地求J的导数,直到其变为0,这样就找到J的最小值点。这里的η称为学习率,η的取值影响获得最优解的速度,η取值太小的时候学习速度收敛太慢,η太大有可能直接跳过最小值点然后导致不收敛。
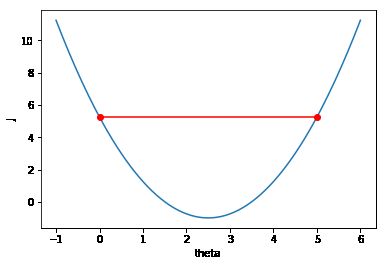
并不是所有的函数都有唯一的极值点,例如
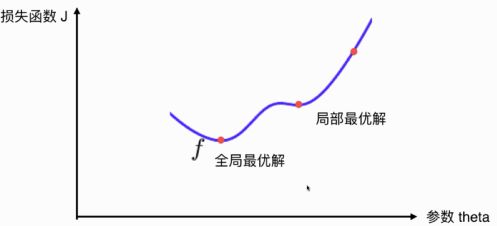
有可能在某一次取值的过程中找到的是局部最优解,而不是全局最优解。这个时候怎么解决呢?多次运行,随机化初始点,这样的话增加了找到全局最优解的概率。
模拟实现梯度下降法
jupyter notebook中实现:
import numpy as np
import matplotlib.pyplot as plt
#datasets
x = np.linspace(-1, 6 ,141)
y = (x-2.5)**2-1
# 求导数
def dJ(theta):
return 2*(theta - 2.5)
# 损失函数
def J(theta):
return (theta - 2.5)**2-1
# 梯度下降法
theta = 0.0
eta = 0.1
#误差精度
epsilon = 1e-8
theta_history = [theta]
while True:
gradient = dJ(theta)
last_theta = theta
theta = theta - eta * gradient
theta_history.append(theta)
if(abs(J(theta) - J(last_theta)) < epsilon):
break
plt.plot(x, y)
plt.plot(np.array(theta_history), J(np.array(theta_history)), color='R', marker = 'o')
plt.xlabel("theta")
plt.ylabel("J")
plt.show()
print("theta = " + str(theta))
print("J(theta) = " + str(J(theta)))
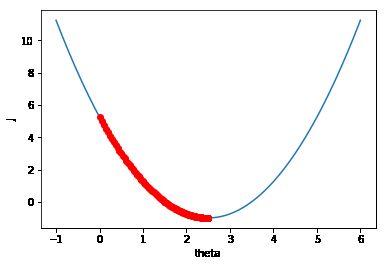
然后我们上面讨论过,η取值太小的时候学习速度收敛太慢,η太大有可能直接跳过最小值点然后导致不收敛。下面测试一下。先取η=0.01
当η>1的时候编译器就自动报错,但是这里只是针对这里定义的这个函数,并不是意味着η=1就是极限值,针对不同的函数有不同的取值。
多元线性回归中使用批量梯度下降
尽可能小,而且线性回归算法的损失函数是具有唯一解的。
其中
![]()
批量梯度下降法具体实现
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
x = 2 * np.random.random(size = 100)
y = x * 3.0 + 4.0 + np.random.normal(size = 100)
X = x.reshape(-1, 1)
#损失函数
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta))**2)/len(X_b)
except:
return float('inf')
#损失函数的梯度
def dJ(theta, X_b, y):
res = np.empty(len(theta))
res[0] = np.sum(X_b.dot(theta) - y)
for i in range(1, len(theta)):
res[i] = (X_b.dot(theta) - y).dot(X_b[:,i])
return res *2 /len(X_b)
#梯度下降法
def gradient_descent(X_b, y, initial_thata, eta, n_iters = 1e4, epsilon = 1e-8):
theta = initial_theta
i_iter = 0
while i_iter < n_iters:# n_iters是最大循环次数
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
i_iter += 1
return theta
X_b = np.hstack([np.ones((len(x), 1)), x.reshape(-1, 1)])
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01
theta = gradient_descent(X_b, y, initial_theta, eta)
plt.scatter(x, y)
Y = X_b.dot(theta)
plt.plot(x, Y, color="red")
plt.show()
print("theta = " + str(theta))
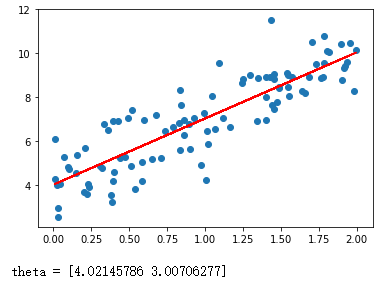
得到的结果
在初始化数据的时候,斜率设为3,截距为4,然后我们训练出的结果theta与两值接近,证明训练的模型是准确的:
y = x * 3.0 + 4.0 + np.random.normal(size = 100)
随机梯度下降法
上面我们用的是批量梯度下降法,这种方法有一个缺点,就是每一项都需要对所有的样本点进行计算,数据量少的时候还可以,但是数据量很大的时候就显得很鸡肋了,计算非常的耗资源。能不能每一次计算的时候只对其中的一个样本进行计算呢?这就衍生出了随机梯度下降法。
即每读取一条样本,就迭代对Θ进行更新,然后判断其是否收敛,若没收敛,则继续读取样本进行处理,如果所有样本都读取完毕了,则循环重新从头开始读取样本进行处理。但是,相较于批量梯度下降算法而言,随机梯度下降算法使得J(Θ)趋近于最小值的速度更快,但是有可能造成永远不可能收敛于最小值,有可能一直会在最小值周围震荡,但是实践中,大部分值都能够接近于最小值,所以当数据量很大的时候可以用精度来换取时间。
在随机梯度下降法中为了得到更高的收敛结果,学习率是要随着循环次数的增加而逐渐的减小。这是因为在学习的过程中要是学习率是一个固定值,但是可能由于随机的过程不够好,eta有是一个固定值,那么在学习的过程中随机梯度下降法接近最优解的时候又会慢慢的跳出最优解的范围。气质学习率随着循环次数的增加而逐渐的减小这种思想是模拟退火的思想,去搜了下模拟退火,下面写下自己的理解。
模拟退火算法
模拟退火其实也是一种贪心算法,但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解,因此有可能会跳出这个局部的最优解,达到全局的最优解。
模拟退火算法描述:
想象一个高温物体的降温过程。其温度为T时出现能量差为dE的降温概率为
P(dE) = e ^ ( -dE / (k * T) ) 。
其实就是温度越高降温的概率越大,温度越低降温概率越小。而模拟退火就是利用这样一种思想去进行搜索。
那么在进行搜索的时候首先定义一个初始值( 温度 ) T , 一个系数 r ( 降温速度 0 < r < 1 ) , 假设你当前状态为 f i , 你的下一个状态为 f i +1 , 对这两个状态进行评价,如果更接近你想要的结果,就更新到这个状态,否则则以 P ( dE ) 的概率去更新到 这个状态,但是其实在实际题目中,这个概率是不必要的,这一步有时是可以忽略掉的。我们可以想象,随着搜索次数的不断增多,搜索范围将越来越趋近于稳定,也就是随着时间的增长温度降低的概率越来越低,直到趋近于1。对应搜索就是随着你搜索的次数越多,你搜索到的值是你想要的值的概率就越大。
其中i_iters是循环次数,a,b是两个经验参数,根据实际情况设置。
看完了梯度下降法,其优缺点如下:
第一种,遍历全部数据集算一次损失函数,然后算函数对各个参数的梯度,更新梯度。这种方法每更新一次参数都要把数据集里的所有样本都看一遍,计算量开销大,计算速度慢,不支持在线学习,其实这就是批量梯度下降。
另一种,每看一个数据就算一下损失函数,然后求梯度更新参数,这个其实也就是随机梯度下降,这个方法速度比较快,但是收敛性能不太好,可能在最优点附近晃来晃去,找不到不到最优点。两次参数的更新也有可能互相抵消掉,造成目标函数震荡的比较剧烈。
为了克服两种方法的缺点,现在一般采用的是一种折中手段,小批的梯度下降,这种方法把数据分为若干个批,按批来更新参数,这样,一个批中的一组数据共同决定了本次梯度的方向,下降起来就不容易跑偏,减少了随机性。另一方面因为批的样本数与整个数据集相比小了很多,计算量也不是很大。
随机梯度下降法实现
import numpy as np
import matplotlib.pyplot as plt
m = 100000
x = np.random.normal(size = m)
X = x.reshape(-1, 1)
y = 4.0 * x + 3.0 + np.random.normal(0 ,3, size = m)
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta))**2) / len(y)
except:
return float('inf')
def dJ_sgd(theta, X_b_i, y_i):
return X_b_i.T.dot(X_b_i.dot(theta) - y_i) * 2.0
def sgd(X_b, y, initial_theta, n_iters):
t0 = 5
t1 = 50
def learning_rate(t):
return t0 / (t + t1)
theta = initial_theta
for cur_iter in range(n_iters):
rand_i = np.random.randint(len(X_b))
gradient = dJ_sgd(theta, X_b[rand_i], y[rand_i])
theta = theta - learning_rate(cur_iter) * gradient
return theta
X_b = np.hstack([np.ones((len(X), 1)), X])
initial_theta = np.zeros(X_b.shape[1])
theta = sgd(X_b, y, initial_theta, n_iters = len(X_b)//3)
print("theta = " + str(theta))
输出的theta = [3.00887864 4.05589554],与设置的数据相接近。