机器学习之线性回归（Linear Regression）

线性回归

概念

线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。
其特点为：
- 解决回归问题

• 思想简单，实现容易

• 许多强大的非线性模型的基础

• 结果具有很好的可解释性

• 蕴含机器学习中的很多重要思想

## 简单线性回归的实现

下面我们来举例何为一元线性回归分析:
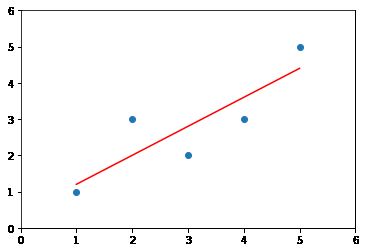
首先假设有这样一组数据

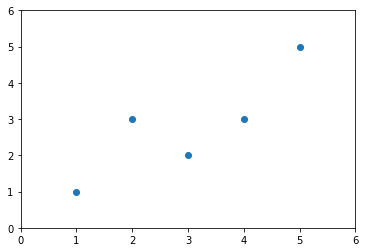
从数据中我们可以看出，可以找到一条直线实现数据的拟合，这条直线设为
y=ax+b
那怎么计算a和b的参数，公式如下:

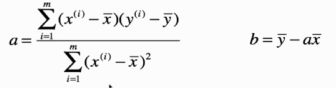
jupyter notebook中具体的代码实现：

x_mean = np.mean(x)
y_mean = np.mean(y)
#分子
num = 0.0
#分母
d = 0.0
for x_i, y_i in zip(x, y):
num += (x_i - x_mean) * (y_i - y_mean)
d += (x_i - x_mean) ** 2
a = num/d
b = y_mean - a*x_mean
y_hat = a*x + b
plt.scatter(x,y)
plt.plot(x,y_hat,color="r")
plt.axis([0,6,0,6])
plt.show()

得到了拟合数据的直线：

这里还可以在底层自己实现线性回归的算法，然后在jupyter notebook中调用，相应的pycharm的代码为：

import numpy as np
from sklearn.metrics import r2_score

class LinearRegression:

def __init__(self):
"""初始化Linear Regression模型"""
self.coef_ = None
self.intercept_ = None
self._theta = None

def fit_normal(self, X_train, y_train):
"""根据训练数据集X_train, y_train训练Linear Regression模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"

X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]

return self

def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
"""根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"

def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
except:
return float('inf')

def dJ(theta, X_b, y):
# res = np.empty(len(theta))
# res[0] = np.sum(X_b.dot(theta) - y)
# for i in range(1, len(theta)):
# res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
# return res * 2 / len(X_b)
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(X_b)

def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):

theta = initial_theta
cur_iter = 0

while cur_iter < n_iters:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break

cur_iter += 1

return theta

X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.zeros(X_b.shape[1])
self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]

return self

def fit_sgd(self, X_train, y_train, n_iters=5, t0=5, t1=50):
"""根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
assert n_iters >= 1

def dJ_sgd(theta, X_b_i, y_i):
return X_b_i * (X_b_i.dot(theta) - y_i) * 2.

def sgd(X_b, y, initial_theta, n_iters, t0=5, t1=50):

def learning_rate(t):
return t0 / (t + t1)

theta = initial_theta
m = len(X_b)

for cur_iter in range(n_iters):
indexes = np.random.permutation(m)
X_b_new = X_b[indexes]
y_new = y[indexes]
for i in range(m):
gradient = dJ_sgd(theta, X_b_new[i], y_new[i])
theta = theta - learning_rate(cur_iter * m + i) * gradient

return theta

X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.random.randn(X_b.shape[1])
self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)

self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]

return self

def predict(self, X_predict):
"""给定待预测数据集X_predict，返回表示X_predict的结果向量"""
assert self.intercept_ is not None and self.coef_ is not None, \
"must fit before predict!"
assert X_predict.shape[1] == len(self.coef_), \
"the feature number of X_predict must be equal to X_train"

X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return X_b.dot(self._theta)

def score(self, X_test, y_test):
"""根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

y_predict = self.predict(X_test)
return r2_score(y_test, y_predict)

def __repr__(self):
return "LinearRegression()"

​
这里其实就是一个简单的一元数据的一个简答线性回归算法。

线性回归评价指标

那怎么去评价线性回归算法的指标的好坏呢？
常用得三个指标：均方误差MSE、均方根误差RMSE、平均绝对误差MAE，这三类算法具体公式这些就不再赘述了，这三类指标都存在一个局限性：作用域的使用范围，对不同事物的预测缺乏统一标准，这样就引出了新的一个预测指标R Squared，其实就是R^2,关于R^2的解释如下：

从上面的图中我们到关于R^2的公式，公式中上面分子就是我们训练出的模型预测的所有误差。 下面分母就是 不管什么我们猜的结果就是y的平均数。（其实也就是我们瞎猜的误差）
那具体实现下这些评价指标，首先换一个数据集，上面是我们自己构造的的太简单了，
导入sklearn中的datasets

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error

boston = datasets.load_boston()
x = boston.data[:,5]
y = boston.target
x = x[y<50.0]
y = y[y<50.0]
plt.scatter(x, y)
plt.show()
# 划分训练集和测试集

x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.2)

# 简单线性规划
x_mean = np.mean(x_train)
y_mean = np.mean(y_train)
# 分子
num = 0.0
# 分母
d = 0.0
for x_i, y_i in zip(x_train, y_train):
num += (x_i - x_mean) * (y_i - y_mean)
d += (x_i - x_mean) ** 2
a = num/d
b = y_mean - a*x_mean
y_hat = a*x_train + b # 回归函数
plt.scatter(x_train, y_train)
plt.plot(x_train, y_hat, color="r")
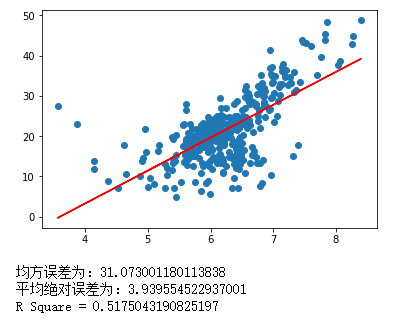
plt.show()

y_predict = a*x_test + b
mse = mean_squared_error(y_test, y_predict)
mae = mean_absolute_error(y_test, y_predict)
print("均方误差为：" + str(mse))
print("平均绝对误差为：" + str(mae))
rs = 1 - mse/np.var(y_test)
print("R Square = " + str(rs))

这样我们就得到了所有的评价指标。