关于线性表的几个考点专题

有序表的二路归并

(note:看清楚问题的要求，能否破坏原有表LA和LB，也就是归并后产生的新表能否利用LA或LB的空间)

1.顺序表的归并

      分别扫描LA和LB两个有序表，当两个有序表都没有扫描完时产生循环：比较LA、LB的当前元素，将其中较小的元素放入LC中，再从较小元素所在的有序表中取下一个元素。重复这一过程直到LA或LB比较完毕，最后将未比较完的有序表中余下的元素放入LC中。

此代码是要求不能破坏原有表LA和LB的：

void merge(SqList *LA,SqList *LB,SqList *&LC)
{
	int i=0,j=0,k=0;	//i、j、k分别作为LA、LB、LC的下标，k为LC中元素的个数
	LC=(SqList *)malloc(sizeof(SqList));
	LC->length=0;
	while (i<LA->length && j<LB->length)
	{	
		if (LA->data[i]<LB->data[j])
		{	
			LC->data[k]=LA->data[i];
			i++;k++;
		}
		else				//LA->data[i]>LB->data[j]
		{	
			LC->data[k]=LB->data[j];
			j++;k++;
		}
	}
	while (i<LA->length)	//LA尚未扫描完,将其余元素插入LC中
	{	
		LC->data[k]=LA->data[i];
		i++;k++;
	}
	while (j<LB->length)  //LB尚未扫描完,将其余元素插入LC中
	{	
		LC->data[k]=LB->data[j];
		j++;k++;
	} 
	LC->length=k;
}

此代码对是否可以破坏原有表LA和LB无要求：

void merge(SqList A,SqList B,SqList &c){
	if(A.length+B.Length>C.maxSize)
		return false;
	int i=0,j=0,k=0;	//i、j、k分别作为A、B、C的下标
	while (i<A->length && j<B->length){ //核心：循环，两两比较，小者存放入表C
		if(A.data[i]<=B.data[j])
			C.data[k++]=A.data[i++];
		else
			C.data[k++]=B.data[j++];
	}
	//A或B表中，还剩一个没有比较完的顺序表
	while(i<A.length)
		C.data[k++]=A.data[i++];
	while(j<B.length)
		C.data[k++]=B.data[j++];
	C.length=k;
	return true;
}

2.链表的归并

递增、递增归并成递增（尾插法）
假设有两个按元素值递增次序排列的线性表A、B，均以单链表形式存储。请编写算法将这两个单链表归并为一个按元素值递增次序排列的单链表C，并要求用原来两个单链表的结点存放归并后的单链表

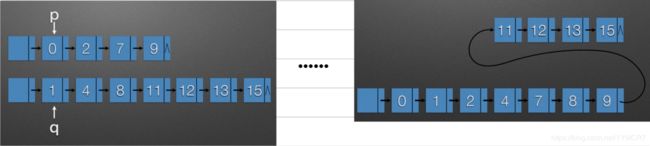
此代码是要求不能破坏原有表LA和LB的：

void merge(LinkNode *LA,LinkNode *LB,LinkNode *&LC)
{
	LinkNode *pa=LA->next,*pb=LB->next,*pc,*s;
	LC=(LinkNode *)malloc(sizeof(LinkNode));		//创建LC的头结点
	pc=LC;							//pc始终指向LC的最后一个结点
	while (pa!=NULL && pb!=NULL)
	{	
		if (pa->data<pb->data)
		{	
			s=(LinkNode *)malloc(sizeof(LinkNode));//复制pa结点
			s->data=pa->data;
			pc->next=s;pc=s;		//采用尾插法将结点s插入到LC的最后
			pa=pa->next;
		} 
		else
		{	
			s=(LinkNode *)malloc(sizeof(LinkNode));//复制pb结点
			s->data=pb->data;
			pc->next=s;pc=s;		//采用尾插法将结点s插入到LC的最后
			pb=pb->next;
		}
	}
	while (pa!=NULL)
	{	
		s=(LinkNode *)malloc(sizeof(LinkNode));	//复制pa结点
		s->data=pa->data;
		pc->next=s;pc=s;		//采用尾插法将结点s插入到LC的最后
		pa=pa->next;
	}
	while (pb!=NULL)
	{	
		s=(LinkNode *)malloc(sizeof(LinkNode));	//复制pa结点
		s->data=pb->data;
		pc->next=s;pc=s;		//采用尾插法将结点s插入到LC的最后
		pb=pb->next;
	}
	pc->next=NULL;
}

此代码对是否可以破坏原有表LA和LB无要求：

void merge(LNode *A,LNode *B,LNode *&C)
{
	LNode *p=A->next;//p指针来跟踪A的最小值结点
	LNode *q=B->next;//q指针来跟踪B的最小值结点
	LNode *r;//r始终指向C的末端
	C=A;//用A的头结点来做C的头结点，当然用B做也是可以的喽
	C->next=null;//
	free(B);//那B的头结点就没用用处了，一个光杆司令，把它释放掉
	r=C;//此时C是仅有头结点的空链表，头结点即为末端结点
	while(p!=NULL&&q!=NULL)//当p与q都不为空时，选取p与q所指结点中的最小值插入C的尾部
	//尾插法
	if(p->data<=q->data)
		{
			r->next=p;
			p=p->next;
			r=r->next;
		}
		else
		{
			r->next=q;
			q=q->next;
			r=r->next;
		}
	}
	r->next=null;
	//以下两句直接将还有剩余的链表连接在C的尾部
	//类比生活中接链子，是不是仅需从断掉的地方直接连起来就行了
	if(p!=NULL)
		r->next=p;
	if(q!=NUll)
		r->next=q;
}

递增、递增归并成递减（头插法）

void mergeR(LNode *A,LNode *B,LNode *&C)
{
	LNode *p=A->next; 
	LNode *p=A->next; 
	LNode *s;//s用来接收新的结点
	C=A; 
	C->next=null;
	free(B);
	while(p!=NULL&&q!=NULL)
	//头插法
	if(p->data<=q->data)
		{
			s=p;
			p=p->next;
			s->next=C->next;
			C->next=s;  //官话：指针的维护
		}
		else
		{
			s=q->data;
			q=q->next;
			s->next=C->next;
			C->next=s;
		}
	}
	//下面对于处理其中一个链表的剩余情况就和前面不一样了,只能再来头插蛮
	while(p!=NULL)
	{
		s=p;
		p=p-next;
		s->next=C-next;
		C-next=s;	
	}
	while(q!=NULL)
	{
		s=q-data;
		q=q-next;
		s->next=C-next;
		C->next=s;
	}
}

以上顺序表及单链表的二路归并算法的时间复杂度为：O((Length(LA)+Length(LB))

对于空间复杂度，如果是重新创建表就为：O((Length(LA)+Length(LB))，若产生的新表可以利用原有表LA或LB的空间，则为：O(1).

note：两个长度分别为m，n的有序表A和B采用二路归并算法，最好情况元素的比较次数：min(m,n)；最坏情况元素的比较次数为：m+n-1。

逆置问题

1.顺序表逆置

void Reverse(SqList &L){
	ElemType temp;       //中间变量倒手
	for(i=0;i<L.Length/2;i++)
	//交换L.data与L.data[L.length-i-1]
	temp=L.data[i];
	L.data=[i]=L.data[L.length-i-1];
	L.data[L.length-i-1]=temp;
}

2.单链表的原地逆置（头插法）

思想:将头结点摘下，然后从第一个结点开始，依次插入到头结点后面的结点(头插法建立单链表,直到最后一个结点为止）

LinkList Reverse(LinkList L){
	Lnode *p,*r; //p为工作指针，r用来保存p的后继，防止断链
	p=L->next;
	L-next=NULL;		//把头结点先摘下来
	while(p!=NULL){		//依次将后面的元素结点摘下来
		r=p->next;		//暂存p的后继
		p->next=L->next;//将p结点插入到头结点后面
		L->next=p;		//头结点与新插入的结点连起来
		p=r;			//p指向r所指的结点
	}
	return L;
}

顺序表的划分问题

母版：以第一个元素为枢轴，小于等于枢轴的元素在枢轴前面，大于枢轴的元素在枢轴后面

解法一：主要采用交换

void partition(SqList *&L)
{	int i=0,j=L->length-1;
	ElemType pivot=L->data[0];			//以data[0]为枢轴
	while (i<j)						//从区间两端交替向中间扫描,直至i=j为止
	{	while (i<j && L->data[j]>pivot)
			j--;						//从右向左扫描,找一个小于等于pivot的元素
		while (i<j && L->data[i]<=pivot)
			i++;						//从左向右扫描,找一个大于pivot的元素
		if (i<j)
			swap(L->data[i],L->data[j]);//将L->data[i]和L->data[j]进行交换
	}
	swap(L->data[0],L->data[i]);		//将L->data[0]和L->data[i]进行交换
}

解法二（推荐）：

void partition(SqList *&L)
{	int i=0,j=L->length-1;
	ElemType pivot=L->data[0];	//以data[0]为枢轴
	while (i<j)  				//从顺序表两端交替向中间扫描,直至i=j为止
	{	while (j>i && L->data[j]>pivot)
			j--;				//从右向左扫描,找一个小于等于pivot的data[j]
		L->data[i]=L->data[j];	//找到这样的data[j],放入data[i]处
		while (i<j && L->data[i]<=pivot)
			i++;				//从左向右扫描,找一个大于pivot的记录data[i]
		L->data[j]=L->data[i];	//找到这样的data[i],放入data[j]处
	}
	L->data[i]=pivot; //把枢轴元素放到该放的位置
}