浴谷金秋营-基础数据结构（2）

讲师：nzhtl1477

为什么要学数据结构

因为要考

数据结构用来做什么题

维护一些会TLE的题

很强大

并查集

用处

1. 维护一个图，支持动态加边，查询两个点的连通性

---

连通性：是否可以经过若干条边从点a到点b

并查集的连通性是无向的

---

时间复杂度

Q次操作 并查集复杂度可以认为是O(Q)

实现

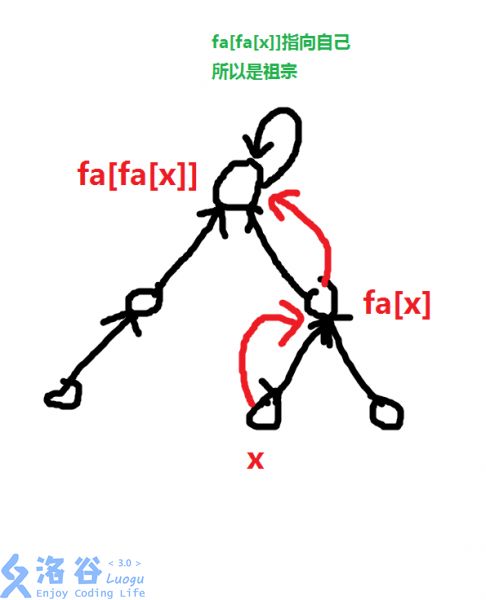
• fa[x]为x节点的父节点

• 若fa[x]为自己本身，则自己就是自己的父亲，也可能就是整个集合的祖先

初始化

因为刚刚开始所有元素都是分离的，即自成一派谁都不是谁的儿子或父亲，所以自己就是自己的祖先，自己就是一个集合。

那么我们就需要初始化为：所有节点的fa都指向自己

int fa[MAXN];
for(int i-1;i<=nli++)fa[i]=i;

查询

若需要查询两个元素a和b是否在用一个集合：找出a的祖先和b的祖先，查看两个元素的祖先是否是同一个。如果祖先一样则说明是处于同一个集合。

inline bool is_A_Set(int x,int y){
    //如果x和y在同一个集合即返回true
    //否则返回false
    int xx=find(x);//find()表示为寻找某个元素的祖宗
    int yy=find(y);
    //xx和yy就分别表示为x的祖宗和y的祖宗
    if(xx==yy)return true;
    else return false;
    //查看祖先是否一致
}

那如何查询祖先呢？对于一个元素x来说，它的父亲是fa[x],他的爷爷是fa[fa[x]]，他的太爷爷是fa[fa[fa[x]]]....则我们可以一直向上查找，直至找到一个没有父亲的节点（fa[x]=x），则说明它就是祖先，因为其无父亲，是整个集合的最高顶点。

inline int find(int x){
    //返回x的祖宗编号
    if(x==fa[x])return x;//如果自己的父亲是自己则说明找到祖先
    else return find(fa[x]);//否则就去寻找父亲的祖先（也就是自己的祖先）
}

还有一种写法

inline int find(int x){
    return x==fa[x] ? x : find(fa[x]);
}

三目运算符 条件？条件成立的值：条件不成立的值

但是以上都是递归型的，其实还有非递归型的

inline int find(int x){
    while(fa[x]!=x)x=fa[x];
    return x;
}

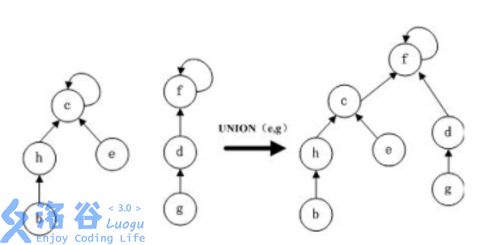
合并——连边

合并两个不相交集合的方法——找到一个集合的父亲的父亲的父亲……的父亲，也就是祖先，将另一个集合的祖先的fa指向它。

inline void merge(int x,int y){
    //合并x和y所在的集合（x和y之间连一条边）
    int xx=find(x);
    int yy=find(y);
    if(xx==yy)return;//如果两个元素本身就处于同一集合，则无需合并
    else{
        fa[yy]=xx;//这里是把yy合并到xx下
        //如果需要把xx合并到yy下（yy做父亲）
        //fa[xx]=yy;
    }    
}

再谈合并

如果单纯的按照上面的思路进行合并会出现问题。

假设有一组精心设计的数据，使你的普通合并如下呈现。

你会惊奇的发现这个集合合并成了一个类似于线性表的结构！！！

若我们需要查询N号元素的祖先，那我们就需要从N找到N-1找到N-2找到...到3到2到祖宗，这样时间复杂度就会非常大！！

1. 按秩合并

2. 路径压缩

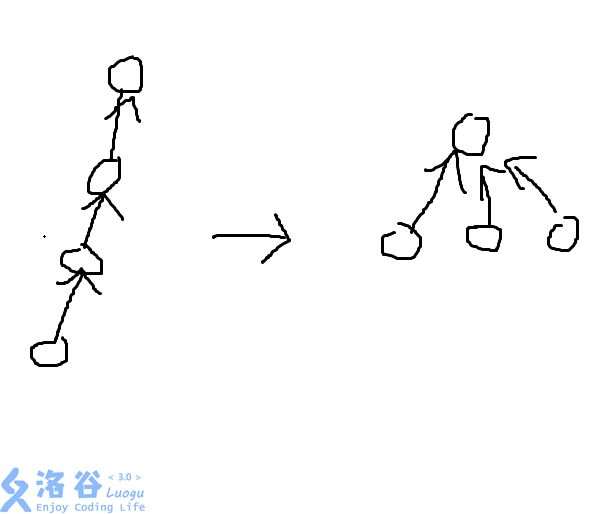
路径压缩

1. 并查集只关心最远的祖先

2. 直接把所有子孙的父亲直接指向祖先

3. 因为寻找祖先是通过递归查找。所以我们可以在回溯时，直接把每层的fa直接指向返回的祖先编号。

这样子我们就可以把所有节点到祖先的路径大大缩短

inline int find(int x){
    if(fa[x]==x)return x;//找到祖先就返回编号
    else return fa[x]=find(fa[x]);
    //这里不仅仅是将递归回溯来的祖先编号返回
    //还顺便把自己的fa指向祖先
    //fa[x]=find(fa[x]);return fa[x];
}

按秩合并

把元素少的集合的祖先，合并到元素多的集合的祖先下。

1. 使得所有节点到祖宗的距离最多+1

2. O(log(N))

例题

1. 洛谷P1197 [JSOI2008]星球大战

2. bzoj2057

3. 洛谷P1525关押罪犯

---

STL

set

本质——一个功能受限的平衡树

头文件

#include

建立一个set

set<类型>集合名；
sets;

加入一个新元素

s.insert(a);

删除元素

s.erase(a);

查找元素

s.find(a);

询问最小值

* s.begin()

询问最大值

* --s.end()

set里有多少个元素

s.size()

清空

s.clear;

遍历

for(set<类型>::iterator i = s.begin();i ！= s.end();i++)

查询某个元素是否存在

if(s.find(1)==s.end())puts(""No);
else puts("Yes");

这里的find()在某个元素不存在时会返回一个类似指针的尾迭代器。

lower_bound

* --s.lower_bound(x);//查询=x的最小元素

以上两个在查询中，若不存在元素满足条件，则会产生不可描述的爆炸

map

本质——功能受限的平衡树

头文件

    #include

建立

maps;
maps;
maps;
maps;

加入一个映射

s[a]=b;

访问映射

s[a]

清空映射

s.clear;

遍历

for(map::iterator i =s.begin();i!=s.end();i++)

priority_queue

[praɪˈɔ:rəti][kju]

本质——二叉堆

翻译——优先队列

头文件

#include

建立

priority_queue<类型>q;

建立大根堆

priority_queueq;

建立小根堆

priority_queue,greater>q;

插入、删除元素

q.push(a);
q.pop();//删除最大（小）值

查询最大值

q.top();

大小

q.size();

例题 洛谷P1090合并果子

---

常数优化

正经的优化

1. inline —— 在无氧环境下有效

2. 倍增表小的开前面，寻址会更快

3. 读入优化

4. 取模优化

5. STL优化

6. 换个写法

玄学的优化

1. 缓存每一级大小不同，速度也不同，所以基数排序时可以通过针对本地机器改动数组大小来获得更快的优化。

2. 如果经常调用a[x],b[x],c[x]这样的数组，放进结构体里会更快。

3. 经常用的东西放进register里（不一定有效）

4. 最大值=50000*50000的时候可以用unsigned代替long long。

5. 常用数组开得越小速度越快

读入优化

fread

struct io{
    char ibuf[1<<25],* s;
    io()
    {
        freopen("in.in","r",stdin);
        fread(s = ibuf,1,1<<25,stdin);
    }
    inline int read(){
        register int u = 0,v = 1;
        while(* s < 48)
              v=* s++ ^ 45 ? 1 : -1;
        while(* s > 32 )
              u = u * 10 + * s++ - 48;
        return u*v;
    }
}ip;

#define read ip.read

mmap

#include
#include
#include
#include

struct io{
    char* s;
    io(){
        s = ( char* ) mmap( NULL , 1<<26 , PROT_READ , fileno( stdin ) , 0);
    }
    inline int read(){
        register int u = 0,v = 1;
        while(* s < 48)
              v=* s++ ^ 45 ? 1 : -1;
        while(* s > 32 )
              u = u * 10 + * s++ - 48;
        return u*v;
    }
}ip;

#define read ip.read

取模优化

#define mod 19260817
inline void update( int & x , int y ){    x += y;
    if( x >= mod ) x -= mod;
  }
update( ans , v );

转载于:https://www.cnblogs.com/Neworld2002/p/8470858.html