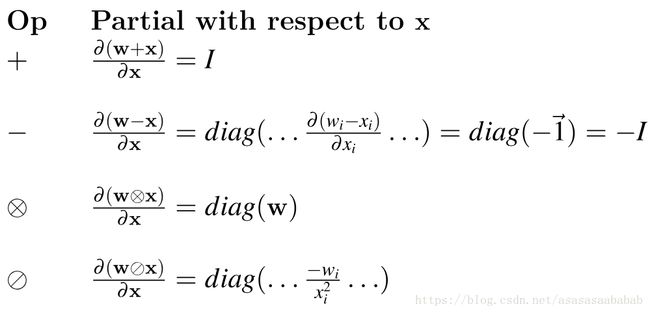深度学习中的Matrix Calculus (1)： Jacobian And Chain Rule

  在深度学习里边，一个最重要的过程是Back Propagation，也就是计算梯度用于做梯度下降优化。然而在BP中，充斥着大量的矩阵微分运算以及各种转化技巧，导致没有学过矩阵论或者矩阵分析的童鞋感到压力山大，所以《深度学习反向求导》这个系列文章主要用最简洁的内容把Matrix Calculus这块的所需内容阐述一遍。

背景：以DNN为例

  DNN，也就是隐含层基本上都是全连接这种神经网络，是一类比较容易分析的神经网络。就以这个为例，阐明我们的目标和任务。

  DNN的各层前向计算如下：

{ZL=WLAL−1+bL,AL=σ(ZL)L=1,…,N. { Z L = W L A L − 1 + b L , A L = σ ( Z L ) L = 1 , … , N .

其中， ZL Z L 是第 L L 层的全连接层（FC）的输出，是一个 nL×1 n L × 1 的向量， AL A L 是第 L L 层的激活层的输出， A0=X A 0 = X 也就是输入， WL W L 是第 L L 层的权重（weights），是一个 nL×nL−1 n L × n L − 1 的矩阵。整个网络的损失函数（loss function）是：

J=J(ZN) J = J ( Z N )

而BP则是需要计算：

⎧⎩⎨⎪⎪∂J∂WL=∂J∂ZN⋅∂ZN∂ZN−1⋅ ⋯ ⋅∂ZL+1∂ZL⋅∂ZL∂WL,∂J∂bL=∂J∂ZN⋅∂ZN∂ZN−1⋅ ⋯ ⋅∂ZL+1∂ZL⋅∂ZL∂bL∀ L=1,2,…,N { ∂ J ∂ W L = ∂ J ∂ Z N ⋅ ∂ Z N ∂ Z N − 1 ⋅   ⋯   ⋅ ∂ Z L + 1 ∂ Z L ⋅ ∂ Z L ∂ W L , ∂ J ∂ b L = ∂ J ∂ Z N ⋅ ∂ Z N ∂ Z N − 1 ⋅   ⋯   ⋅ ∂ Z L + 1 ∂ Z L ⋅ ∂ Z L ∂ b L ∀   L = 1 , 2 , … , N

然后：

∂ZL∂ZL−1=∂ZL∂AL−1⋅∂AL−1∂ZL−1 ∂ Z L ∂ Z L − 1 = ∂ Z L ∂ A L − 1 ⋅ ∂ A L − 1 ∂ Z L − 1

  可见这里边有很多应用链式法则和矩阵求导。所以需要把这块仔细研究好。

  所以本篇加上后续的文章一共三篇，内容分别是基本的Jacobian（向量对向量求导，面向 ∂ZL∂ZL−1 ∂ Z L ∂ Z L − 1 ）这个基本上多元微积分中都学过了，属于回顾；复杂一些的向量和矩阵的函数的求导，主要是迹（trace）的应用(面向 ∂J∂ZN ∂ J ∂ Z N )；对矩阵求导，主要是Kronecker积的应用，面向 ∂ZL∂WL ∂ Z L ∂ W L 。

Vector Calculus

  这个部分其实就是多元微积分的内容，也即 f=f(x,y) f = f ( x , y ) ，那么 f f 的梯度：

▿f=[∂f∂x∂f∂y] ▽ f = [ ∂ f ∂ x ∂ f ∂ y ]

  例如 f=f(x,y)=3x2y f = f ( x , y ) = 3 x 2 y 那么 ▿f=[6xy3x2] ▽ f = [ 6 x y 3 x 2 ] .

Matrix Calculus

  假如我们除了有 f f 这个函数，还有 g g 这个函数，那么我们如果把 f f 和 g g 的梯度按行堆起来，就得到了Jacobian矩阵（雅克比矩阵）：

[▿f▿g]=⎡⎣⎢⎢∂f∂x∂g∂x∂f∂y∂f∂y⎤⎦⎥⎥ [ ▽ f ▽ g ] = [ ∂ f ∂ x ∂ f ∂ y ∂ g ∂ x ∂ f ∂ y ]

  一般的，如果 x x 是一个 n×1 n × 1 的向量：

x=⎡⎣⎢⎢⎢⎢x1x2⋮xn⎤⎦⎥⎥⎥⎥ x = [ x 1 x 2 ⋮ x n ]

   y y 是一个 m×1 m × 1 的向量，每一个元素 yi y i 是 x x 的函数：

y=⎡⎣⎢⎢⎢⎢y1y2⋮yn⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢f1(x)f2(x)⋮fn(x)⎤⎦⎥⎥⎥⎥ y = [ y 1 y 2 ⋮ y n ] = [ f 1 ( x ) f 2 ( x ) ⋮ f n ( x ) ]

  那么对应的Jacobian矩阵是：

∂y∂x=⎡⎣⎢⎢⎢⎢⎢⎢∂f1∂x1∂f2∂x1⋮∂fm∂x1∂f1∂x2∂f2∂x2⋮∂fm∂x2……⋱…∂f1∂xn∂f2∂xn⋮∂fm∂xn⎤⎦⎥⎥⎥⎥⎥⎥ ∂ y ∂ x = [ ∂ f 1 ∂ x 1 ∂ f 1 ∂ x 2 … ∂ f 1 ∂ x n ∂ f 2 ∂ x 1 ∂ f 2 ∂ x 2 … ∂ f 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ f m ∂ x 1 ∂ f m ∂ x 2 … ∂ f m ∂ x n ]

Derivative of Element-Wise Operators

  这个element-wise，也就是针对向量中每一个元素进行运算，例如两个向量求和、求差，逐元素求乘法，逐元素算一个函数等等，这个很简单，直接对着雅克比矩阵的定义就可以计算出来。（下面的例子懒得打公式，就直接贴图了）

  又比如 y=Ax y = A x ，那么 ∂y∂x=A ∂ y ∂ x = A ，那么对于 y=∑ixi y = ∑ i x i ，可以写作 y=1Tx y = 1 T x ，所以梯度也就是 ∂y∂x=1T ∂ y ∂ x = 1 T

  再比如DNN中的 AL=σ(ZL) A L = σ ( Z L ) ，雅克比矩阵就是

∂AL∂ZL=diag(σ′(ZL)) ∂ A L ∂ Z L = d i a g ( σ ′ ( Z L ) )

  这是因为逐元素求函数， aLi=σ(zLi) a i L = σ ( z i L ) ，只和自己对应的那个元素求，所以雅克比矩阵是一个对角阵。

链式法则 Chain Rule

  链式法则本身其实很简单，如果 f:Rm→Rn f : R m → R n , g:Rn→Rk g : R n → R k ，那么：

∂g(f(x))∂x=∂g∂f⋅∂f∂x ∂ g ( f ( x ) ) ∂ x = ∂ g ∂ f ⋅ ∂ f ∂ x

  这个证明用total derivative就可以证了，很简单的（Hint：
f(x+Δx,y+Δy)−f(x,y)=f(x+Δx,y+Δy)−f(x,y+Δy)+f(x,y+Δy)−f(x+Δx,y+Δy) f ( x + Δ x , y + Δ y ) − f ( x , y ) = f ( x + Δ x , y + Δ y ) − f ( x , y + Δ y ) + f ( x , y + Δ y ) − f ( x + Δ x , y + Δ y ) ）。

所以有如下的表达式：

∂ZL∂ZL−1=∂ZL∂AL−1⋅∂AL−1∂ZL−1 ∂ Z L ∂ Z L − 1 = ∂ Z L ∂ A L − 1 ⋅ ∂ A L − 1 ∂ Z L − 1

上边已经计算了：

∂ZL∂AL−1=WL ∂ Z L ∂ A L − 1 = W L

∂AL∂ZL=diag(σ′(ZL)) ∂ A L ∂ Z L = d i a g ( σ ′ ( Z L ) )

所以：

∂ZL∂ZL−1=∂ZL∂AL−1⋅∂AL−1∂ZL−1=WL⋅diag(σ′(ZL)) ∂ Z L ∂ Z L − 1 = ∂ Z L ∂ A L − 1 ⋅ ∂ A L − 1 ∂ Z L − 1 = W L ⋅ d i a g ( σ ′ ( Z L ) )

这样就得到了一个BP中一个重要的结果。