【机器学习与算法】python手写算法：Kmeans和Kmeans++算法

背景

K-Means算法因其算法简单，收敛快等特点而成为最常用的无监督学习方法之一，K-means算法过程如下：

1. 随机选取K个中心点；
2. 计算每个样本点到K个中心点的距离，离谁最近就归为哪一类；
3. 对于每一分类，计算该分类中所有点的均值作为新的中心点；
4. 重复2-3步知道中心点基本不再变化。

K-means算法的一大缺陷就是它对初值（一开始选取的中心点）比较敏感，初值选不好，聚类效果可能很渣。而K-Means++即是对K-Means算法选取初值的一种优化算法，可以让K-Means聚类效果相对更好，而且收敛更快。K-Means++的算法过程如下：

1. 先随机选取第一个中心点；
2. 在这样一个概率密度分布下，选取下一个中心点：
   $$D(x{)}^2/\Sigma (D(x{)}^2)$$
   其中D(x)是样本点距离已选的最近中心点的距离；
3. 重复第2步直至选出n个初始中心点。

K-means++的核心思想就是把距离转换为概率，选取下一个中心点时，距离已选中心点越远，被选中的概率越大。那为啥不直接选取距离所有已选中心点最远的点呢，算法上不是更简单？不这么做主要是因为这样太容易选到异常离群点，从而影响最终的聚类效果。
更详细的算法描述请参看K-Means++文献。

那给定概率权重的随机采样怎么用python实现呢？主要参考了这篇博客，主要思想就是把每个点的概率权重从头到尾接起来，然后从这个范围内随机采样一个值，看这个值落到哪个点的区间内，代码如下：

import random
def random_weight(weight_data):
    total = sum(weight_data.values())    # 权重求和
    ra = random.uniform(0, total)   # 在0与权重和之前获取一个随机数 

    curr_sum = 0
    for k in weight_data.keys():
        curr_sum += weight_data[k]             # 在遍历中，累加当前权重值
        if ra <= curr_sum:          # 当随机数<=当前权重和时，返回权重key
            return k

我们用这个函数随机采样10000个样本看下分布：

weight_data = {'1': 0.1, '2': 0.4, '3': 0.5}
from collections import Counter
res = []
for i in range(10000):
    res.append(random_weight(weight_data))
    
print(Counter(res))

#OUTPUT：
Counter({'3': 4970, '2': 4077, '1': 953})

1、2、3被选中的次数基本符合1:4:5，符合我们的预期。

K-means算法python代码

import pandas as pd
import numpy as np
import random

class K_Means:
    
    def __init__(self,
                 n_cluster=3,
                 init = 'k-means++',
                 max_iter=300,
                 tol=0.0001):
        
        self.n_cluster = n_cluster #最终要聚成的团簇数，同时也是中心点个数
        self.init = init #初始点选取的方式：随机选取或K-means++
        self.max_iter = max_iter #最大迭代次数
        self.tol = tol #判断迭代结果闭合的标准，两次迭代中心点距离小于tol则停止迭代，和sklearn不同，sklearn用的是所有点到其最近点的距离平方和
        self.center = None #记录最终的中心点
        self.flag = [] #记录训练样本最后的分类标签
        
        
    @property #私有化属性——中心点
    def cluster_centers_(self):
        return self.center   
    
    @property #私有化属性——训练样本分类标签
    def labels_(self):
        return np.array(self.flag)    
    
    @property #私有化属性——迭代的次数
    def n_iter_(self):
        return self.n_iter
        
        
    def _eula_distance(self, x1, x2):
        '''
        计算并返回两个点的欧式距离平方
        '''
        return np.sum((x1-x2)**2)
    
    
    def _random_weighted(self, weight_data):
        '''
        weight_data：字典的形式存储每个点及其概率权重
        根据每个点的概率权重，随机采样一个点并返回
        '''

        total = sum(weight_data.values())    # 权重求和
        ra = random.uniform(0, total)   # 在0与权重和之前获取一个随机数 

        curr_sum = 0
        for k in weight_data.keys():
            curr_sum += weight_data[k]             # 在遍历中，累加当前权重值
            if ra <= curr_sum:          # 当随机数<=当前权重和时，返回权重key
                return k
    
    
    def _get_min_eula_dis(self, x, li):
        '''
        计算并返回x和数组li中所有点的最小距离平方，及对应下标
        '''
        res = []
        for item in li:
            res.append(self._eula_distance(x,item))
            
        return min(res), res.index(min(res))
    
    
    def _k_means_plus_plus(self,X):
        '''
        k-means++方法采样n个初始样本点
        '''
        
        #初始化每个样本点被选为中心点的概率权重都为1，及uniformly选第一个中心点
        weight = [1]*X.shape[0]
        point = []
        for i in range(self.n_cluster):
            #生成所有样本点及其概率权重的字典
            weighted_point = {tuple(x):y for x,y in zip(X.values,weight)}
            #根据每个样本的概率权重随机选一个样本作为中心点
            point.append(self._random_weighted(weighted_point))
            #根据已选中的中心点，计算其它样本到已选中心点的最小距离平方，作为新的概率权重
            weight = list(map(lambda x:self._get_min_eula_dis(x,point)[0],X.values))
            
        return np.array(point)
            

    def fit(self, X:pd.DataFrame):
        '''
        K-means训练拟合
        '''

        if self.init ==  'random':
            #随机选n个点做中心点
            self.center = X.sample(self.n_cluster,random_state = 1).values
        elif self.init == 'k-means++':
            #使用k-means++方法选取中心点
            self.center = self._k_means_plus_plus(X)
        else:
            raise KeyError('Only random or k-means++ is allowed!')
        
        iter_num = 1
        while iter_num<self.max_iter:
            #对于训练集中的每个点：把距离最近的中心点的下标返回作为该点的类别标签
            self.flag = list(map(lambda x:self._get_min_eula_dis(x,self.center)[1],X.values))

            new_center = []
            delta = []
            #对于每一类
            for i in set(self.flag):
                #计算该类中所有点的均值
                new_center.append(X.loc[np.where(np.array(self.flag)==i)].mean(axis=0).values)
                #计算两次迭代中心点的距离
                delta.append(self._eula_distance(self.center[i],new_center[i]))
            #把每类的均值点作为新中心点
            self.center = np.array(new_center)
            
            #如果每个中心点和上次迭代的距离都小于tol阈值，则停止迭代
            if np.array(list(map(lambda x:x<self.tol, delta))).all():
                break
                
            iter_num += 1
        
        #记录下迭代的次数
        self.__setattr__('n_iter',iter_num-1)

    
    def predict(self, X):
        '''
        计算距离最近的中心点的下标作为类别标签
        '''

        label = []
        for p in X.values:
            label.append(self._get_min_eula_dis(p, self.center)[1])
            
        return np.array(label)

结果对比

我们把自己实现的K-means算法用随机采样和K-Means++采样分别跑一下结果，并和sklearn结果做一个对比：

if __name__ == '__main__':
    import matplotlib.pyplot as plt
    from sklearn.datasets import make_blobs
    from sklearn.cluster import MiniBatchKMeans, KMeans
    np.random.seed(0)


    #定三个中心点，随机生成800个服从各项同性高斯分布的二维点
    centers = [[1, 1], [-1, -1], [1, -1]]
    n_clusters = len(centers)
    X, labels_true = make_blobs(n_samples=800, centers=centers, cluster_std=0.7)

    #随机采样中心点进行K-means聚类
    km_r = K_Means(init='random')
    km_r.fit(pd.DataFrame(X))

    #k-means++采样中心点进行K-means聚类
    km_pp = K_Means(init='k-means++')
    km_pp.fit(pd.DataFrame(X))

    #调用sklearn包的K-means方法进行对比
    k_means = KMeans(init='k-means++', n_clusters=3, n_init=1)
    k_means.fit(X)

    fig = plt.figure(figsize=(16, 5))
    colors = ['#4EACC5', '#FF9C34', '#4E9A06']

    ax = fig.add_subplot(1, 3, 1)
    for k, col in zip(range(n_clusters), colors):
        my_members = k_means.labels_ == k
        cluster_center = k_means.cluster_centers_[k]
        ax.plot(X[my_members, 0], X[my_members, 1], 'w',
                markerfacecolor=col, marker='.', markersize=9)
        ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
                markeredgecolor='k', markersize=6)
    ax.set_title('KMeans-sklearn')

    ax = fig.add_subplot(1, 3, 2)
    for k, col in zip(range(n_clusters), colors):
        my_members = km_r.labels_ == k
        cluster_center = km_r.cluster_centers_[k]
        ax.plot(X[my_members, 0], X[my_members, 1], 'w',
                markerfacecolor=col, marker='.', markersize=9)
        ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
                markeredgecolor='k', markersize=6)
    ax.set_title('K_Means-python-random')
    plt.text(-3, 1.8,  'iter_nums: %d' % (km_r.n_iter_))

    ax = fig.add_subplot(1, 3, 3)
    for k, col in zip(range(n_clusters), colors):
        my_members = km_pp.labels_ == k
        cluster_center = km_pp.cluster_centers_[k]
        ax.plot(X[my_members, 0], X[my_members, 1], 'w',
                markerfacecolor=col, marker='.', markersize=9)
        ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
                markeredgecolor='k', markersize=6)
    ax.set_title('K_Means-python-k-means++')
    plt.text(-3, 1.8,  'iter_nums: %d' % (km_pp.n_iter_))
    plt.show()

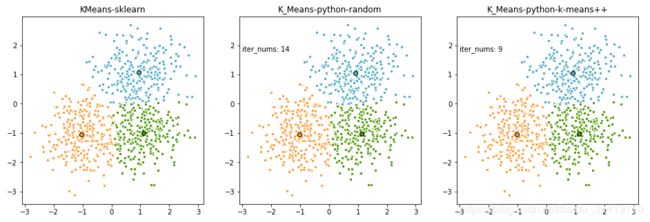
可以看到两种方法和调用sklearn包跑出的结果基本一致，而且使用K-means++选取初始点后，达到收敛的迭代次数明显比随机采样要少。

---

最后，欢迎阅读其它算法的python实现：
【机器学习与算法】python手写算法：Cart树
【机器学习与算法】python手写算法：带正则化的逻辑回归
【机器学习与算法】python手写算法：xgboost算法
【机器学习与算法】python手写算法：Kmeans和Kmeans++算法
【机器学习与算法】python手写算法：softmax回归