3. 运算电路基础
3.1 数字逻辑电路基础
1. 布尔代数
- 0和1分别代表逻辑值“假”和“真”
- 最基本的逻辑运算有：
| 与（AND） | 或（OR） | 非（NOT） |
|---|---|---|
| “ • ” ( “ ∧” ) | “ + ” ( “ ∨ ” ) | “ ¯ ” ( “ ﹁ ” ) |
任何一种逻辑表达式都可写成 这三种基本运算的逻辑组合
例如，异或（XOR）运算的 逻辑表达式为： A ⊕ B = A • B ‾ + A ‾ • B A⊕B=A• \overline B+\overline A•B A⊕B=A•B+A•B,异或运算也称不等价运算。
2. 门电路
（1）一位逻辑门电路
- 三种基本门电路：与门、或门、非门
- 其他门电路可以由三种基本门电路组合形成（如异或门电路）
（2）n位逻辑门电路
（3）组合逻辑部件
- 根据电路是否具有存储功能，将逻辑电路划分为两种类型
–组合逻辑电路：没有存储功能，其输出仅依赖于当前输入
–时序逻辑电路：具有存储功能，其输出不仅依赖于当前输入 ，还依赖于存储单元的当前状态 - 可以利用基本逻辑门电路构成一些具有特定功能的组合逻辑部件 （功能部件）
–如译码器、编码器、多路选择器、加法器等 - 实现一个功能部件的过程 （逻辑函数的化简）
①用一个真值表描述功能部件的输入和输出之间的关系
②根据真值表确定逻辑表达式
③根据逻辑表达式实现逻辑电路
3. 组合逻辑部件
（1）多路选择器
最简单的多路选择器（MUX）是二路选择器
– 有两个输入端A和B，一个输出端F，并有一个控制端S，
– 其功能是 ：当S为0时，F=A；当S为1时，F=B。
k路选择器应有k路输入，因而控制端S的位数应是「log2k」
– 例如，三路或4路选择器，S有两位；5~8路选择器，S有3位。
（2）一位加法器（全加器）
一位加法器称为全加器
– 两个加数为A和B
– 低位进位为Cin
– 和为F
– 向高位的进位为Cout
化简后，逻辑表达式如下:
F = A ⊕ B ⊕ C i n C o u t = A • B + A • C i n + B • C i n F=A⊕B⊕Cin\\Cout=A •B+A •Cin+B •Cin F=A⊕B⊕CinCout=A•B+A•Cin+B•Cin
（3）n位加法器
- n位加法器可用n个全加器实现
加法由逻辑部件实现，而其他所有算术运算部件都基于加法器 和逻辑运算实现，因此，所有算术运算是基于0和1以及逻辑运算实现的！
（4）n位带标志加法器
- n位加法器无法用于两个n位带符号整数 （补码）相加，无法判断是否溢出
- 程序中经常需要比较大小，通过（在加法器中）做减法得到的标志信息来判断
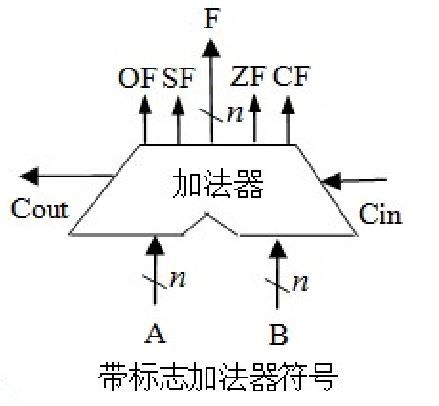
溢 出 标 志 O F ： O F = C n ⊕ C n − 1 符 号 标 志 S F ： S F = F n − 1 零 标 志 Z F : Z F = 1 当 且 仅 当 F = 0 ； 进 位 / 借 位 标 志 C F ： C F = C o u t ⊕ C i n 溢出标志OF： OF=Cn⊕Cn-1 \\ 符号标志SF： SF=Fn-1 \\ 零标志ZF: ZF=1当且仅 当F=0；\\ 进位/借位标志CF： CF=Cout⊕Cin 溢出标志OF：OF=Cn⊕Cn−1符号标志SF：SF=Fn−1零标志ZF:ZF=1当且仅当F=0；进位/借位标志CF：CF=Cout⊕Cin
（5）n位整数加/减运算器
- 利用带标志加法器，可构造整数加/减运算器，进行以下运算：
- 无符号整数加、减
- 带符号整数加、减
在整数加/减运算部件 基础上，加上寄存器、 移位器以及控制逻辑， 就可实现ALU、乘/除运算以及浮点运算电路
（6）算术逻辑部件（ALU）
- 进行基本算术运算与逻辑运算 – 无符号整数加、减
– 带符号整数加、减
– 与、或、非、异或等逻辑运算 - 核心电路是带标志加法器
- 输出除和/差等，还有标志信息
- 有一个操作控制端（ALUop）， 用来决定ALU所执行的处理功能。 ALUop的位数k决定了操作的种类 ，例如，当位数k为3时，ALU最 多只有23=8种操作。
3.2 从C表达式到逻辑电路
以赋值语句 y=(x>>2)+k 为例
1. 从C表达式到运算类指令
C语言程序中的基本数据类型、基本运算类型
（1）基本数据类型
①无符号数(二进制位串)、带符号整数(补码)
②浮点数(IEEE 754标准）
③位串、字符（串）（ASCII码）
（2）基本运算类型
①算术(+ -* / % > < >= <= == !=)
②按位( | & ~ ^)
③逻辑( || && ！)
④移位( << >>）
⑤扩展和截断
2. 从运算类指令到运算电路
（1）将各类表达式编译（转换）为指令序列
例如：y=(x>>2)+k 转换为以下指令序列：
sarw $2, %ax ; x>>2
addw %bx, %ax ; (x>>2) + k
（2）计算机直接执行指令来完成运算
控制器对指令进行译码，产生控制信号送运算电路
（3）操作数在运算电路中运算
sarw $2, %ax：将操作数“2”和“R[ax]”送移位器运算
ddw %bx, %ax：将R[ax]和R[bx]送整数加减器中运算
移位器和整数加减运算器都是由逻辑门电路构成的！
3. 数据的运算
（1）高级语言程序中涉及的运算（以C语言为例）
– 整数算术运算、浮点数算术运算
– 按位、逻辑、移位、位扩展和位截断等运算
（2）指令集中涉及到的运算
– 涉及到的定点数运算
•算术运算
带符号整数：取负/ 符号扩展/ 加/ 减/ 乘/ 除 / 算术移位
无符号整数：0扩展/ 加/ 减/ 乘/ 除/ 逻辑左移/ 逻辑右移
•逻辑运算
逻辑操作：与/ 或/ 非/ …
– 涉及到的浮点数运算：加、减、乘、除
（3）指令中的运算操作在运算电路中进行
– 基本运算部件ALU、通用寄存器组，以及其他部件
3.3 C语言中的各类运算
1. C语言程序中涉及的运算
（1）算术运算（最基本的运算）
- 无符号数、带符号整数、浮点数的+、-、*、/ 、%运算等
（2）按位运算
–用途
• 对位串实现“掩码”（mask）操作或相应的其他处理 （主要用于对多媒体数据或状态/控制信息进行处理）
–操作
• 按位或：“|”
• 按位与：“&”
• 按位取反：“~”
• 按位异或：“^”
Q:如何从数据y中提取低位字节，并使高字节为0？
A:可用“&”实现“掩码”操作：y & 0x00FF
例如，当y=0x0B2C时，得到结果为：0x002C
（3）移位运算
–用途
• 提取部分信息
• 扩大或缩小2、4、8…倍
–操作
• 左移:：x<
从运算符无法区分逻辑移位还是算术移位，由x的类型确定
- 若x为无符号数：逻辑左（右）移
高（低）位移出，低（高）位补0，可能溢出！
Q: 何时可能发生溢出？如何判断溢出？
A: 若高位移出的是1，则左移时发生溢出- 若x为带符号整数：算术左移、算术右移
左移：高位移出，低位补0。可能溢出！
溢出判断： 若移出的位不等于新的符号位，则溢出。
右移：低位移出，高位补符，可能发生有效数据丢失。
- 移位运算和按位运算举例
Q: 对于一个 n （ n ≥8）位的变量 x ，请根据C语言中按位运算的定义， 写出满足下列要求的C语言表达式。
（1） x 的最高有效字节不变，其余各位全变为0。
（2） x 的最低有效字节不变，其余各位全变为0。
（3） x 的最低有效字节全变为0，其余各位取反。
（4） x 的最低有效字节全变1，其余各位不变。
A：
（1）(x>>(n-8))<<(n-8)
（2）x & 0xFF
（3）((x^ ~0xFF) >>8 )<< 8
（4）x | 0xFF
（4）逻辑运算
–用途
• 用于关系表达式的运算
例如，if （x>y andi<100）then ……中的“and”运算
–操作
• “‖”表示“OR”运算
• “&&”表示“AND”运算 例如，if ((x>y) &&(i<100)) then ……
• “!”表示“NOT”运算
–与按位运算的差别
• 符号表示不同：& ~ && ；| ~ ‖；……
• 运算过程不同：按位~ 整体
• 结果类型不同：位串~ 逻辑值
（5）位扩展和位截断运算
–用途
• 类型转换时可能需要数据扩展或截断
–操作
• 没有专门操作运算符，根据类型转换前、后数据长短确定是扩展还是截断
• 扩展：短转长
无符号数：0扩展（前面补0）
带符号整数：符号扩展（前面补符）
• 截断：长转短，强行将高位丢弃，故可能发生“溢出”
例1（扩展操作）： 在大端机上输出si, usi, i, ui的十进制和十六进制值是什么？
short si = -32768;
unsigned short usi = si;
int i = si;
unsingned ui = usi ;
A:
si = -32768 8000 H
usi = 32768 8000H
i = -32768 FFFF 8000H带符号整数：符号扩展
ui = 32768 0000 8000H无符号整数：0扩展
例2（截断操作）：i 和j 是否相等？
int i = 32768;
short si = (short) i;
int j = si;
A:
不相等！
i = 32768 0000 8000 H
si = -32768 8000H
j = -32768 FFFF 8000H
原因：对i截断时发生了“溢出”，即：32768截断为16位数时， 因其超出16位能表示的最大值，故无法截断为正确的16位数！
3.4 整数加减运算
1. 整数加、减运算
- C语言程序中的整数有
–带符号整数，如char、short、int、long型等
–无符号整数，如unsigned char、unsigned short、 unsigned等 - 指针、地址等通常被说明为无符号整数，因而在进行指针或地址运算时，需要进行无符号整数的加、减运算
- 无符号整数和带符号整数的加、减运算电路完全一样，这个运算电路称为整数加减运算部件，基于带标志加法器实现
- 计算机中的加法器，因为只有n位，所以是一种模2n运算系统
2. 整数加减运算部件
（1）补码加减运算要点和运算部件
- 加、减法运算统一采用加法来处理
- 符号位(最高有效位MSB)和数值位一起参与运算
- 直接用Adder实现两个数的加运算（模运算系统）
运算结果高位丢弃，保留低n位，相当于取模2n - 实现减法的主要工作在于：求[–B] 补 , [ – B ] 补 = B ‾ + 1 [–B] 补=\overline B+1 [–B]补=B+1
（2）所有运算电路的核心——加法器
计算机中所有运算都基于加法器实现加法器不知道所运算的是带符号数还是无符号数。加法器不判定对错，总是取低n位作为结果，并生成标志信息。
①零标志ZF、溢出标志OF、进/借位标志CF、符号标志SF称为条件标志
| 标志 | 计算 |
|---|---|
| OF | （带符号数运算）若A与B’同号但与Sum不同号，则1；否则0 |
| SF | sum符号 |
| ZF | 如Sum为0，则1，否则0。 |
| CF | Cout ⊕ sub |
②存放标志的寄存器通常称为程序/状态字寄存器或标志寄存器。每个标志对应标志寄存器中的一个标志位。 如，IA-32中的EFLAGS寄存器。
③生成并保存的条件标志，在分支指令（条件转移指令）中被用作是否转移执行的条件
3. 整数加法举例
4. 整数减法举例
5. 溢出判断
| 无符号 | 带符号 | |
|---|---|---|
| 加溢出 | 进位CF = 1 | OF = 1 |
| 减溢出 | 差为负数，即借位CF = 1 | (1) 最高位和次高位的进位不同 Cn⊕Cn-1 (2) 和的符号位和加数的符号位不同 |
（1）无符号整数加法溢出判断程序
发生溢出时，一定满足 r e s u l t < x result<x result<x and r e s u l t < y result<y result<y
否则，若 x + y − 2 n ≥ x x+y-2^n≥x x+y−2n≥x，则 y ≥ 2 n y≥2^n y≥2n ，这是不可能的
/* Determine whether arguments can be added without overflow */
int uadd_ok(unsigned x, unsigned y)
{
unsigned sum = x+y;
return sum >= x;
}
（2）带符号整数加法溢出判断程序
当两个加数异号，和不会出现溢出；
当两个加数同号，且和与加数符号相反时，出现溢出。
/* Determine whether arguments can be added without overflow */
int tadd_ok(int x, int y)
{
int sum = x+y;
int neg_over = x < 0 && y < 0 && sum >= 0; //负溢出
int pos_over = x >= 0 && y >= 0 && sum < 0; //正溢出
return !neg_over && !pos_over;
}
（3）带符号整数减法溢出判断程序
如果直接调用上面的 tadd_ok(x, -y)，当x=0，y=0x80000000时，会出现函数判断错误。