立体视觉 之 刚体变换

1  投影空间

　欧氏空间，主要描述角度和形状，针对的是理想几何物体。例如，两条 ∥ 线永不相交，或交于无穷远点 (虚拟的点)。中学时代的 “平面与立体几何”，便属于欧式空间。

　投影空间，指实际的物体，被相机拍摄后，成像所在的空间，常用于计算机视觉中。在投影空间里，两条直线必然会相交于一点，只不过当这两条线平行时，交点为无穷远。

　　

　如图所示，现实中的两条铁轨，成像在投影空间时，相交于某一点，也即无穷远点；但在欧氏空间中，无穷远点是理想点，并没有实际意义。

　这样，就需要一种新的表示方法 -- 齐次坐标，将欧氏空间的无穷远点，与投影空间中有实际意义的点，建立起映射关系。

 

 2  齐次坐标

　在平面几何里，采用笛卡尔坐标，则一个点可表示为 $(x, y)^{T}$。如果增加一个坐标值，表示为 $(x, y, 1)^{T}$，且约定 ($x, y, 1)^{T}$ 和 $(kx, ky, k)^{T}$ 表示的是同一个点 (其中 k ≠ 0)，

则这种用一个 N+1 维的向量，来表示 N 维向量的方法，称为齐次坐标法。

　这样，由齐次坐标 $(x, y, w)$，可推导出笛卡尔坐标 $ (\dfrac{x}{w}, \dfrac{y}{w})$

2.1  无穷远点

    欧式空间中，两条平行线方程组，如下：

　$\begin{cases} AX + BY + C = 0 \\ AX + BY + D = 0 \end{cases} $ ，其中 C ≠ D

　齐次坐标点$(x, y, w)^{T}$ 与 欧氏空间点 $(X, Y)^{T}$ 的对应关系为： $ X = \dfrac{x}{w}, Y = \dfrac{y}{w}$，代入上面方程组得：

　$\begin{cases} A\dfrac{x}{w} + B\dfrac{y}{w} + C = 0 \\ A\dfrac{x}{w} + B\dfrac{y}{w} + D = 0 \end{cases} $  =>  $\begin{cases} Ax+ By + Cw = 0 \\ Ax+ By + Dw = 0 \end{cases} $ => $w = 0$

　既然 w = 0，则齐次坐标为 $(x, y, 0)^{T}$，对应笛卡尔坐标 $(\dfrac{x}{0}, \dfrac{y}{0})^{T}$，表示的是无穷远点 $(∞, ∞)^{T}$

2.2  合并加法

　点 $(x, y, z)^{T}$，经过伸缩和平移后，成为点 $ (x', y', z')^{T} = (r_{1}x+t_{1}, r_{2}y+t_{2}, r_{3}z+t_{3})^{T}$，该变换过程可用如下公式表示：

　$\begin{bmatrix} x' \\ y' \\ z' \end{bmatrix} = \begin{bmatrix} r_{1} \\ r_{2} \\ r_{3}  \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} + \begin{bmatrix} t_{1} \\ t_{2} \\ t_{3} \end{bmatrix} $

　如果使用齐次坐标，则可将平移变换，转化为矩阵乘法，消除了上式中的矩阵加法

　$\begin{bmatrix} x' \\ y' \\ z' \\1 \end{bmatrix} = \begin{bmatrix} r_{1} & 0 & 0 & t_{1} \\ 0 & r_{2} & 0 & t_{2} \\ 0 & 0 & r_{3} & t_{3} \\ 0 & 0 & 0 & 1  \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1\end{bmatrix} $

2.3 向量和点

    齐次坐标还可以区分向量和点，具体如何区分的，尚待研究 ... ...

 

3  刚体变换

3.1  刚体定义

　欧氏空间中，当物体被视为刚体时，不管是该物体的位置或朝向发生变化，还是更换观察的坐标系，其大小和形状都保持不变。

    形象点说，猪八戒的九齿钉耙，由冰铁铸造而成，便是一种刚体；而镇元子大仙的七星鞭，由于是龙皮做的，故为非刚体。

3.2  位置和朝向

　所谓刚体变换，就是一个可被看做刚体的物体，从一个状态 (位置和朝向)，转换为另一个状态的过程。

   

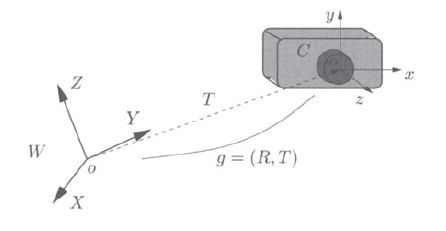
　如上所示，从世界坐标系到相机坐标系的转换，朝向由旋转矩阵 $R$ 表示，位置则由平移矩阵 $T$ 来表示： $ P_{c} = R \cdot P_{w} + T$

　其中，旋转矩阵 $  R = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} $，平移矩阵 $  T = \begin{bmatrix} t_{1} \\ t_{2} \\ t_{3}   \end{bmatrix} $

　旋转矩阵 R 为正交矩阵 (也即，RR' = E，E 为单位矩阵)，则满足以下 6 个约束条件

　(1)  大小约束   $\begin{cases} r_{11}^2 + r_{12}^2 + r_{13}^2 = 1 \\ r_{21}^2 + r_{22}^2 + r_{23}^2 = 1 \\ r_{31}^2 + r_{32}^2 + r_{33}^2 = 1\end{cases} $        (2) 方向约束   $\begin{cases} r_{11}*r_{21} + r_{12}*r_{22} + r_{13}*r_{23} = 0 \\ r_{21}*r_{31} + r_{22}*r_{32} + r_{23}*r_{33} = 0 \\ r_{31}*r_{11} + r_{32}*r_{12} + r_{33}*r_{13} = 0\end{cases} $

   可用一个最简单的正交矩阵 E，来理解上面的约束条件

       $\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$

3.3  转换关系

    若已知 $R$ 和 $T$，则可将世界坐标系内的空间点，与相机坐标系内的空间点，建立起一一对应的关系

　$ \begin{bmatrix} X_{c} \\ Y_{c} \\ Z_{c} \end{bmatrix} = \begin{bmatrix} R & T \end{bmatrix} \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \end{bmatrix}$

3.3.1  约束分析

    $R$ 和 $T$ 共有 12 个未知量，减去正交约束的 6 个方程，则还剩 6 个未知量。

    表面上看，似乎只需 2 组共轭点，就可得到 6 个约束方程，对应求出剩余的 6 个未知量。实际上，这 6 个方程是有冗余信息的 (两组共轭点，在各自的坐标系下，两点之间的距离相等)

    因此，第 2 组共轭点，只是提供了 2 个约束方程，加上第 1 组共轭点的 3 个约束，共有 5 个独立的约束方程。

    显然，还需要第 3 组共轭点，提供 1 个独立的方程，才能求得 $R$ 和 $T$

3.3.2  几何解释

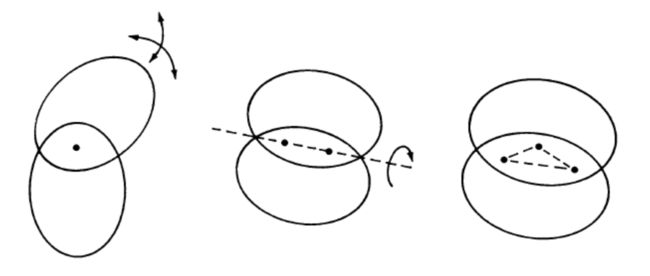
    如下图所示，考虑两个刚体，它们之间存在着相互 旋转 和 平移

   

   首先，在每个刚体上，各选一个点 L1 和 R1，移动其中一个刚体，使得这两个点重合。此时，一个刚体可相对于另一个刚体转动 (以三种不同的方式)。

   然后，在每个刚体上，再分别取一个点 L2 和 R2，并且 | L2 - L1 | = | R2 - R1 |，移动一个刚体，使得这两对点，分别重合。此时，一个刚体可以相对另一个转动 (以一种方式)。

   最后，在每个刚体上，分别取第三个点 L3 和 R3，满足 | L3 - L1 | = | R3 - R1 | 且 | L3 - L2 | = | R3 - R2 |，然后将这三个点对齐。此时，两个刚体便牢牢的连在了一起。

 

 参考资料

    <视觉测量> 张广军，第2章

    Chapter 13

    Chapter 2

    Homogeneous Coordinates