MonoGRNet: A Geometric Reasoning Network for Monocular 3D Object Localization

MonoGRNet: A Geometric Reasoning Network for Monocular 3D Object Localization

MonoGRNet：单张图像估测物体三维位置

Zengyi Qin, Jinglu Wang, Yan Lu

Tsinghua University
Microsoft Research

geometric [,dʒɪə'metrɪk]：adj. 几何学的，几何学图形的
reason ['riːz(ə)n]：n. 理由，理性，动机 vi. 推论，劝说 vt. 说服，推论，辩论
monocular [mə'nɒkjʊlə]：adj. 单眼的，单眼用的
localization [,ləʊkəlaɪ'zeɪʃən]：n. 定位，局限，地方化
Tsinghua University：清华大学，清华
Microsoft Research Asia，MSRA：微软亚洲研究院
the Association for the Advancement of Artificial Intelligence，the American Association for Artificial Intelligence，AAAI：美国人工智能协会
Computer Science，CS：计算机科学
Computer Vision，CV：计算机视觉
peer [pɪə]：n. 贵族，同等的人，同龄人 vi. 凝视，盯着看，窥视 vt. 封为贵族，与...同等

arXiv (archive - the X represents the Greek letter chi [χ]) is a repository of electronic preprints approved for posting after moderation, but not full peer review.

The work was done when Zengyi Qin was an intern at MSR. Copyright © 2019, Association for the Advancement of Artificial Intelligence (www.aaai.org). All rights reserved.

Abstract

Localizing objects in the real 3D space, which plays a crucial role in scene understanding, is particularly challenging given only a single RGB image due to the geometric information loss during imagery projection. We propose MonoGRNet for the amodal 3D object localization from a monocular RGB image via geometric reasoning in both the observed 2D projection and the unobserved depth dimension. MonoGRNet is a single, unified network composed of four task-specific subnetworks, responsible for 2D object detection, instance depth estimation (IDE), 3D localization and local corner regression. Unlike the pixel-level depth estimation that needs per-pixel annotations, we propose a novel IDE method that directly predicts the depth of the targeting 3D bounding box’s center using sparse supervision. The 3D localization is further achieved by estimating the position in the horizontal and vertical dimensions. Finally, MonoGRNet is jointly learned by optimizing the locations and poses of the 3D bounding boxes in the global context. We demonstrate that MonoGRNet achieves state-of-the-art performance on challenging datasets.
由于在图像投影期间几何信息丢失，仅在单个 RGB 图像上定位实际 3D 空间中的目标 (其在场景理解中起关键作用) 是特别具有挑战性的。我们通过观察到的 2D 投影和未观察到的深度维度经由几何推理，针对单眼 RGB 图像提出 MonoGRNet 用于amodal 3D 目标定位。MonoGRNet 是一个单一的统一网络，由四个任务特定的子网络组成，负责 2D 目标检测，实例深度估计 (IDE)，3D 定位和局部角落回归。与需要逐像素标注的像素级深度估计不同，我们提出了一种新的 IDE 方法，该方法使用稀疏监督直接预测目标 3D 边界框中心的深度。通过估计水平和垂直维度中的位置来进一步实现 3D 定位。最后，通过优化全局环境中 3D 边界框的位置和姿势，共同学习 MonoGRNet。我们证明 MonoGRNet 在具有挑战性的数据集上实现了最先进的性能。

projection [prə'dʒekʃ(ə)n]：n. 投射，规划，突出，发射，推测
crucial ['kruːʃ(ə)l]：adj. 重要的，决定性的，定局的，决断的
unobserved [ʌnəb'zɜːvd]：adj. 未被遵守的，未被注意的
supervision [,suːpə'vɪʒn; ,sjuː-]：n. 监督，管理

在图像中，传统的物体定位或检测估计二维边界框，可以框住图像平面上属于物体的可见部分。但是，这种检测结果无法在真实的 3D 世界中提供场景理解的几何感知，对很多应用的意义并不大。

MonoGRNet 从单目 RGB 图像中通过几何推断，在已观察到的二维投影平面和在未观察到的深度维度中定位物体非模态三维边界框 (amodal 3D bounding box，ABBox-3D)，实现了由二维图像确定物体的三维位置。

Amodal perception is the perception of the whole of a physical structure when only parts of it affect the sensory receptors. (当只有部分物理结构影响感觉受体时，Amodal 感知是对整个物理结构的感知。)

Introduction

Typical object localization or detection from a RGB image estimates 2D boxes that bound visible parts of the objects belonging to the specific classes on the image plane. However, this kind of result cannot provide geometric perception in the real 3D world for scene understanding, which is crucial for applications, such as robotics, mixed reality, and autonomous driving.
在 RGB 图像中，传统的物体定位或检测估计二维边界框，可以框住图像平面上属于特定类的物体的可见部分。但是，这种检测结果无法在真实的 3D 世界中提供场景理解的几何感知，而这对于诸如机器人，混合现实和自动驾驶的应用是至关重要的。

robotic [ro'bɑtɪk]：adj. 机器人的，像机器人的，自动的 n. 机器人学
mixed reality，MR：混合现实
autonomous [ɔː'tɒnəməs]：adj. 自治的，自主的，自发的
perception [pə'sepʃ(ə)n]：n. 认识能力，知觉，感觉，洞察力，看法，获取

In this paper, we address the problem of localizing amodal 3D bounding boxes (ABBox-3D) of objects at their full extents from a monocular RGB image. Unlike 2D analysis on the image plane, 3D localization with the extension to an unobserved dimension, i.e., depth, not solely enlarges the searching space but also introduces inherent ambiguity of 2D-to-3D mapping, increasing the task’s difficulty significantly.
在本文中，我们解决了从单眼 RGB 图像完全定位物体非模态三维边界框 (ABBox-3D) 的问题。与图像平面上的 2D 分析不同，具有未观察到的维度 (深度) 扩展的 3D 定位不仅仅扩大了搜索空间，而且还引入了 2D 到 3D 映射的固有模糊性，显著地增加了任务的难度。

ambiguity [æmbɪ'gjuːɪtɪ]：n. 含糊，不明确，暧昧，模棱两可的话
inherent [ɪn'hɪər(ə)nt; -'her(ə)nt]：adj. 固有的，内在的，与生俱来的，遗传的
enlarge [ɪn'lɑːdʒ; en-]：vi. 扩大，放大，详述 vt. 扩大，使增大，扩展

Most state-of-the-art monocular methods (Xu and Chen 2018; Zhuo et al. 2018) estimate pixel-level depths and then regress 3D bounding boxes. Nevertheless, pixel-level depth estimation does not focus on object localization by design. It aims to minimize the mean error for all pixels to get an average optimal estimation over the whole image, while objects covering small regions are often neglected (Fu et al. 2018), which drastically downgrades the 3D detection accuracy.
大多数最先进的单眼方法 (Xu and Chen 2018; Zhuo et al. 2018) 估计像素级深度，然后回归 3D 边界框。然而，像素级深度估计并不专注物体定位。它旨在最小化所有像素的平均误差，以获得对整个图像的平均最佳估计，而覆盖小区域的物体通常被忽略 (Fu et al. 2018)，这大大降低了 3D 检测精度。

neglect [nɪ'glekt]：vt. 疏忽，忽视，忽略 n. 疏忽，忽视，怠慢
downgrade ['daʊngreɪd; daʊn'greɪd]：n. 退步，下坡 adj. 下坡的 adv. 下坡地
amodal 3D bounding boxes，ABBox-3D：非模态三维边界框
instance depth estimation，IDE：实例深度估计，个体深度估计
instance-level depth estimation，IDE：个体级深度估计
local corner regression：局部角落回归
coarse [kɔːs]：adj. 粗糙的，粗俗的，下等的

We propose MonoGRNet, a unified network for amodal 3D object localization from a monocular image. Our key idea is to decouple the 3D localization problem into several progressive sub-tasks that are solvable using only monocular RGB data. The network starts from perceiving semantics in 2D image planes and then performs geometric reasoning in the 3D space.
我们提出 MonoGRNet (a unified network)，用于从单眼图像中进行 amodal 3D 物体定位。我们的主要思想是将 3D 定位问题解耦为几个可以仅使用单目 RGB 数据解决的渐进子任务。网络从感知 2D 图像平面中的语义开始，然后在 3D 空间中执行几何推理。

MonoGRNet 的主要思想是将 3D 定位问题解耦为几个渐进式子任务，这些子任务可以使用单目 RGB 数据来解决。网络从感知 2D 图像平面中的语义开始，然后在 3D 空间中执行几何推理。

progressive [prə'gresɪv]：adj. 进步的，先进的 n. 改革论者，进步分子
semantic [sɪ'mæntɪk]：adj. 语义的，语义学的 (等于 semantical)
semantics [sɪ'mæntɪks]：n. 语义学，语义论

A challenging problem we overcome is to accurately estimate the depth of an instance’s 3D center without computing pixel-level depth maps. We propose a novel instance-level depth estimation (IDE) module, which explores large receptive fields of deep feature maps to capture coarse instance depths and then combines early features of a higher resolution to refine the IDE.
我们克服的一个具有挑战性的问题是在不计算像素级深度图的情况下准确估计实例 3D 中心的深度。我们提出了一种新颖的实例级深度估计 (IDE) 模块，它探索深度特征图的大型感受野以捕获粗实例深度，然后将更高分辨率的早期特征组合到 IDE 中。

receptive [rɪ'septɪv]：adj. 善于接受的，能容纳的
coarse [kɔːs]：adj. 粗糙的，粗俗的，下等的

这里需要克服一个具有挑战性的问题是，在不计算像素级深度图的情况下准确估计实例 3D 中心的深度。该论文提出了一种新的个体级深度估计 (instance-level depth estimation，IDE) 模块，该模块探索深度特征图的大型感知域以捕获粗略的实例深度，然后联合更高分辨率的早期特征以优化 IDE。

To simultaneously retrieve the horizontal and vertical position, we first predict the 2D projection of the 3D center. In combination with the IDE, we then extrude the projected center into real 3D space to obtain the eventual 3D object location. All the components are integrated into the end-to-end network, MonoGRNet, featuring its three 3D reasoning branches illustrated in Fig. 1, and is finally optimized by a joint geometric loss that minimizes the 3D bounding box discrepancy in the global context.
为了同时检索水平和垂直位置，我们首先预测 3D 中心的 2D 投影。结合 IDE，我们将投影中心拉伸到真实 3D 空间以获得最终的 3D 物体位置。所有组件都集成到端到端网络 MonoGRNet 中，其中包含图 1 所示的三个 3D 推理分支，最终通过联合几何损失进行优化，最大限度地减少了全局环境中的 3D 边界框差异。

simultaneously [,sɪml'teɪnɪəslɪ]：adv. 同时地
extrude [ɪk'struːd; ek-]：vt. 挤出，压出，使突出，逐出 vi. 突出，喷出
eventual [ɪ'ven(t)ʃʊəl]：adj. 最后的，结果的，可能的，终于的
discrepancy [dɪs'krep(ə)nsɪ]：n. 不符，矛盾，相差

为了同时检索水平和垂直位置，首先要预测 3D 中心的 2D 投影。结合 IDE，然后将投影中心拉伸到真实 3D 空间以获得最终的 3D 物体位置。所有组件都集成到端到端网络 MonoGRNet 中，其中有三个 3D 推理分支，Fig. 1 示例。最后通过联合的几何损失函数进行优化，最大限度地减少 3D 边界在整体背景下的边界框的差异。

We argue that RGB information alone can provide almost accurate 3D locations and poses of objects. Experiments on the challenging KITTI dataset demonstrate that our network outperforms the state-of-art monocular method in 3D object localization with the least inference time. In summary, our contributions are three-fold:
我们认为 RGB 信息本身可以提供几乎准确的 3D 位置和物体姿势。对具有挑战性的 KITTI 数据集的实验表明，我们的网络在 3D 物体定位方面优于最先进的单眼方法，且推理时间最短。总之，我们的贡献是三方面的：

• A novel instance-level depth estimation approach that directly predicts central depths of ABBox-3D in the absence of dense depth data, regardless of object occlusion and truncation.
  一种新颖的实例级深度估计方法，不管物体遮挡和截断，即可在没有密集深度数据的情况下直接预测 ABBox-3D 的中心深度。

absence ['æbs(ə)ns]：n. 没有，缺乏，缺席，不注意

• A progressive 3D localization scheme that explores rich feature representations in 2D images and extends geometric reasoning into 3D context.
  渐进式 3D 定位方案，探索 2D 图像中丰富的特征表示，并将几何推理扩展到 3D 上下文中。

• A unified network that coordinates localization of objects in 2D, 2.5D and 3D spaces via a joint optimization, which performs efficient inference (taking ∼0.06s/image).
  一个统一的网络，通过联合优化协调 2D、2.5D 和 3D 空间中物体的定位，执行有效的推理 (执行 ~0.06s /图像)。

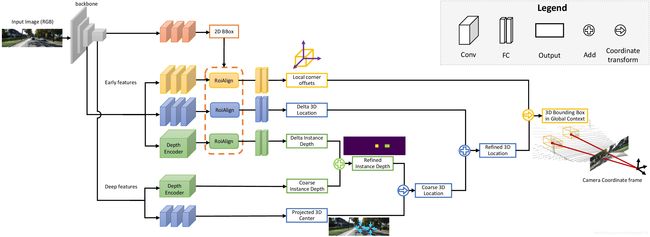
Figure 1: MonoGRNet for 3D object localization from a monocular RGB image. MonoGRNet consists of four subnetworks for 2D detection (brown), instance depth estimation (green), 3D location estimation (blue) and local corner regression (yellow). Guided by the detected 2D bounding box, the network first estimates depth and 2D projection of the 3D box’s center to obtain the global 3D location, and then regresses corner coordinates in local context. The final 3D bounding box is optimized in an end-to-end manner in the global context based on the estimated 3D location and local corners. (Best viewed in color.)
Figure 1：用于从单目 RGB 图像进行 3D 物体定位的 MonoGRNet。MonoGRNet 由四个子网络组成，用于 2D 检测 (棕色)，实例深度估计 (绿色)，3D 位置估计 (蓝色) 和局部角落回归 (黄色)。在检测到的 2D 边界框的引导下，网络首先估计 3D 框中心的深度和 2D 投影以获得全局 3D 位置，然后在本地环境中回归角坐标。最终的 3D 边界框基于估计的 3D 位置和局部角落在全局环境中以端到端的方式进行优化。

Related Work

Our work is related to 3D object detection and monocular depth estimation. We mainly focus on the works of studying 3D detection and depth estimation, while 2D detection is the basis for coherence.
我们的工作涉及 3D 物体检测和单眼深度估计。我们主要关注研究 3D 检测和深度估计的工作，而 2D 检测是连贯性的基础。

coherence [kə(ʊ)'hɪər(ə)ns; kə(ʊ)'hɪərəns]：n. 一致，连贯性，凝聚

2D Object Detection. 2D object detection deep networks are extensively studied. Region proposal based methods (Girshick 2015; Ren et al. 2017) generate impressive results but perform slowly due to complex multi-stage pipelines. Another group of methods (Redmon et al. 2016; Redmon and Farhadi 2017; Liu et al. 2016; Fu et al. 2017) focusing on fast training and inferencing apply a single stage detection. Multi-net (Teichmann et al. 2016) introduces an encoder-decoder architecture for real-time semantic reasoning. Its detection decoder combines the fast regression in Yolo (Redmon et al. 2016) with the size-adjusting RoiAlign of Mask-RCNN (He et al. 2017), achieving a satisfied speed-accuracy ratio. All these methods predict 2D bounding boxes of objects while none 3D geometric features are considered.
2D Object Detection. 二维物体检测深度网络被广泛研究。基于候选区域的方法 (Girshick 2015; Ren et al. 2017) 产生了令人印象深刻的结果，但由于复杂的多阶段管道而表现缓慢。另一组方法 (Redmon et al. 2016; Redmon and Farhadi 2017; Liu et al. 2016; Fu et al. 2017) 侧重于快速训练和推理应用单阶段检测。Multi-net (Teichmann et al. 2016) 引入了用于实时语义推理的编码器 - 解码器架构。它的检测解码器结合了 Yolo (Redmon et al. 2016) 的快速回归和 Mask-RCNN 的尺寸调整 RoiAlign (He et al. 2017)，实现了令人满意的速度准确率。所有这些方法都预测物体的 2D 边界框，而没有考虑任何 3D 几何特征。

3D Object Detection. Existing methods range from single-view RGB (Chen et al. 2016; Xu and Chen 2018; Chabot et al. 2017; Kehl et al. 2017), multi-view RGB (Chen et al. 2017; Chen et al. 2015; Wang et al. ), to RGB-D (Qi et al. 2017; Song and Xiao 2016; Liu et al. 2015; Zhang et al. 2014). While geometric information of the depth dimension is provided, the 3D detection task is much easier. Given RGB-D data, FPointNet (Qi et al. 2017) extrudes 2D region proposals to a 3D viewing frustum and then segments out the point cloud of interest object. MV3D (Chen et al. 2017) generates 3D object proposals from bird’s eye view maps given LIDAR point clouds, and then fuses features in RGB images, LIDAR front views and bird’s eye views to predict 3D boxes. 3DOP (Chen et al. 2015) exploits stereo information and contextual models specific to autonomous driving.
3D Object Detection. 现有的方法从 single-view RGB (Chen et al. 2016; Xu and Chen 2018; Chabot et al. 2017; Kehl et al. 2017), multi-view RGB (Chen et al. 2017; Chen et al. 2015; Wang et al. ), to RGB-D (Qi et al. 2017; Song and Xiao 2016; Liu et al. 2015; Zhang et al. 2014)。提供深度维度的几何信息，3D 检测任务就更加容易了。给定 RGB-D 数据，FPointNet (Qi et al. 2017) 将 2D 候选区域推广到 3D 视锥体，然后分割出感兴趣的点云物体。MV3D (Chen et al. 2017) 根据 LIDAR 点云从鸟瞰图中生成 3D 目标候选区域，然后融合 RGB 图像，LIDAR 前视图和鸟瞰图中的特征来预测 3D 框。3DOP (Chen et al. 2015) 利用立体信息和特定情境模型进行自动驾驶。

Light Detection and Ranging，LiDAR：激光检测与测量，激光雷达
frustum ['frʌstəm]：n. 截头锥体，平截头体 (复数 frustums 或 frusta)

The most related approaches to ours are using a monocular RGB image. Information loss in the depth dimension significantly increases the task’s difficulty. Performances of state-of-the-art such methods still have large margins to RGB-D and multi-view methods. Mono3D (Chen et al. 2016) exploits segmentation and context priors to generate 3D proposals. Extra networks for semantic and instance segmentation are required, which cost more time for both training and inference. Xu et al.(Xu and Chen 2018) leverage a pretrained disparity estimation model (Mahjourian, Wicke, and Angelova 2018) to guide the geometry reasoning. Other methods (Chabot et al. 2017; Kehl et al. 2017) utilize 3D CAD models to generate synthetic data for training, which provides 3D object templates, object poses and their corresponding 2D projections for better supervision. All previous methods exploit additional data and networks to facilitate the 3D perception, while our method only requires annotated 3D bounding boxes and no extra network needs to train. This makes our network much light weighted and efficient for training and inference.
我们最相关的方法是使用单眼 RGB 图像。深度维度中的信息丢失显着增加了任务的难度。最先进方法的性能仍然与 RGB-D 和多视图方法具有很大的差距。Mono3D (Chen et al.2016) 利用分割和上下文先验来生成 3D 候选区域。需要用于语义和实例分割的额外网络，这花费了更多的训练和推理时间。Xu et al.(Xu and Chen 2018) 利用预训练的视差估计模型 (Mahjourian, Wicke, and Angelova 2018) 来指导几何推理。其他方法 (Chabot et al. 2017; Kehl et al. 2017) 利用 3D CAD 模型生成用于训练的合成数据，其提供 3D 物体模板，物体姿势及其相应的 2D 投影以便更好地监督。所有先前的方法利用额外的数据和网络来促进 3D 感知，而我们的方法仅需要带标注的 3D 边界框并且不需要额外的网络训练。这使我们的网络重量轻，有效地进行训练和推理。

Monocular Depth Estimation. Recently, although many pixel-level depth estimation networks (Fu et al. 2018; Eigen and Fergus 2015) have been proposed, they are not sufficient for 3D object localization. When regressing the pixel-level depth, the loss function takes into account every pixel in the depth map and treats them without significant difference. In a common practice, the loss values from each pixel are summed up as a whole to be optimized. Nevertheless, there is a likelihood that the pixels lying in an object are much fewer than those lying in the background, and thus the low average error does not indicate the depth values are accurate in pixels contained in an object. In addition, dense depths are often estimated from disparity maps that may produce large errors at far regions, which may downgrade the 3D localization performance drastically.
单目深度估计。 最近，尽管已经提出了许多像素级深度估计网络 (Fu et al. 2018; Eigen and Fergus 2015)，但它们不足以进行 3D 物体定位。当回归像素级深度时，损失函数考虑深度图中的每个像素并对其进行处理而没有显着差异。在通常的实践中，将每个像素的损失值总计为一个整体以进行优化。然而，存在于物体中的像素可能比位于背景中的像素少得多，因此低平均误差并不表示物体中包含的像素中的深度值是准确的。另外，通常从视差图估计密集深度，该视差图可能在远区域产生大的误差，这可能大大降低 3D 定位性能。

disparity [dɪ'spærɪtɪ]：n. 不同，不一致，不等

Different from the abovementioned pixel-level depth estimation methods, we are the first to propose an instance-level depth estimation network which jointly takes semantic and geometric features into account with sparse supervision data.
与上述像素级深度估计方法不同，我们首先提出了一种实例级深度估计网络，该网络将稀疏监督数据与语义和几何特征结合起来。

Approach

We propose an end-to-end network, MonoGRNet, that directly predicts ABBox-3D from a single RGB image. MonoGRNet is composed of a 2D detection module and three geometric reasoning subnetworks for IDE, 3D localization and ABBox-3D regression. In this section, we first formally define the 3D localization problem and then detail MonoGRNet for four subnetworks.
我们提出了一种端到端网络 MonoGRNet，它可以直接从单个 RGB 图像预测 ABBox-3D。MonoGRNet 由 2D 检测模块和三个几何推理子网组成，用于 IDE，3D 定位和 ABBox-3D 回归。在本节中，我们首先正式定义 3D 定位问题，然后详细介绍 MonoGRNet 的四个子网。

Problem Definition

Given a monocular RGB image, the objective is to localize objects of specific classes in the 3D space. A target object is represented by a class label and an ABBox-3D, which bounds the complete object regardless of occlusion or truncation. An ABBox-3D is defined by a 3D center $\mathbf{C}=(X_c,Y_c,Z_c)$ in global context and eight corners $\mathcal{O}=\{{\mathbf{O}}_k\},k=1,...,8$, related to local context. The 3D location $\mathbf{C}$ is calibrated in the camera coordinate frame and the local corners $\mathcal{O}$ are in a local coordinate frame, shown in Fig. 2 (b) and (c) respectively.
给定单眼 RGB 图像，目标是在 3D 空间中定位特定类的物体。目标物体由类标签和 ABBox-3D 表示，ABBox-3D 无论遮挡还是截断，都会框住整个物体。ABBox-3D 在全局上下文由 3D 中心定义 $\mathbf{C}=(X_c,Y_c,Z_c)$ 和八个角 $\mathcal{O}=\{{\mathbf{O}}_k\},k=1,...,8$，与局部上下文有关。3D 位置 $\mathbf{C}$ 在摄像机坐标系中校准，局部角 $\mathcal{O}$ 位于局部坐标系中，分别如图 Fig. 2 (b) and (c) 所示。

We propose to separate the 3D localization task into four progressive sub-tasks that are resolvable using only a monocular image. First, the 2D box $B_{2d}$ with a center $\mathbf{b}$ and size $(w,h)$ bounding the projection of the ABBox-3D is detected. Then, the 3D center $\mathbf{C}$ is localized by predicting its depth $Z_c$ and 2D projection $\mathbf{c}$. Notations are illustrated in Fig. 2. Finally, local corners $\mathcal{O}$ with respect to the 3D center are regressed based on local features. In summary, we formulate the ABBox-3D localization as estimating the following parameters of each interest object:
我们建议将 3D 定位任务分成四个仅使用单眼图像可解决的渐进子任务。首先，检测到具有中心 $\mathbf{b}$ 和大小 $(w,h)$ 的 2D 框 $B_{2d}$，其框住了 ABBox-3D 的投影。然后，3D 中心 $\mathbf{C}$ 通过预测其深度 $Z_c$ 和 2D 投影 $\mathbf{c}$ 来进行定位。符号如图 2 所示。最后，相对于 3D 中心的局部角 $\mathcal{O}$ 基于局部特征进行回归。总之，我们将 ABBox-3D 定位表示为估计每个感兴趣物体的以下参数：

$$B_{3d}=(B_{2d},Z_c,\mathbf{c},\mathcal{O})\text{\hspace{1em}(1)}$$

Figure 2: Notation for 3D bounding box localization.

Monocular Geometric Reasoning Network

MonoGRNet is designed to estimate four components, $B_{2d},Z_c,\mathbf{c},\mathcal{O}$ with four subnetworks respectively. Following a CNN backbone, they are integrated into a unified framework, as shown in Fig. 1.
MonoGRNet 旨在分别估计四个子组件 $B_{2d},Z_c,\mathbf{c},\mathcal{O}$。在 CNN 骨干网络之后，它们被集成到一个统一的框架中，如图 1 所示。

2D Detection. The 2D detection module is the basic module that stabilizes the feature learning and also reveals regions of interest to the subsequent geometric reasoning modules.
2D Detection. 2D 检测模块是稳定特征学习的基本模块，并且还显示随后的几何推理模块感兴趣的区域。

stabilize ['steɪbəlaɪz]：vt. 使稳固，使安定 vi. 稳定，安定

We leverage the design of the detection component in (Teichmann et al. 2016), which combines fast regression (Redmon et al. 2016) and size-adaptive RoiAlign (He et al. 2017), to achieve a convincing speed-accuracy ratio. An input image $I$ of size $W\times H$ is divided into an $S_x\times S_y$ grid $\mathcal{G}$, where a cell is indicated by $\mathbf{g}$. The output feature map of the backbone is also reduced to $S_x\times S_y$. Each pixel in the feature map corresponding to an image grid cell yields a prediction. The 2D prediction of each cell $\mathbf{g}$ contains the confidence that an object of interest is present and the 2D bounding box of this object, namely, $(P{r}_{obj}^{\mathbf{g}},B_{2d}^{\mathbf{g}})$, indicated by a superscript $\mathbf{g}$. The 2D bounding box $B_{2d}=({\delta }_{xb},{\delta }_{yb},w,h)$ is represented by the offsets $({\delta }_{xb},{\delta }_{yb})$ of its center $\mathbf{b}$ to the cell $\mathbf{g}$ and the 2D box size $(w,h)$.
我们利用 (Teichmann et al. 2016) 中的检测组件的设计，其结合了快速回归 (Redmon et al. 2016) 和尺寸自适应 RoiAlign (He et al. 2017)，以实现令人信服的速度准确率。输入图像 $I$，大小 $W\times H$ 被分为 $S_x\times S_y$ grid $\mathcal{G}$，其中一个单元格由 $g$ 表示。骨干网络的输出特征映射也减少到 $S_x\times S_y$。 特征图中与图像网格单元对应的每个像素产生预测。每个单元 $g$ 的 2D 预测包含感兴趣的物体存在的置信度以及该物体的 2D 边界框，即 $(P{r}_{obj}^{\mathbf{g}},B_{2d}^{\mathbf{g}})$，用上标 $g$ 表示。2D 边界框 $B_{2d}=({\delta }_{xb},{\delta }_{yb},w,h)$ 由其 $({\delta }_{xb},{\delta }_{yb})$ 表示中心 $\mathbf{b}$ 到单元格 $\mathbf{g}$ 偏移量和 2D 框大小 $(w,h)$。

superscript ['suːpəskrɪpt; 'sjuː-]：adj. 标在上方的 n. 上标

The predicted 2D bounding boxes are taken as inputs of the RoiAlign (He et al. 2017) layers to extract early features with high resolutions to refine the predictions and reduce the performance gap between this fast detector with proposal-based detectors.
将预测的 2D 边界框作为 RoiAlign (He et al. 2017) 层的输入，以提取具有高分辨率的早期特征，以改进预测并减少该快速检测器与基于候选区域的检测器之间的性能差距。

Instance-Level Depth Estimation. The IDE subnetwork estimates the depth of the ABBox-3D center $Z_c$. Given the divided grid $\mathcal{G}$ in the feature map from backbone, each grid cell $\mathbf{g}$ predicts the 3D central depth of the nearest instance within a distance threshold ${\delta }_{scope}$, considering depth information, i.e., closer instances are assigned for cells, as illustrated in Fig. 3 (a). An example of predicted instance depth for each cell is shown in Fig. 3 (c).
Instance-Level Depth Estimation. IDE 子网估计 ABBox-3D 中心的深度 $Z_c$。给定来自骨干网络的特征图中的划分网格 $\mathcal{G}$，每个网格单元 $\mathbf{g}$ 预测距离阈值 ${\delta }_{scope}$ 内最近实例的 3D 中心深度，考虑深度信息，即为 cell 分配更近的实例，如 Fig. 3 (a) 所示。每个 cell 的预测实例深度的例子如 Fig. 3 (c) 所示。

Figure 3: Instance depth. (a) Each grid cell $\mathbf{g}$ is assigned to a nearest object within a distance $({\delta }_{scope}$ to the 2D bbox center ${\mathbf{b}}_i$. Objects closer to the camera are assigned to handle occlusion. Here $Z_c^1<Z_c^2$. (b) An image with detected 2D bounding boxes. (c) Predicted instance depth for each cell.

The IDE module consists of a coarse regression of the region depth regardless of the scales and specific 2D location of the object, and a refinement stage that depends on the 2D bounding box to extract encoded depth features at exactly the region occupied by the target, as illustrated in Fig. 4.
IDE 模块包括区域深度的粗略回归，无论物体的尺度和特定 2D 位置如何，以及依赖于 2D 边界框以在目标占据的区域提取编码深度特征的改进阶段，如图 4 所示。

Figure 4: Instance depth estimation subnet. This shows the inference of the red cell.

coarse [kɔːs]：adj. 粗糙的，粗俗的，下等的
depth [depθ]：n. 深度，深奥
delta ['deltə]：n. (河流的) 三角洲，德耳塔 (希腊字母的第四个字)
refine [rɪ'faɪn]：vt. 精炼，提纯，改善，使...文雅

Grid cells in deep feature maps from the CNN backbone have larger receptive fields and lower resolution in comparison with that of shallow layers. Because they are less sensitive to the exact location of the targeted object, it is reasonable to regress a coarse depth offset $Z_{cc}$ from deep layers. Given the detected 2D bounding box, we are able to perform RoiAlign to the region containing an instance in early feature maps with a higher resolution and a smaller receptive field. The aligned features are passed through fully connected layers to regress a ${\delta }_{Z_c}$ in order to refine the instance-level depth value. The final prediction is $Z_c=Z_{cc}+{\delta }_{Z_c}$.
来自 CNN 骨干网络的深度特征图中的网格单元与浅层特征相比具有更大的感受野和更低的分辨率。因为它们对目标物体的确切位置不太敏感，所以从深层回归粗糙深度偏移 $Z_{cc}$ 是合理的。给定检测到的 2D 边界框，我们能够对包含具有更高分辨率和更小感受野的早期特征图中的实例的区域执行 RoiAlign。对齐的特征通过全连接层以回归 ${\delta }_{Z_c}$，以便细化实例级深度值。最终预测是 $Z_c=Z_{cc}+{\delta }_{Z_c}$。

3D Location Estimation. This subnetwork estimates the location of 3D center $\mathbf{C}=(X_c,Y_c,Z_c)$ of an object of interest in each grid $\mathbf{g}$. As illustrated in Fig. 2, the 2D center $\mathbf{b}$ and the 2D projection $\mathbf{c}$ of $\mathbf{C}$ are not located at the same position due to perspective transformation. We first regress the projection $\mathbf{c}$ and then backproject it to the 3D space based on the estimated depth $Z_c$.
3D Location Estimation. 此子网络估计每个网格 $\mathbf{g}$ 中感兴趣目标的 3D 中心 $\mathbf{C}=(X_c,Y_c,Z_c)$ 的位置。如图 2 所示，由于透视变换，2D 中心 $\mathbf{b}$ 和 3D center $\mathbf{C}$ 的投影 $\mathbf{c}$ 不在同一位置。我们首先回归投影 $\mathbf{c}$，然后根据估计的深度 $Z_c$ 将其反投影到 3D 空间。

In a calibrated image, we elaborate the projection mapping from a 3D point $\mathbf{X}=(X,Y,Z)$ to a 2D point $\mathbf{x}=(u,v),{\psi }_{3D\mapsto 2D}:\mathbf{X}\mapsto \mathbf{x}$, by
在校准图像中，我们详细说明了从 3D 点 $\mathbf{X}=(X,Y,Z)$ 到 2D 点的投影映射 $\mathbf{x}=(u,v),{\psi }_{3D\mapsto 2D}:\mathbf{X}\mapsto \mathbf{x}$，by

$$u=f_x\ast X/Z+p_x,v=f_y\ast Y/Z+p_y\text{\hspace{1em}(2)}$$

where $f_x$ and $f_y$ are the focal length along $X$ and $Y$ axes, $p_x$ and $p_y$ are coordinates of the principle point. Given known $Z$, the backprojection mapping ${\psi }_{2D\mapsto 3D}:(\mathbf{x},Z)\mapsto \mathbf{X}$ takes the form:
其中 $f_x$ and $f_y$ 是 $X$ and $Y$ 轴的焦距，$p_x$ and $p_y$ 是主点的坐标。给定已知的 $Z$，反投影映射 ${\psi }_{2D\mapsto 3D}:(\mathbf{x},Z)\mapsto \mathbf{X}$ 采用以下形式：

$$X=(u-p_x)\ast Z/f_x,Y=(v-p_y)\ast Z/f_y\text{\hspace{1em}(3)}$$

elaborate [ɪ'læb(ə)rət]：adj. 精心制作的，详尽的，煞费苦心的 vt. 精心制作，详细阐述，从简单成分合成 (复杂有机物) vi. 详细描述，变复杂

Since we have obtained the instance depth $Z_c$ from the IDE module, the 3D location $\mathbf{C}$ can be analytically computed using the 2D projected center $\mathbf{c}$ according to Equation 3. Consequently, the 3D estimation problem is converted to a 2D keypoint localization task that only relies on a monocular image.
由于我们已经从 IDE 模块获得实例深度 $Z_c$，因此可以使用根据等式 3 的 2D 投影中心 $\mathbf{c}$ 来分析地计算 3D 位置 $\mathbf{C}$。因此，3D 估计问题被转换为仅依赖于单眼图像 2D 关键点定位任务。

Similar to the IDE module, we utilize deep features to regress the offsets ${\delta }_{\mathbf{c}}=({\delta }_{x_c},{\delta }_{y_c})$ of a projected center $\mathbf{c}$ to the grid cell $\mathbf{g}$ and calculate a coarse 3D location ${\mathbf{C}}_s={\psi }_{3D\mapsto 2D}({\delta }_{\mathbf{c}}+\mathbf{g},Z_c)$. In addition, the early features with high resolution are extracted to regress the delta ${\delta }_{\mathbf{C}}$ between the predicted ${\mathbf{C}}_s$ and the groundtruth $\mathbf{C}$ to refine the final 3D location, $\mathbf{C}={\mathbf{C}}_s+{\delta }_{\mathbf{C}}$.
与 IDE 模块类似，我们利用深层特征来回归预测中心 $\mathbf{c}$ 到网格单元 $\mathbf{g}$ 的偏移 ${\delta }_{\mathbf{c}}=({\delta }_{x_c},{\delta }_{y_c})$，并计算粗略的 3D 位置 ${\mathbf{C}}_s={\psi }_{3D\mapsto 2D}({\delta }_{\mathbf{c}}+\mathbf{g},Z_c)$。此外，提取具有高分辨率的早期特征用于回归 the predicted ${\mathbf{C}}_s$ and the groundtruth $\mathbf{C}$ 之间的 the delta ${\delta }_{\mathbf{C}}$，来优化最终的 3D 位置，$\mathbf{C}={\mathbf{C}}_s+{\delta }_{\mathbf{C}}$。

3D Box Corner Regression

This subnetwork regresses eight corners, i.e., $\mathcal{O}=\{{\mathbf{O}}_k\},k=1,...,8$, in a local coordinate frame. Since each grid cell predicts a 2D bounding box in the 2D detector, we apply RoiAlign to the cell’s corresponding region in early feature maps with high resolution and regress the local corners of the 3D bounding box.
该子网在本地坐标系中对 8 个角进行回归，即 $\mathcal{O}=\{{\mathbf{O}}_k\},k=1,...,8$。由于每个网格单元预测 2D 检测器中的 2D 边界框，因此我们将 RoiAlign 应用于具有高分辨率的早期特征图中的单元的对应区域，并回归 3D 边界框的局部角。

In addition, regressing poses of 3D boxes in camera coordinate frame is ambiguous (Xu et al. 2018; Gao et al. 2018; Guizilini and Ramos 2018). Even the poses of two 3D boxes are different, their projections could be similar when observed from certain viewpoints. We are inspired by Deep3DBox (Mousavian et al. 2017), which regresses boxes in a local system according to the observation angle.
另外，在相机坐标系中回归 3D 框的姿势是模糊的 (Xu et al. 2018; Gao et al. 2018; Guizilini and Ramos 2018)。即使两个 3D boxes 的姿态不同，从某些观点观察时它们的投影也可能相似。我们受到 Deep3DBox (Mousavian et al. 2017)的启发，它根据观察角度对本地系统中的 boxes 进行回归。

We construct a local coordinate frame, where the origin is at the object’s center, the z-axis points straight from the camera to the center in bird’s eye view, the x-axis is on the right of z-axis, and the y-axis does not change, illustrated in Fig. 2 (c). The transformation from local coordinates to camera coordinates are involved with a rotation $\mathbf{R}$ and a translation $\mathbf{C}$, and we obtain ${\mathbf{O}}_k^{cam}=\mathbf{R}{\mathbf{O}}_k+\mathbf{C}$, where $O_k^{cam}$ are the global corner coordinates. This is a single mapping between the perceived and actual rotation, in order to avoid confusing the regression model.
我们构造一个局部坐标系，其中原点位于物体的中心，z 轴在鸟瞰图中从摄像机直接指向中心，x 轴在 z 轴的右侧，而 y 轴不会改变，Fig. 2 (c) 所示。从本地坐标到摄像机坐标的转换涉及 a rotation $\mathbf{R}$ and a translation $\mathbf{C}$，我们得到 ${\mathbf{O}}_k^{cam}=\mathbf{R}{\mathbf{O}}_k+\mathbf{C}$，其中 $O_k^{cam}$ 是全局角点坐标。这是感知旋转和实际旋转之间的单一映射，以避免混淆回归模型。

Loss Functions

Here we formally formulate four task losses for the above subnetworks and a joint loss for the unified network. All the predictions are modified with a superscript $\mathbf{g}$ for the corresponding grid cell $\mathbf{g}$. Groundtruth observations are modified by the $(\cdot )$ symbol.
在这里，我们用公式表示上述子网络的四个任务损失和统一网络的联合丢失。对于相应的网格单元 $\mathbf{g}$，所有预测都使用上标 $\mathbf{g}$ 进行表示。groundtruth 观察值由 $(\cdot )$ 符号表示。

2D Detection Loss. The object confidence is trained using softmax $(s\cdot )$ cross entropy $(CE)$ loss and the 2D bounding boxes $B_{2d}=(x_b,y_b,w,h)$ are regressed using a masked L1 distance loss. Note that $w$ and $h$ are normalized by $W$ and $H$. The 2D detection loss are defined as:
2D Detection Loss. 使用 softmax $(s\cdot )$ cross entropy $(CE)$ loss 训练物体置信度，使用掩模的 L1 距离损失回归 the 2D bounding boxes $B_{2d}=(x_b,y_b,w,h)$。Note that $w$ and $h$ are normalized by $W$ and $H$.

$$\begin{array}{rl}& {\mathcal{L}}_{conf}=C{E}_{\mathbf{g}\in \mathcal{G}}(s\cdot (P{r}_{obj}^{\mathbf{g}}),{Pr}_{obj}^{\mathbf{g}})\\ & {\mathcal{L}}_{bbox}=\sum _{\mathbf{g}}{\mathbb{I}}_{\mathbf{g}}^{obj}\cdot d(B_{2d}^{\mathbf{g}},B_{2d}^{\mathbf{g}})\\ & {\mathcal{L}}_{2d}={\mathcal{L}}_{conf}+w{\mathcal{L}}_{bbox}\end{array}\text{\hspace{1em}(4)}$$

where $P{r}_{obj}^{\mathbf{g}}$ and ${Pr}_{obj}^{\mathbf{g}}$ refer to the confidence of predictions and groundtruths respectively, $d(\cdot )$ refers to L1 distance and ${\mathbb{I}}_{\mathbf{g}}^{obj}$ masks off the grids that are not assigned any object. The mask function ${\mathbb{I}}_{\mathbf{g}}^{obj}$ for each grid $\mathbf{g}$ is set to 1 if the distance between $\mathbf{g}\mathbf{b}$ is less then ${\delta }_{scope}$, and 0 otherwise. The two components are balanced by $w$.
其中 $P{r}_{obj}^{\mathbf{g}}$ and ${Pr}_{obj}^{\mathbf{g}}$ 分别指代预测和 ground truth，$d(\cdot )$ 指的是 L1 距离和 ${\mathbb{I}}_{\mathbf{g}}^{obj}$ 掩盖未分配任何物体的网格。如果 $\mathbf{g}\mathbf{b}$ 之间的距离小于 ${\delta }_{scope}$，每个网格的掩码函数 ${\mathbb{I}}_{\mathbf{g}}^{obj}$ 设置为 1，否则为 0。这两个部分由 $w$ 平衡。

Instance Depth Loss. This loss is a L1 loss for instance depths:

$$\begin{array}{rl}& {\mathcal{L}}_{zc}=\sum _{\mathbf{g}}{\mathbb{I}}_{\mathbf{g}}^{obj}\cdot d(Z_{cc}^{\mathbf{g}},Z_c^{\mathbf{g}})\\ & {\mathcal{L}}_{z\delta }=\sum _{\mathbf{g}}{\mathbb{I}}_{\mathbf{g}}^{obj}\cdot d(Z_{cc}^{\mathbf{g}}+{\delta }_{Z_c}^{\mathbf{g}},Z_c^{\mathbf{g}})\\ & {\mathcal{L}}_{depth}=\alpha {\mathcal{L}}_{zc}+{\mathcal{L}}_{z\delta }\end{array}\text{\hspace{1em}(5)}$$

where $\alpha >1$ that encourages the network to first learn the coarse depths and then the deltas.
其中 $\alpha >1$ 鼓励网络首先学习粗糙深度，然后是增量。

3D Localization Loss. This loss sums up the L1 loss of 2D projection and 3D location:

$$\begin{array}{rl}& {\mathcal{L}}_c^{2d}=\sum _{\mathbf{g}}{\mathbb{I}}_{\mathbf{g}}^{obj}\cdot d(\mathbf{g}+{\delta }_{\mathbf{c}}^{\mathbf{g}},{\mathbf{c}}^{\mathbf{g}})\\ & {\mathcal{L}}_c^{3d}=\sum _{\mathbf{g}}{\mathbb{I}}_{\mathbf{g}}^{obj}\cdot d({\mathbf{C}}_s^{\mathbf{g}}+{\delta }_{\mathbf{C}}^{\mathbf{g}},{\mathbf{C}}^{\mathbf{g}})\\ & {\mathcal{L}}_{location}=\beta {\mathcal{L}}_c^{2d}+{\mathcal{L}}_c^{3d}\end{array}\text{\hspace{1em}(6)}$$

where $\beta >1$ to make it possible to learn the projected center first and then refine the final 3D prediction.
其中 $\beta >1$ 可以先学习投影中心，然后优化最终的 3D 预测。

Local Corner Loss. The loss is the sum of L1 loss for all corners:

$${\mathcal{L}}_{corners}=\sum _{\mathbf{g}}\sum _k{\mathbb{I}}_{\mathbf{g}}^{obj}\cdot d({\mathbf{O}}_k,{\mathbf{O}}_{\mathbf{k}})\text{\hspace{1em}(7)}$$

Joint 3D Loss. Note that in the above loss functions, we decouple the monocular 3D detection into several subtasks and respectively regress different components of the 3D bounding box. Nevertheless, the prediction should be as a whole, and it is necessary to establish a certain relationship among different parts. We formulate the joint 3D loss as the sum of distances of corner coordinates in the camera coordinate frame:
Joint 3D Loss. 请注意，在上述损失函数中，我们将单眼 3D 检测分离为若干子任务，并分别回归 3D 边界框的不同分量。然而，预测应该是一个整体，并且有必要在不同部分之间建立一定的关系。我们将联合 3D 损失表示为摄像机坐标系中角坐标的距离之和：

$${\mathcal{L}}_{joint}=\sum _{\mathbf{g}}\sum _k{\mathbb{I}}_{\mathbf{g}}^{obj}\cdot d({\mathbf{O}}_k^{cam},{\mathbf{O}}_{\mathbf{k}}^{cam})\text{\hspace{1em}(8)}$$

stereo [ˈsterɪəʊ]：n. 立体声，立体声系统，铅版，立体照片 adj. 立体的，立体声的，立体感觉的

Implementation Details

Network Setup. The architecture of MonoGRNet is shown in Fig. 1. We choose VGG-16 (Matthew and Rob 2014) as the CNN backbone, but without its FC layers. We adopt KittiBox (Teichmann et al. 2016) for fast 2D detection and insert a buffer zone to separate 3D reasoning branches from the 2D detector. In the IDE module, a depth encoder structure similar in DORN (Fu et al. 2018) is integrated to capture both local and global features. We present detailed settings for each layer in the supplemental material. There are 46 weighted layers in total, with only 20 weighted layers for the deepest path (i.e., from the input to the IDE output), due to the parallel 3D reasoning branches. In our design, there are 7.7 million parameters in all the 2D and 3D modules, which is approximately 6.2% of the fully connected layers in the original VGG-16.
Network Setup. MonoGRNet 的体系结构如图 1 所示。我们选择 VGG-16 (Matthew and Rob 2014) 作为 CNN 主干网络，但没有 FC 层。我们采用 KittiBox (Teichmann et al. 2016) 进行快速 2D 检测，并插入缓冲区以将 3D 推理分支与 2D 检测器分开。在 IDE 模块中，集成了类似于 DORN (Fu et al. 2018) 的深度编码器结构，以捕获局部和全局特征。我们提供补充材料中每个层的详细设置。由于并行的 3D 推理分支，总共有 46 个加权层，对于最深路径 (i.e., from the input to the IDE output) 仅有 20 个加权层。在我们的设计中，所有 2D 和 3D 模块中有 770 万个参数，大约是原始 VGG-16 中完全连接层的 6.2％。

Training. The VGG-16 backbone is initialized with the pretrained weights on ImageNet. In the loss functions, we set $w=\alpha =\beta =10$. L2 regularization is applied to the model parameters with a decay rate of 1e-5. We first train the 2D detector, along with the backbone, for 120K iterations using the Adam optimizer (Kingma and Ba 2015). Then the 3D reasoning modules, IDE, 3D localization and local corners, are trained for 80K iterations with the Adam optimizer. Finally, we use SGD to optimize the whole network in an end-to-end fashion for 40K iterations. The batch-size is set to 5, and the learning rate is 1e-5 throughout training. The network is trained using a single GPU of NVidia Tesla P40.
Training. VGG-16 主干网使用在 ImageNet 上预训练权重进行初始化。在损失函数中，我们设置 $w=\alpha =\beta =10$。L2 正则化应用于模型参数，衰减率为 1e-5。我们首先使用 Adam 优化器 (Kingma and Ba 2015) 训练 2D 检测器和骨干网，进行120K 迭代。然后使用 Adam 优化器对 3D 推理模块、IDE、3D 定位和局部角进行 80K 迭代训练。最后，我们使用 SGD 以端到端的方式优化整个网络，进行 40K 迭代。批量大小设置为 5，整个训练过程中学习率为 1e-5。 使用 NVidia Tesla P40 的单个 GPU 训练网络。

Experiment

We evaluate the proposed network on the challenging KITTI dataset (Geiger, Lenz, and Urtasun 2012), which contains 7481 training images and 7518 testing images with calibrated camera parameters. Detection is evaluated in three regimes: easy, moderate and hard, according to the occlusion and truncation levels. We compare our method with the state-of-art monocular 3D detectors, MF3D (Xu and Chen 2018) and Mono3D (Chen et al. 2016). We also present the results of a stereo-based 3D detector 3DOP (Chen et al. 2015) for reference. For a fair comparison, we use the train1/val1 split following the setup in (Chen et al. 2016; Chen et al. 2017), where each set contains half of the images.
我们在具有挑战性的 KITTI 数据集 (Geiger, Lenz, and Urtasun 2012) 上评估提出的网络，其中包含 7481 个训练图像和 7518 个测试图像，它们都是校准摄像机参数的。根据遮挡和截断程度，在三类图像中评估检测：容易，中等和困难。我们将我们的方法与最先进的单眼 3D 检测器 MF3D (Xu and Chen 2018) and Mono3D (Chen et al. 2016) 进行了比较。我们还提出了基于立体声的 3D 检测器 3DOP (Chen et al. 2015) 的结果供参考。为了公平比较，我们使用 train1 / val1 拆分 (Chen et al. 2016; Chen et al. 2017)，其中每组包含一半的图像。

regime [reɪ'ʒiːm]：n. 政权，政体，社会制度，管理体制

Metrics. For evaluating 3D localization performance, we use the mean errors between the central location of predicted 3D bounding boxes and their nearest ground truths. For 3D detection performance, we follow the official settings of KITTI benchmark to evaluate the 3D Average Precision (AP3D) at different Intersection of Union (IoU) thresholds.
Metrics. 为了评估 3D 定位性能，我们使用预测的 3D 边界框的中心位置与其最近的 ground truths 之间的平均误差。对于 3D 检测性能，我们遵循 KITTI 基准的官方设置来评估不同交并比 (IoU) 阈值的 3D 平均精度 (AP3D)。

3D Localization Estimation. We evaluate the three dimensional location errors (horizontal, vertical and depth) according to the distances between the targeting objects and the camera centers. The distances are divided into intervals of 10 meters. The errors are calculated as the mean differences between the predicted 3D locations and their nearest ground truths in meters. Results are presented in Fig. 5. The errors, especially for in the depth dimension, increase as the distances grow because far objects presenting small scales are more difficult to learn.
3D Localization Estimation. 我们根据目标物体和摄像机中心之间的距离来评估三维位置误差 (水平、垂直和深度)。距离分为 10 米的间隔。误差计算为预测的 3D 位置与其最近的 ground truths 之间的平均差异 (以米为单位)。 结果如图 5 所示。误差 (特别是在深度维度上的误差增加) 随着距离的增加而增加，因为呈现小尺度的远物体更难以学习。

Figure 5: 3D Localization Errors in the horizontal, vertical and depth dimensions according to the distances between objects and camera centers.

moderate ['mɒd(ə)rət]：adj. 稳健的，温和的，适度的，中等的，有节制的 vi. 变缓和，变弱 vt. 节制，减轻

The results indicate that our approach (red curve) outperforms Mono3D by a significant margin, and is also superior to 3DOP, which requires stereo images as input. Another finding is that, in general, our model is less sensitive to the distances. When the targets are 30 meters or farther away from the camera, our performance is the most stable, indicating that our network deals with far objects (containing small image regions) best.
结果表明，我们的方法 (红色曲线) 优于 Mono3D，并且优于 3DOP，3DOP 需要立体图像作为输入。另一个发现是，一般来说，我们的模型对距离不太敏感。当目标距离摄像机 30 米或更远时，我们的性能最稳定，这表明我们的网络最好处理远处的物体 (包含小图像区域)。

Interestingly, horizontal and vertical errors are an order of magnitude smaller than that of depth, i.e., the depth error dominants the overall localization error. This is reasonable because the depth dimension is not directly observed in the 2D image but is reasoned from geometric features. The proposed IDE module performs superior to the others for the easy and moderate regimes and comparable to the stereo-based method for the hard regime.
有趣的是，水平和垂直误差比深度误差小一个数量级，即深度误差主导整体定位误差。这是合理的，因为深度尺寸不是在 2D 图像中直接观察到的，而是由几何特征推导出来的。所提出的 IDE 模块在简单和适度的场景下表现优于其他模块，并且在困难场景下与 stereo-based 方法相当。

3D Object Detection. 3D detection is evaluated using the $A{P}_{3D}$ at 0.3, 0.5 and 0.7 3D IoU thresholds for the car class. We compare the performance with two monocular methods, Mono3D and MF3D. The results are reported in Table 1. Since the authors of MF3D have not published their validation results, we only report the $A{P}_{3D}$ at 0.5 and 0.7 presented in their paper. Experiments show that our method outperforms the state-of-art monocular detectors mostly and is comparable to the stereo-based method.
3D Object Detection. 3D 检测使用 $A{P}_{3D}$ 评估汽车类别的 3D IoU 阈值是 0.3，0.5 和 0.7。我们与两种单眼方法 Mono3D 和 MF3D 进行性能比较。结果报告在表 1 中。由于 MF3D 的作者尚未公布其验证结果，我们仅报告其论文中提供的 $A{P}_{3D}$ 0.5 和 0.7。实验表明，我们的方法优于大部分现有技术的单眼检测器，并且与 stereo-based 的方法相当。

Our network is designed for efficient applications and a fast 2D detector with no region proposal is adopted. The inference time achieves about 0.06 seconds per image on a Geforce GTX Titan X, which is much less than the other three methods. On the other hand, this design at some degree sacrifices the accuracy of 2D detection. Our 2D AP of the moderate regime at 0.7 IoU threshold is 78.14%, about 10% lower than the region proposal based methods that generate a large number of object proposals to recall as many groundtruth as possible. Despite using a relatively weak 2D detector, our 3D detection achieves the state-of-the-art performance, resorting to our IDE and 3D localization module. Note that the 2D detection is a replaceable submodule in our network, and is not our main contribution.
我们的网络专为高效应用而设计，采用无候选区域的快速 2D 检测器。在 Geforce GTX Titan X 上，每个图像的推理时间大约为 0.06 秒，远远低于其他三种方法。另一方面，这种设计在某种程度上牺牲了 2D 检测的准确性。我们在 0.7 IoU 阈值的中等难度数据的 2D AP 为 78.14％，比基于候选区域的方法低约 10%，基于候选区域的方法产生大量的候选区域以尽可能多的检测目标。尽管使用了相对较弱的 2D 检测器，采用我们的 IDE 和 3D 定位模块，我们的 3D 检测功能可以实现最先进的性能。 请注意，2D 检测是我们网络中可替换的子模块，并不是我们的主要贡献。

sacrifice ['sækrɪfaɪs]：n. 牺牲，祭品，供奉 vt. 牺牲，献祭，亏本出售 vi. 献祭，奉献
resort [rɪ'zɔːt]：n. 凭借，手段，度假胜地，常去之地 vi. 求助，诉诸，常去，采取某手段或方法

Table 1: 3D Detection Performance. Average Precision of 3D bounding boxes on the same KITTI validation set and the inference time per image. Note that the stereo-based method 3DOP is not compared but listed for reference
Table 1：3D 检测性能，KITTI 验证集上的 3D 边界框的平均精度和每张图像的推理时间。注意不比较基于 stereo的方法 3DOP，列出以供参考。

Local 3D Bounding Box Regression. We evaluate the regression of local 3D bounding boxes with the size (height, width, length) and orientation metrics. The height, width, length of a 3D bounding box can be easily calculated from its eight corners. The orientation is measured by the azimuth angles in the camera coordinate frame. We present the mean errors in Table 2. Our network demonstrates a better capability to learn the size and orientation of a 3D bounding box from merely photometric features. It is worth noting that in our local corner regression module, after RoiAlign layers, all the objects of interest are rescaled to the same size to introduce scale-invariance, yet the network still manages to learn their real 3D sizes. This is because our network explores the image features that convey projective geometries and semantic information including types of objects (e.g., SUVs are generally larger than cars) to facilitate the size and orientation estimation.
Local 3D Bounding Box Regression. 我们使用尺度 (高度、宽度、长度) 和方向度量来评估局部 3D 边界框的回归。3D 边界框的高度、宽度、长度可以从八个角轻松计算出来。方向由相机坐标系中的方位角测量。我们在表 2 中给出了平均误差。我们的网络表现出更好的能力，仅仅通过光度学特征来学习 3D 边界框的大小和方向。值得注意的是，在我们的局部角点回归模块中，在 RoiAlign 图层之后，所有感兴趣的物体被重新缩放到相同的大小以引入尺度不变性，但网络仍然设法学习它们的真实 3D 尺寸。这是因为我们的网络探索了传达投影几何和包括物体类型的语义信息 (例如，SUV 通常比汽车大) 的图像特征，便于尺寸和方向估计。

azimuth ['æzɪməθ]：n. 方位，方位角，偏振角
photometric [,fotə'mɛtrɪk]：adj. 测光的，光度计的，光度测定的

Table 2: 3D Bounding Box Parameters Error.

Qualitative Results. Qualitative visualization is provided for three typical situations, shown in Fig. 6. In common street scenes, our predictions are able to successfully recall the targets. It can be observed that even though the vehicles are heavily truncated by image boundaries, our network still outputs precise 3D bounding boxes. Robustness to such a corner case is important in the scenario of autonomous driving to avoid collision with lateral objects. For cases where some vehicles are heavily occluded by others, i.e., in (g), (h) and (i), our 3D detector can handle those visible vehicles but fails in detecting invisible ones. In fact, this is a general limitation of perception from monocular RGB images, which can be solved by incorporating 3D data or multi-view data to obtain informative 3D geometric details.
定性结果。 如图 6 所示为三种典型场景提供定性可视化。在常见的街景中，我们的预测能够成功地检测目标。 可以观察到，即使车辆被图像边界严重截断，我们的网络仍然输出精确的 3D 边界框。在自动驾驶的情况下，对于这种角落情形的鲁棒性是重要的，以避免与侧向物体碰撞。对于某些车辆被其他车辆严重遮挡的情况，i.e., in (g), (h) and (i)，我们的 3D 检测器可以处理那些可见的车辆，但未能检测到不可见的车辆。实际上，这是来自单眼 RGB 图像的感知的一般限制，其可以通过结合 3D 数据或多视图数据来获得信息性 3D 几何细节来解决。

collision [kə'lɪʒ(ə)n]：n. 碰撞，冲突，(意见，看法) 的抵触，(政党等的) 倾轧
lateral ['læt(ə)r(ə)l]：adj. 侧面的，横向的 n. 侧部，边音 vt. 横向传球

Figure 6: Qualitative Results. Predicted 3D bounding boxes are drawn in orange, while ground truths are in blue. Lidar point clouds are plotted for reference but not used in our method. Camera centers are at the bottom-left corner. (a), (b) and (c) are common cases when predictions recall the ground truths, while (d), (e) and (f) demonstrate the capability of our model handling truncated objects outside the image. (g), (h) and (i) show the failed detections when some cars are heavily occluded.

Ablation Study

A crucial step for localizing 3D center $\mathbf{C}$ is estimating its 2D projection $\mathbf{c}$, since $\mathbf{c}$ is analytically related to $\mathbf{C}$. Although the 2D bounding box’s center $\mathbf{b}$ can be close to $\mathbf{c}$, as is illustrated in Fig. 2 (a), it does not have such 3D significance. When we replace $\mathbf{c}$ with $\mathbf{b}$ in 3D reasoning, the horizontal location error rises from 0.27m to 0.35m, while the vertical error increases from 0.09m to 0.69m. Moreover, when an object is truncated by the image boundaries, its projection $\mathbf{c}$ can be outside the image, while $\mathbf{b}$ is always inside. In this case, using $\mathbf{b}$ for 3D localization can result in a severe discrepancy. Therefore, our subnetwork for locating the projected 3D center is indispensable.
定位 3D 中心 $\mathbf{C}$ 的关键步骤是估计其 2D 投影 $\mathbf{c}$，因为 $\mathbf{c}$ 在分析上与 $\mathbf{C}$ 相关。虽然 2D 边界框的中心 $\mathbf{b}$ 可以接近 $\mathbf{c}$，如图 2 (a) 所示，但它没有这样的 3D 意义。当我们在 3D 推理中用 $\mathbf{b}$ 替换 $\mathbf{c}$ 时，水平位置误差从 0.27m 上升到 0.35m，而垂直误差从 0.09m 增加到 0.69m。此外，当物体被图像边界截断时，其投影 $\mathbf{c}$ 可以在图像外部，而 $\mathbf{b}$ 总是在内部。在这种情况下，使用 $\mathbf{b}$ 进行 3D 定位可能会导致严重的差异。因此，我们用于定位投影 3D 中心的子网是必不可少的。

analytically [,ænə'lɪtɪkəli]：adv. 分析地，解析地
indispensable [ɪndɪ'spensəb(ə)l]：adj. 不可缺少的，绝对必要的，责无旁贷的 n. 不可缺少之物，必不可少的人
discrepancy [dɪs'krep(ə)nsɪ]：n. 不符，矛盾，相差

In order to examine the effect of coordinate transformation before local corner regression, we directly regress the corners offset in camera coordinates without rotating the axes. It shows that the average orientation error increases from 0.251 to 0.442 radians, while the height, width and length errors of the 3D bounding box almost remain the same. This phenomenon corresponds to our analysis that switching to object coordinates can reduce the rotation ambiguity caused by projection, and thus enables more accurate 3D bounding box estimation.
为了检查局部角回归之前坐标变换的效果，我们直接回归相机坐标中的角偏移而不旋转轴。它表明平均方向误差从 0.251 弧度增加到 0.442 弧度，而 3D 边界框的高度、宽度和长度误差几乎保持不变。这种现象对应于我们的分析，即切换到物体坐标可以减少由投影引起的旋转模糊，从而实现更准确的 3D 边界框估计。

Conclusion

We have presented the MonoGRNet for 3D object localization from a monocular image, which achieves superior performance on 3D detection, localization and pose estimation among the state-of-the-art monocular methods. A novel IDE module is proposed to predict precise instance-level depth, avoiding extra computation for pixel-level depth estimation and center localization, regardless of far distances between objects and camera. Meanwhile, we distinguish the 2D bounding box center and the projection of 3D center for a better geometric reasoning in the 3D localization.The object pose is estimated by regressing corner coordinates in a local coordinate frame that alleviates ambiguities of 3D rotations in perspective transformations. The final unified network integrates all components and performs inference efficiently.
我们提出了用于单眼图像中 3D 物体定位的 MonoGRNet，在最先进的单眼方法中它实现了 3D 检测、定位和姿态估计的卓越性能。提出了一种新颖的 IDE 模块来预测精确的实例级深度，避免了像素级深度估计和中心定位的额外计算，无论物体和相机之间的距离如何。同时，我们区分 2D 边界框中心和 3D 中心投影，以便在 3D 定位中获得更好的几何推理。通过回归局部坐标系中的角坐标来估计物体姿势，其减轻透视变换中的 3D 旋转的模糊性。 最终的统一网络集成了所有组件并有效地执行推理。

alleviate [ə'liːvɪeɪt]：vt. 减轻，缓和
ambiguity [æmbɪ'gjuːɪtɪ]：n. 含糊，不明确，暧昧，模棱两可的话

References

Monocular 3D Object Detection for Autonomous Driving
Multi-View 3D Object Detection Network for Autonomous Driving
3D Object Proposals for Accurate Object Class Detection
Multi-level Fusion Based 3D Object Detection from Monocular Images

WORDBOOK

KEY POINTS