计算机负数实现：趣谈补码

小亮： 小杨呀，考你个问题。

小杨： 我不听，我不听，我不听。

小亮： 非常有意思的，你听听。你说如果给你一个计算器，但只能算加法，那你减法该怎么办呀？

小杨： 这么神奇的吗，你难道有方法？

小亮： 其实原理很简单的，日常生活中我们其实一直都有用到的，你看一下现在闹钟几点了？

小杨： 8 点！

小亮： 那 3 小时前是几点呢？

小杨： 8 - 3 = 5，5 点！

小亮： 那 9 小时以后呢？

小杨： 嗯嗯，你等等，一五得五，二五一十，五一劳动节，8 + 9 - 12 = 5，还是 5 点！

小亮： 你为什么减去了一个 12 呀？

小杨： 小学老师这样教我的呀，至于为什么？Emm，因为总共只有 12 个数呀！

小亮： 就是这里，你完成了一个伟大的操作！模运算。你进行了模 12 操作，还有一个关键点，总共只有 12 个数！

小杨： 我是不是很厉害，嘻嘻嘻，但是… 然后呢？

小亮： 你想一想，8−3 和 8+9 的结果是一样的，而最开始我给你的计算器只能进行加法操作，所以再进一步，把 8−3 当做 8+(−3)，它和 8+9 的结果一致，所以…

小杨： 所以我们用 9 去表示 −3，然后如果想计算减法 8−3，就直接在计算器上输 8+9，就可以得到正确结果了！

小亮： bingo！但你忘了一个前提，就是计算器必须只能存 12 个数，它会自动进行取模操作。还有一个事，现在是 8 点，4 小时后呢？

小杨： 8 + 4 = 12，12 点！

小亮： 咦？你为什么不进行取模了，你在之前还多减了一个 12 呢？为了统一操作，我们每次都进行取模吧，12 - 12 = 0，这样也比较符合取模的含义，这样对 12 取模，意味着我们数的范围就是 0 到 11 了。

小杨： 好的，好的，我知道了，我现在只知道了 −3 可以用 9 表示，那我们想算 8−5 呢？−5 用多少表示呢？

小亮： 你自己拨动下表针看看，5 小时前和几小时后是等价的呢？

小杨： 我看看，7 点！算 8−5 的话，用 8 + 7 就可以了。好了，其他的我也知道了，来，我给你画张表。

小亮： 哇，你是怎么把这个对应关系列出来的？

小杨： 因为是模 12，所以 1 + 11 = 0，1 - 1 = 0，所以 −1 用 11 代替，2 + 10 等于 0，2 - 2 = 0，-2用 10 代替，其他也是这样的。

小亮： 棒棒棒，那现在计算会有一个问题的，之前的 8−3，8 - 5，结果都是正的，没有问题。那如果，3−5 呢？

小杨： 3−5，−5 对应 7，那就是 3 + 7 等于 10，看上边的表格，10 对应 −2，所以答案是 −2！骗子！明明没有问题！

小亮： 那你 5−3 呢？？？ −3 对应 9，5 + 9 = 2，看下上边的表格，这时候你咋不进行 2 对应 -10了。

小杨： 因为我知道 5 - 3 是正的，3 - 5 是负的，嘻嘻嘻。

小亮： 所以这就是问题所在了，既然要让计算器算，它肯定不知道是正的还是负的，所以这样肯定不行的。我们不能把每一个正数都对应一个负数，你看看下边这个表。

小杨： 3 - 5 和之前一样，−5 对应 7，那就是 3 + 7 等于 10，10 对应 −2，然后的话，5 - 3 = 2，−3 对应 9，5 + 9 = 2，2 对应 2，哇！这次没有问题了。

小亮： 是的，这次我们只是用一部分正数表示了负数，另一部分保持不变。每一个数都有了一个对应关系，9 不再是 9 了，它其实是 −3。但这有个缺点，给你一个数，你并不能立刻知道它代表几，只能去查表才会知道。

小杨： 对呀，我用的计算机能算的数的范围非常大呀，它内部不会也有这样一个表格吧。

小亮： 不不不，它实现了一种转换关系，给定一个数立马知道它代表的几。

小杨： 那会不会很复杂呀，我想听听。

小亮： 其实和那个钟表是一个意思的，计算机里寄存器存的位数是固定的，就像表盘的数是固定的。表盘里，11 点过 1 个小时后，就变成了 0 点，因为是进行的模 12 操作。如果寄存器只能存 4 位数字，那就总共可以表示 16 个数字，那么 15 再加 1 的话就变成了 0，那么怎么实现减法…

小杨： 我懂了，一样的道理，用一部分数字来表示负数就可以了!

小亮： 聪明！因为计算机里是都是用 2 进制存储的，我们来看看这些数字都长什么样子。

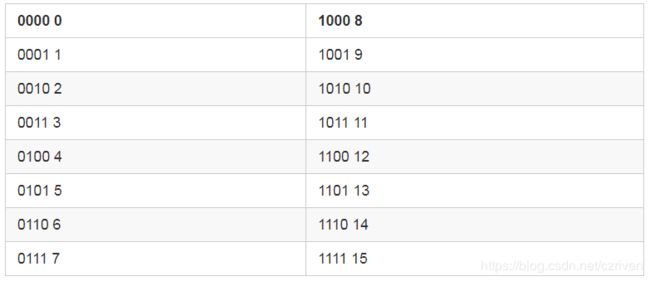
小杨： 那我来分一下吧！

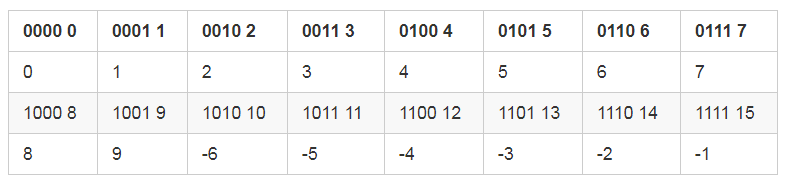
让我来算一个减法，7 - 4 = 7 + 12 模 16 = 3 ！哇，成功了！

小亮： 等等，你为什么搞了 8 个正数，只搞了 6 个负数呀。

小杨： 因为我喜欢！

小亮： 那这样又回到之前的问题了，如果我问 8 代表的正数还是负数？你是不是还是只能查表呀。

小杨： 对哦，那该怎么分呀。

小亮： 很自然呀，你看上边表格的二进制部分，最高位是不是有的是 0，有的是 1，我们把最高位是 1 的正数来表示负数，最高位是 0 的数表示正数，是不是就可以了。

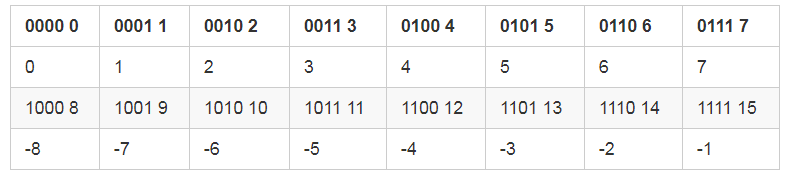
小杨： 对呀，这样的话，给我一个数，我就知道它是负的还是正的了，比如 13，二进制是 1101，开头是 1，那它代表的一定是一个负数。那开始你说可以直接知道它代表的是几，该怎么算呢？

小亮： 嗯嗯，你想一想，你得出表格的时候是怎么操作的呢？首先二进制开头是 0 的，它是几就代表几，就不讨论了。负数的话，你为什么用 12 表示 −4 呢？

小杨： 因为现在是模 16 的，所以两数和如果是 16 的话，就会变成 0。12 + 4 = 16 = 0，-4 + 4 = 0，所以 12 可以代替 −4。

小亮： 所以如果给你一个数，如果是二进制开头是 1，我们先确定它是一个负数，至于是负几，我们直接用 16 减它就够了！如果给你 13，我们看一下二进制是多少，1101，开头是 1 所以它是负数，负几呢？16 - 13 = 3，所以 13 代表 −3，看下上边的表格，是不是对的？

小杨： 等等，这个我一直知道呀，之前表盘的时候我就是这样算的呀。16 - 13，我们是为了用加法表示减法，这怎么又出来减法了。

小亮： 到了见证奇迹的时候了！让我们用二进制的形式看一下，16 - 13 = 1 0000 - 1101 = (1 + 1111) - 1101 = (1111 - 1101)+ 1 = 0010 + 1 = 0011 = 3。

小杨： 哪里奇迹了，1111 - 1101，这不又出现减法了。

小亮： 不不不，这步不用减法，只需要把 1101 按位取反就够了，也就是 0010！

小杨： 神奇！所以我来总结下，给我们一个数，如果二进制开头是 0，那就不管了，它是几就是几。如果开头是 1，那它代表负数，负几呢？按位取反，再加一就够了！但还有个问题，现在给我一个数我只能它代表几，但反过来，给我一个数，我怎么知道用几去代表它呢？如果给我 -3，我们用多少代表它呢？

小亮： 是同样的道理，13 + 3 = 16 = 0，-3 + 3 = 0，所以用 13 代表 -3。所以算的话，还是用 16 去减这个数，所以同样的推导，最后的结论是一样的，按位取反，末位加 1，-3 的话，根据推导我们是用 16 减去的 3，所以用 3 对应的 2 进制 0011，按位取反，1100，末位加一，1101，所以 -3 就用 1101 表示。

小杨： 哇，懂了懂了，这样完美的把加法和减法统一了，只不过计算前进行数字的转换就够了。

小亮： 对的，其实这就是补码，计算机中所有的整数都用补码存储，这样算减法用加法器就足够了。举个例子，3 的补码是 3 不变，也就是 0011，−4 的补码，4 的二进制按位取反末位加 1，也就是 0100 变成 1011，再加 1 变成 1100，所以算 3 - 4 = 3 + (-4) = 0011 + 1100 = 1111，1111 代表多少呢？首先肯定代表一个负数，然后按位取反末位加 1，就是 0001 了，所以结果就是 −1。

小杨： 我明白了，只要学会把一个数转成补码，然后补码再还原就够了，而且两个转换的方法还一样，按位取反，末位加 1，很清晰了。

小亮： 让我们回到真正的计算机里， 我们知道 int 一般情况是 4 个字节，也就是 32 位，一样的道理，我们把最高位是 0 的代表正数，最高位是 1 的代表负数，所以最大的正数就是 0111 1111 … 1111 1111，这个数代表多少呢？

小杨： 这个我知道，为了方便计算，先把它加 1，变成 1000 0000 … 0000 0000，这个是 2^{31} ，也就是 2147483648，然后减 1，就是 2147483647。

小亮： 那最小负数呢？

小杨： 最小负数的话，因为 1 开头代表负数，然后其他部分当然越小越好，所以就是 1000 0000 … 0000 0000，那它代表多少呢？直接套用公式，按位取反，末位加一，变成 1000 0000 … 0000 0000，它竟然又变了回来，之前算了这个数是 2^{31} ，也就是 2147483648，所以它代表 -2147483648，咦，怎么感觉负数比正数多了一个，没有对称呀？

小亮： 你想一下呀，0 开头的数和 1 开头的数，个数是不是一样的，但是 0 开头的数包括了 0，所以正数就少了一个咯。顺便再问你个问题，最小的负数是 −2147483648，那 -2147483648 - 1 是多少呢？

小杨： -2147483649！哈哈，开个玩笑，我知道你是问我计算机里边的情况。我来算一下，−2147483648 的补码是 1000 0000 … 0000 0000，−1 的补码是把 1 按位取反末位加 1，就是 11111111 1111 … 1111 1111，然后把这两个数加起来就是 0111 1111 … 1111 1111，这不是那个最大的正数吗，所以 −2147483648−1 是 2147483647！

小亮： 感觉你出师了呀，竟然没中套。这其实也很好理解对不对？

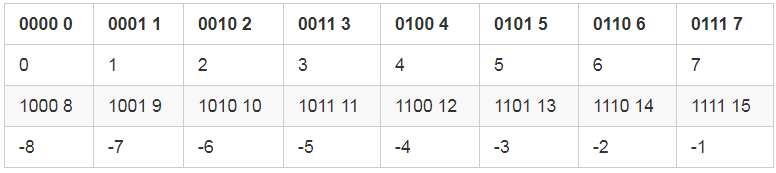
看上边的表格，这个只有 4 位，所以最大的数是 7，最小的数是 -8。上边的 7 后边是 −8 了，所以 −8 减 1，也就是 −8 前边那个数当然就是 7 了。

小杨： 其实这个表格化成圆其实更好理解了，就像表盘一样，哈哈。

小亮： 对的，总结一下，其实我们利用了寄存器存的位数是有限的，所以它到达最大的数以后会自动置零，相当于完成了取模操作，就像钟表一样，到了 11 点，之后又会从 0 点开始。然后我们再定义用哪些数表示正数，哪些数表示负数，从而完成了加法和减法的统一。并且做到了给一个数知道它的补码表示，知道补码，也可以算出它代表几。

小杨： 那计算机设计补码的时候就是这样想的吗？

小亮： 这我就不知道了，但可能和我想的一样？哈哈哈。最后留给你一个题，不用乘法除法也不用减法怎么求一个整数的相反数呢？在 int 范围内 -2147483648 * (1) 等于多少呢？详细应用可以参考 29 题-
链接: link.。

还有我们知道求中点，可以用 (start + end) / 2，但是这种做法可能会导致溢出。那么写成这样 (start + end) >>> 1 还会溢出吗？详细的可以参考 108 题-链接: link.。

转自：https://leetcode-cn.com/circle/article/bnmsCV/