【2013-10-3前】Matlab笔记1
前言
之前发过一篇文章BMP格式，主要是为了说明，在你用第三方软件，或API对图片进行操作时，其实首先要对图片的文件头进行解析，只是第三方软件或API已经帮你处理好了，你只需要关注图像处理的算法本身就行了！
Matlab是个不错的工具，可以快速有效的测试算法，但其本身只是个工具，真正重要的还是算法。本文主要是对参考文献做的笔记，方便自己查看。
第一部分 基础篇：
第一章：数据类型
double：a=3+2.3i
ceil--向正无穷取整、fix--向零取整、floor--向负无穷取整、round--四舍五入
字符串：
s='Hdu'
eval：执行字符串表示的表达式
ex：a=1;b=2;eval('c=a+b');
deblank：去掉字符串末尾的所有空格
ex：length(dablank('HDU '));
findstr：长字符中查找一个短字符
ex：findstr('How much','mu');
isstr、isletter、isspace、lower、upper、strcat、strvcat(竖直连接)、strcmp、strcmp(忽略大小写)、strjust(调整字符串矩阵对齐方式)
strmatch(寻找和目标字符串匹配的行)、strncmp(比较字符串前n个字符是否相同)、strrep(字符串查找和替换功能)、strtok(找出字符串第一个空格符前的字符串)
texlabel(把字符串转化成Tex软件的格式)、bin2dec_df(要求输入的参数为字符串)、bitget、bitset、bitand、bitor、bitxor
cell结构
A={'ABC'.11,'Zhang'};
cellplot(可画出一个图形来示意cell)、iscell
结构性
St.D=magic(3);St.s='ABC';St.c={'aa',1};
struct(建立一个结构体)、fieldnames(得到结构体中域的名称)、getfield(得到结构体中各域的内容)、rmfield(从结构体中删除一个域)
whos(查看变量的属性)、single(转为单精度)
cell-->char,cellstr<--字符串、字符串-->struct,char<--结构体、结构体-->struct2cell,cell2struct<--cell结构
变量
第二章：向量和矩阵运算
向量
v=1:0.1:2;
linspace(生成两个数之间的等间隔向量,默认个数100)
ex：linspace(1,2);
linspace(1,2,300); 、logspace(对数向量)、randperm(可产生1到N的随即自然数序列)、
isvector、length、cross(向量的外积)、dot(向量的内积)、detrend(用快速FFT去除向量中的线性趋势项)、wrev(反转向量顺序)、sort(排序)
集合
intersect(计算集合的交集)、ismember(集合中元素判断)、setdiff(两集合差集)、setxor(集合异或)、union(集合并集)、unique(去除集合中的重复元素)
矩阵
A=[];空矩阵、ones全1、zeros全0、eye单位矩阵、diag对角线矩阵、tril下三角、triu上三角、compan向量的伴随矩阵、hadamard哈达马矩阵、hankel汉克尔矩阵、hilb希尔伯特矩阵、invhilb逆希尔伯特矩阵、magic魔方矩阵、pascal帕斯卡矩阵、toeplitz托普利兹矩阵、wilkinson威尔金森特征值测试矩阵、vander范德蒙矩阵
size(计算行列数)、numel(矩阵所有元素)、ind2sub，sub2ind(不同索引格式的转换)、reshap(改变行列数)、cat(连接两个矩阵)、repmat(复制矩阵)、transpose(转置)、rot90(旋转90度的倍数)、fliplr，flipud(矩阵左右、上下翻转)、wshift，circshift(矩阵元素水平，竖直移动)、矩阵删除用---[]
eig(求矩阵本征值和本征向量)、det(矩阵行列式)、rank(矩阵的秩)
高维数组
ndims(计算数组维度)、squeeze(删除单独的维数)、shiftdim(移动数组维的顺序)、permute(改变数组的维数)、ndgrid(计算高维函数的离散形式)
第三章：表达式
ex：计算二元函数f(x,y)=xy+x^2+y^2(x,y定义在[-3,3]区间内)离散情况下的值
[x,y]=meshgrid(linspace(-3,3,200));f=x.*y+x.^2+y.^2;
Kronecker张量积，kron(x,y)
all(查找矩阵中非零元素的位置)、any(矩阵中列向量是否为0)、exist(检测变量或文件是否存在)、find(得到非零元素位置及大小关系)、isfinite(判断矩阵元素是否为有限值)、isequal(多个变量是否相等)、isnumeric(是否为数据型变量)、strel(创建用于腐蚀或膨胀的结构元素)、imerode(腐蚀)、imdilate(膨胀)
符号计算
s=sym('name');s=sym(var,flag);------vpa----d=9/7;r=vpa(d,8);
syms arg1,arg2 ... syms k positive
findsym(从表达式中查找符号变量)、pretty(把符号表达式转为手写格式)、simple(对符号表达式进行化简)、simplify(一般化简方法化简计算)、factor(表达式化成连乘积形式)、
expand(把表达式展开)、collet(降幂排列)、convert(exp),convert(sincos),convert(tan)分别以exp，sin&cos，和tan三种数学函数展开，mwcos2sin(给出一个利用cos与sin函数组成的化简结果)、radsimp(尽量给出一个复数形式的结果)、combine(trig),combine利用三角函数形式把高次三角函数转化为一次三角函数组合的形式、horner(表达式展开为重叠形式)、numden(把符号表达式化简为有理分式的形式)，subexpr(相同因子筛选和代换)，subs(符号表达式中变量赋值)、
ccode(把符号表达式转化为对应C语言代码)、fortran(转化为fortan语言)、diff(微分)、jacobian(雅可比)、int(不定积分和定积分)、dsolve(求解微分方程)、limit(计算极限)
多项式
Matlab把多项式降幂的系数提取出来，
maple(第一二类切比雪夫多项式，格根包尔，厄米，雅可比，拉盖尔、广义拉盖尔、勒让德)
mfun、roots(计算多项式函数的零点)、ploy2str(多项式系数to多项式标准字符串表达式，ex：poly2str(1:4,'x'))、polyval(多项式函数在某些特殊点的函数值)、conv(卷积)conv2、deconv(解卷积)、polyder(导数)、residue(公式转换)、corr(计算线相关系数)
ex1：符号表达式转化为字符串--f=dsolve('Df=f+sin(t)','f(pi/2)=0');f=char(f);
ex2：对变量的调用--f1=subs(sym('a*u+b'),{'a','b'},{'3','2'});f2=subs(sym('a*u+b'),{'3','2'},{'a','b'});
ex3：含变化参数的符号计算--a=2;v=int(sum(['x^',num2str(a),'+3']),1,2);
ex4：用函数实现赋值--syms x y;f=x^2+x+2;df=diff(sym('x^3+y^2*x'));x=1;y=2;fv=eval(df);
ex5：符号表达式转化--f=x^2+y*3;fun=inline(char(f));
ex6：数值型矩阵转化为符号性矩阵--symb=sym(magic(3));
ex7：复合函数应用--syms x y;f=1/(1+x^2);g=sin(y);fa=compose(f,g);fb=subs(f,x,g);
ex8：建立抽象函数--f=sym('f(x,y)');g=maple('map(g,x,y)');
第四章：交互及文件操作
input：在程序赋值及相应的地方写上注释；keyboard：对调试正在运行期间修改变量很有帮助。echo on，echo off，echo
profile：可详细地查看Matlab文件中每步消耗的时间
程序加速
数据类型：logical、char、int8、uint8、int16、uint16、int32、uint32、double，尽量不要用超过三维的数组，for、while、switch等代码编写要规范
复数书写：x=7+2i，避免用循环结构，预先分配数组zeros...，少用函数且一定要避免大数据量的参数传递
注释
%;换行...;%%分块;%**%区域注释
文件处理
函数：function [y1,y2,...]=function_name(x1,x2,...) 函数名要与文件名相同。
nargin：可以返回输入参数的个数
inline：内敛函数-与一般函数差不多，适用于表达式简单的函数
分段函数：s1=‘x.^2.*(x>=0&x<1)’;s2=‘cos([x-1]*pi).*(x>=0&x<1)’;s3=‘(-1)*x.^2./[x+2].*(x>=0&x<1)’;fx=inline([s1,'+',s2,'+',s3]);y=fx(linspace(0,4));plot(linspace(0,4),y);
load:数据读入函数dat、txt、mat、xls；importdata：读入数据文件、音频及图片文件的数据变量信息；dlmread：读取带有分隔符的ASCII文件到矩阵函数
wk1read：读入Lotus1-2-3文件；xlsread：读入Excel文件；fopen、fgetl：读取特殊数据；frewind：进行文件读取的时候，把指针放到文件头；
fscanf：从一个数据文件中按用户自定义的格式来读取格式化数据；写入函数：save，fwrite，fprintf，csvwrite，wk1write，xlswrite，cdfwrite，kmlwrite
图片文件：
imread--imwrite--print：把当前图形窗口上的内容打印到.jpg，.eps和.tif等格式的图形文件中
aviread--avifile记录一个avifile文件---auread--auwrite读写.au音频文件
文件批处理：
diary保存会话；fileparts返回文件名的信息；fullfile建立文件；inmem返回内存中的函数；ls同dir；matlabroot安装根目录；mkdir建立新路径；tempdir返回系统临时路径；type把M文件内容输入命令窗、what列出Matlab文件，filepart返回文件各个部分的信息
第二部分 科学计算：
第五章：线性方程组
| 函数名 | 说明 | 函数名 | 说明 |
| chol | 矩阵的cholesky分解 | lu | 矩阵的LU分解 |
| cholinc | 矩阵的不完全cholesky分解 | luinc | 矩阵的不完全LU分解 |
| diag | 提取矩阵对角元素 | norm | 矩阵或矢量的范数 |
| eig | 求本征值和本征向量 | normest | 求矩阵的最大范数矢量 |
| eye | 生成单位矩阵 | pinv | 求伪逆矩阵 |
| fliplr | 左右翻转矩阵 | qr | QR分解 |
| flipud | 上下翻转矩阵 | rank | 求矩阵的秩 |
| inv | 求逆矩阵 | trace | 矩阵对角元素的和（迹） |
线性方程组wiki
ex1：AX=B，A和B有相同的行数，则解为X=A\B;X=X';
ex2：消元法--rref(A)--rref可以得到矩阵的最简阶梯矩阵；列主元Gauss消去法解方程组A=[4,2,-6,4;3,1,5,2;2,3,2,-1;2,4,1,2];B=[2;0;0;8];X=CMGelim(A,B);
function X = CMGelim(A,B)
% 列主元Gauss消元法
% A是方矩阵
% b是列向量
% X是线性方程组AX=B的解。
if size(A,1)~=size(A,2); % 判断A是否为方矩阵
error('Matrix U must be square.');
end
N = size(A,1); % 返回未知数个数
Ap = [A,B]; % 生成增广矩阵
for n = 1:N-1;
[Y,Ind] = max(abs(Ap(n:N,n))); % 找出列主元的位置Ind
C = Ap(n,:); % 交换当前行和列主元对应的行
Ap(n,:) = Ap(Ind+n-1,:); % 交换当前行和列主元对应的行
Ap(Ind+n-1,:) = C; % 交换当前行和列主元对应的行
if Ap(n,n)==0; % 判断矩阵A是否奇异
error('Matrix is close to singular');
end
for k = n+1:N;
sc=Ap(k,n)/Ap(n,n); % 消元系数
Ap(k,n:N+1)=Ap(k,n:N+1)-sc*Ap(n,n:N+1); % 消元
end
end
X=uelim(Ap(:,1:N),Ap(:,N+1)); % 调用程序uelim.m进行回代过程ex3：LU分解-A=[3,2,2,5;2,2,3,5;2,3,4,2;2,-3,3,2];B=[2;0;0;9];[L,U]=lu(A);B1=L\B;X=uelim(U,B1);Delta=[A*X'-B]';
function X = uelim(U,B);
% U是上三角方矩阵。
% b是列向量。
% X是方程组AX=b的解。
if prod(diag(U))==0; % 判断矩阵U是否奇异
error('Matrix is close to singular or badly scaled.');
end
if size(U,1)~=size(U,2); % 判断U是否为方矩阵
error('Matrix U must be square.')
end
D = triu(U)-U;
if sum(abs(D(:)))>eps; % 判断U是否为上三角矩阵
error('Matrix U must be upper triangular.')
end
n = length(B); % 返回未知数个数
X(n) = B(n)/U(n,n); % 获得最后一个未知数的值
for k = n-1:-1:1;
X(k) = (B(k)-sum(X(k+1:n).*U(k,k+1:n)))/U(k,k); % 依次求解其它未知数
endex4：迭代法：1、雅可比迭代法：A=[9,4,2;3,8,2;2,3,7];B=[1,2,3];X0=[0,0,0];Y=Jacobi_iteration(A,B,X0);
function X = Jacobi_iteration(A,B,X0,kmax,tol);
% 雅可比(Jacobi)迭代法解线性方程组AX=B
if nargin == 4;
tol = 1e-6; % 设置默认精度
elseif nargin ==3;
tol = 1e-6;
kmax = 500;% 设置默认迭代次数
elseif nargin == 2;
tol = 1e-6;
kmax = 500;
X0 = zeros(size(B)); % 设置默认初值
end
n = length(B); % 获得未知数个数
if size(X0,1)2、高斯-赛德尔迭代1法：A=[9,2,2-4;2,8,2,-3;2,2,7,2;3,2,-2,9];B=[1;-1;2;1];X0=[0,0,0,];X=gauseid(A,B,X0);
function X = gauseid(A,B,X0,kmax,tol);
%This function is to find x = A^(-1)*B by Gauss–Seidel iteration.
% A是系数矩阵
% B是列向量
% X0是迭代初值
% kmax是最大迭代次数
% tol是预定的精度
if nargin == 4;
tol = 1e-6; % 设置默认精度
elseif nargin ==3;
tol = 1e-6;
kmax = 500;
elseif nargin == 2;
tol = 1e-6;
kmax = 500;
X0 = zeros(size(B));
end
n = length(B); % 获得未知数个数
if size(X0,1)ex5：共轭梯度法，bicg共个梯度、bicgstab稳定双共轭梯度、cgs复共轭梯度平方、gmres广义极小残差、lsqr共轭梯度的LSQR、minres最小残差、pcg预处理共轭梯度、qmr准最小残差、symmlq对称LQ
第六章：超越方程求解
函数解法：
ex1: solve求解
f = sym('a*x^2+b*x+c=0');
% f = 'a*x^2+b*x+c=0';
x = solve(f)
pretty(x)
xL = latex(x)
x =
-(b + (b^2 - 4*a*c)^(1/2))/(2*a)
-(b - (b^2 - 4*a*c)^(1/2))/(2*a)
和
其中a为未知数；将p,x和b作为常数看待
E1 = 'exp(-p*x)+b*sin(a)'; % 定义方程
E2 = '3*a+4*cos(a+pi)=0'; % 定义方程
a1 = solve(E1,'a') % 求解方程，并指定a为未知数
a2 = solve(E2,'a') % 求解方程，并指定a为未知数
a2d = double(a2) % 转化为双精度数据ex3：求非线性4元方程组的解
分析：第一个方程是线性的，而其他3个是非线性的
E1 = 'a+b+x=y*3'; % 定义方程
E2 = 'a*x-b*y=1'; % 定义方程
E3 = 'a*b+x*y=2'; % 定义方程
E4 = 'a+b=(x+y)^2'; % 定义方程
[a,b,x,y]=solve(E1,E2,E3,E4); % 解方程组
Solution = [a, b, x, y] % 合为一个矩阵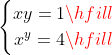
syms x y; % 定义符号变量
E1 = 'x*y=1'; % 定义方程
E2 = 'x^y=4'; % 定义方程
J = solve(E1,E2,x,y); % 求解方程，J是结构体
x=J.x % 显示x
y=J.y % 显示y
xd=double(x)
yd=[y]
figure;
x = linspace(-2,8,200);
y = lambertw(x);
plot(x,real(y),'k',x,imag(y),'k:');
set(gca,'Fontsize',12);
xlabel('\itx','Fontname','Times','Fontsize',18);
ylabel('lambertw({\itx})','Fontname','Times','Fontsize',18);
set(gca,'Position',[0.13 0.31 0.775 0.615]);
legend('Re','Im',0);
set(gcf,'Color','w');
syms x a b; % 定义符号变量
fx = x.^2-a*sin(x)+b; % 定义符号函数
fx = subs(fx,{a,b},{1,-2}); % 对a和b赋值
fx = char(fx); % 把fx转换为字符串
fx = strrep(fx,'^','.^'); % 把乘方运算转换为点运算
fx = inline(fx); % 定义内联函数
x1 = fzero(fx,0) % 求函数第1的零点
x2 = fzero(fx,2) % 求函数第2的零点
xt = -6:.1:6; % 产生[-6, 6]区间内等间距采样点
plot(xt,fx(xt)); % 绘制fx的曲线图
hold on;
plot(xlim,[0,0],'k:') % 绘制0刻度线
set(gca,'Position',[0.13 0.31 0.775 0.615]);
set(gcf,'color','w');ex6：求函数在【1，2】区间内的零点
xx = linspace(1,4,200);
yy = [xx.^2-4*sin(5*xx)]./[xx.^2+cos(xx)];
plot(xx,yy,'k');
fun = inline('abs([x^2-4*sin(5*x)]/[x^2+cos(x)])');
% % 转化为函数f(x)的绝对值
x01 = fminbnd(fun,1,1.5) % 计算最小值
x02 = fminbnd(fun,1.5,2) % 计算最小值
x03 = fminbnd(fun,1,4)
[x03, fval] = fminbnd(fun,1,4) % 计算最小值
hold on
plot(xx,abs(yy),'k:');
L=legend('{\itf}({\itx})','|{\itf}({\itx})|',0);
set(L,'Fontsize',18);
plot(x01,0,'r*','markersize',14); % 把解画到图上
plot(x02,0,'r*','markersize',14); % 把解画到图上
plot(x03,fval,'ro','markersize',14); % 把解画到图上
plot(x03,0,'ro','markersize',14);
set(gca,'Fontsize',18);
set(gcf,'Color','w');
，
其中
，初始条件为
xx = linspace(1,4,200); % 对自变量采样
for k=1:length(xx);
x=xx(k);
Ix=quad('sqrt(t).*sin(t).*exp(-t)',0,sin(6*x)); % 计算离散积分
y(k)=-2+x+Ix^2; % 得到方程1中函数的数值
end
subplot(121);
plot(xx,y); % 绘制曲线
hold on;
plot(xlim,[0,0],'r:') % 绘制0刻度线
[x01, f1] = dichotomy('fund1',1,4) % 解方程1
plot(x01,f1,'k*','markersize',12) % 用符号"*"标出方程1的解
set(gca,'Position',[0.13 0.41 0.327023 0.515]); % 重置坐标轴位置
set(gca,'Fontsize',12); % 重置字体大小
subplot(122);
[t,y]=ode45(@vdp1,[0 4],[2 0]); % 得到方程2中函数的数值
plot(t,y(:,1)); % 绘制曲线
hold on;
plot(xlim,[0,0],'r:') % 绘制0刻度线
[x02, f2] = dichotomy('fund2',1,4) % 解方程2
plot(x02,f2,'k*','markersize',12) % 用符号"*"标出方程2的解
set(gca,'Position',[0.577977 0.41 0.327023 0.515]); % 重置坐标轴位置
set(gca,'Fontsize',12); % 重置字体大小
set(gcf,'Color','w'); % 重置图形背景色
xx = linspace(1,3,200); % 对自变量采样
y = fund3(xx); % 计算个点的函数值
plot(xx,y); % 绘制函数f(x)曲线
hold on;
plot(xlim,[0,0],'r:'); % 绘制零刻度线
xr = parabola('fund3',1,2,3) % 抛物线法解方程
plot(xr,fund3(xr),'k*','markersize',12); % 绘制解对应的点
set(gca,'Fontsize',12)
set(gcf,'Color','w');
xx = linspace(0,6,200); % 对自变量采样
y = fund4(xx); % 计算个点的函数值
plot(xx,y); % 绘制函数f(x)曲线
hold on;
plot(xlim,[0,0],'r:'); % 绘制零刻度线
xr1 = Newtonm('fund4',1.5) %牛顿法求根，初始点是1.5
plot(xr1,fund4(xr1),'ks','markersize',12); % 绘制解对应的点
plot(1.5,fund4(1.5),'ks','markersize',12); % 绘制解对应的点
xr2 = Newtonm('fund4',3.5) %牛顿法求根，初始点是3.5
plot(xr2,fund4(xr2),'k*','markersize',12); % 绘制解对应的点
plot(3.5,fund4(3.5),'k*','markersize',12); % 绘制解对应的点
xr3 = Newtonm('fund4',5.5) %牛顿法求根，初始点是5.5
plot(xr3,fund4(xr3),'ko','markersize',12); % 绘制解对应的点
plot(5.5,fund4(5.5),'ko','markersize',12); % 绘制解对应的点
set(gca,'Fontsize',12)
set(gcf,'Color','w');
fun = inline('exp(x)-x-5'); % 定义方程中的函数f(x)
x0 = 3.5; % 第一初始值
x1 = 3; % 第二初始值
xr = secant(fun,x0,x1) % 用正割法解方程
xs = secant(fun,x1,x0) % 用正割法解方程
xq = fzero(fun,2) % 利用fzero函数作比较
x0 = 1; % 第一初始值
x1 = 3; % 第二初始值
xw = secant(fun,x0,x1) % 用正割法解方程
xa = steffenson(fun,x1) % 用steffenson法解方程
x0 = 1:.4:3.5;
for k = 1:length(x0); % 测试不同初始值对求解的影响
xt = x0(k);
xa = steffenson(fun,xt);
T(k,:)=[xt,xa];
end
T
第七章：数据拟合与插值
ex1：线性拟合
xk = 0:9;
yk = [2 3.4 5.6 8 11 12.3 13.8 16 18.8 19.9];
xk = 0:9;
yk = [2 3.4 5.6 8 11 12.3 13.8 16 18.8 19.9];
plot(xk,yk,'r+')
h=lsline
xd = get(h, 'XData');
yd = get(h, 'YData');
a = [yd(1)-yd(2)]/[xd(1)-xd(2)]
b = yd(1)-a*xd(1)
set(gcf,'Color','w')
set(gca,'Fontsize',16)
P = polyfit(xk,yk,1)x = 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000
y = 1.8000 1.7000 1.6000 1.5000 1.4000 1.2000 1.0000 0.8500 0.6700
z = 5.1000 5.4000 5.7000 6.0000 6.3000 6.4000 6.5000 6.7000 6.8000
M=[x',y',ones(9,1)];
d=z;
[X, resnorm, residual] = lsqlin(M,d)
X=X', resnorm, residual=residual'利用从2到5次多项式分别显示多项式系数和次数
x = 0:5; % 输入拟合x数据
y = [1 22 61 69 76 111]; % 输入拟合y数据
xp = 0:0.02:5; % 产生更密集的x轴数据
for N=2:5
P = polyfit(x,y,N); % N次多项式拟合
yp = polyval(P,xp); % 计算xp出的多项式值
plot(x,y,'r+',xp,yp,'k'); % 绘制数据点与拟合曲线
title(['n=',int2str(N)],'Fontsize',16); % 显示次数
for k=1:length(P);
text(1+k*0.4,k*10,['P(',num2str(k),...
')=',char(vpa(P(k),4))],...
'FOntsize',16); %显示所有多项式系数
end
set(gca,'Fontsize',14); %设置字体大小
set(gcf,'Color','w'); % 重置背景色
pause % 停顿
endxd =1 2 3 4 5 6 7 8 9 10
yd =3.5000 3.0000 2.6000 2.3000 2.1000 1.9000 1.7000 1.6000 1.50001.4000
load P0528 % 读入数据
c0 = [0,1,1]; % 初始值
c = lsqcurvefit('fit_model_a',c0,xd,yd) % 进行非线性拟合
plot(xd,yd,'r+','Markersize',10); % 利用原始数据绘图
hold on;
xp = linspace(min(xd),max(xd),200); % 生成原始数据范围内的等间距采样点
yp = fit_model_a(c,xp); % 利用拟合系数计算因变量数值
plot(xp,yp); % 绘制拟合曲线
set(gcf,'Color','w');
set(gca,'Fontsize',16);
c0 = [0,1,1]; % 初始值
c = lsqnonlin('fit_model_b',c0) % 进行非线性拟合ex5：拉格朗日插值
function y=lag_interp(x,xd,yd);
%Example:
% x=1:.1:4; % 待求点数据
% xd=1:4; % 插值点自变量数据
% yd=[2,1,3,4]; % 插值点因变量数据
% y=lag_interp(x,xd,yd); % 计算拉格朗日插值
% plot(x,y,'k',xd,yd,'ko','markersize',10);%绘制曲线
N = length(xd); % 插值点自变量数据长度
L = length(x); % 待求点数据长度
W = repmat(xd',1,L); % 生成矩阵W
X = repmat(x,N,1)-repmat(xd',1,L); % 矩阵Xt
y = 0; % 初始化y
for k = 1:N;
Xk = X;
Xk(k,:) = yd(k)*ones(1,L); % 生成矩阵Xk
Wk = xd(k)-W;
Wk(k,:) = 1;% 生成矩阵Wk
y = y+prod(Xk./Wk); % 累积求和
endx=1:.1:4; % 待求点数据
xd=1:4; % 插值点自变量数据
yd=[2,1,3,4]; % 插值点因变量数据
rand('state',0); % 设置随机数状态
dy = rand(1,4)-0.5; % 产生随机的dy值
y=hermite_interp(x,xd,yd,dy); % 插值计算
plot(x,y,'k',xd,yd,'ko','markersize',10); % 绘图
set(gca,'Fontsize',16)
set(gcf,'Color','w');
function y=hermite_interp(x,xd,yd,dy);
% Hermite插值
N = length(xd);% 计算插值点数据长度
L = length(x);% 计算待求点数据长度
X = repmat(x,N-1,1); % 扩展为矩阵X
y = 0; % 初始化y
for k = 1:N;
xt = xd;
xt(k) = []; % 去掉不满足条件的求和求积项
h=prod(1./[xd(k)-xt]);
h=h*prod([X-repmat(xt',1,L)]);
h = h.^2; % 计算h乘积因子
a = sum(1./[xd(k)-xt]); % 计算a乘积因子
y = y+h.*[(xd(k)-x)*(2*a*yd(k)-dy(k))+yd(k)];% 对y累加
endN = 5; % 设定采样点数
xd = linspace(-1,1,N); % 产生插值点
yd = 1./(1+25*xd.^2); % 产生插值点
x = linspace(-1,1,200); % 获得待求点坐标
y = 1./(1+25*x.^2); % 正确的结果
yL = lag_interp(x,xd,yd); % 拉格朗日插值
rand('state',0); % 设定随机数状态
dy = rand(1,N)-0.5; % 产生随机的一阶导数
yH=hermite_interp(x,xd,yd,dy); % 进行厄尔米特插值
subplot(221);
plot(x,yL,'k:',xd,yd,'kx','markersize',8);
hold on;
plot(x,y,'k','linewidth',1);
set(gca,'Fontsize',16);
text(-0.8,0.5,'{\itN} = 5','Fontsize',16);
xlabel('(a)');
subplot(222);
plot(x,yH,'k:',xd,yd,'kx','markersize',8);
hold on;
plot(x,y,'k','linewidth',1);
set(gca,'Fontsize',16);
text(-0.8,1,'{\itN} = 5','Fontsize',16);
xlabel('(b)');
%% N=10;
N = 13;
xd = linspace(-1,1,N);
yd = 1./(1+25*xd.^2);
x = linspace(-1,1,200);
y = 1./(1+25*x.^2);
yL = lag_interp(x,xd,yd);
rand('state',0);
dy = rand(1,N)-0.5;
yH=hermite_interp(x,xd,yd,dy);
subplot(223);
plot(x,yL,'k:',xd,yd,'kx','markersize',6);
hold on;
plot(x,y,'k','linewidth',1);
set(gca,'Fontsize',16);
text(-0.7,-2,'{\itN} = 13','Fontsize',16);
xlabel('(c)');
subplot(224);
plot(x,yH,'k:',xd,yd,'kx','markersize',8);
hold on;
plot(x,y,'k','linewidth',1);
set(gca,'Fontsize',16);
text(-0.7,150,'{\itN} = 13','Fontsize',16);
xlabel('(d)');
set(gcf,'Color','w');ex7：用不同方法计算函数在【0，5】上的分段插值
x = 0:.5:5; % 生成插值点自变量数据
% N=length(x); % 获得插值数据长度
% Ik=randperm(N); % 产生一个随机排序序列
% x = x(Ik); % 对x随机排序
y = x.^2.*cos(x); % 计算插值点因变量数值
xi = 0:.02:5; % 计算待求点自变量数据
% xi=fliplr(xi); % 左右翻转向量xi
method = {'nearest','linear','spline','pchip','cubic','v5cubic'}; % 插值方法名数组
for k=1:6;
subplot(3,2,k); % 分布子图顺序
yi = interp1(x,y,xi,char(method(k))); % 用不同方法分段插值
yg = xi.^2.*cos(xi); % 计算理论值
plot(x,y,'ko',xi,yi,'k:',xi,yg,'k'); % 画数据点及绘制曲线
text(2,5,char(method(k)),'Fontsize',16); % 输出插值方法
set(gca,'Fontsize',14); % 重置坐标轴字体
xlim([min(x),max(x)]); % 设定横轴范围
end
set(gcf,'Color','w');未完待续！
参考文献：
1、 MATLAB科学计算与可视化仿真宝典
2、 数值方法和MATLAB实现与应用