数据结构不要以为数组很简单——数组

一维数组

一维数组的CRUD

有关数组的CRUD其实是非常简单的。

//顺序表的.h文件
#include
using namespace std;
const int MAXSIZE = 20;
class SqList{
private:
    int *data;
    int length;
public:
    SqList();  //构造函数
    ~SqList(); // 析构函数
    void CreatList(int a[], int n); //创建顺序表
    void Display();  //输出顺序表中所有元素
    int GetLength(); //获取顺序表的长度
    bool GetElem(int, int &elem); // 获取顺序表中的某个元素
    bool ListInsert(int i, int elem); // 插入元素
    bool ListDelete(int i, int &elem); //删除元素
};

SqList::SqList(){
    cout<<"constract ok"< length){
        return false;
    }
    e = data[i-1];
    return true;
}

//插入元素
bool SqList::ListInsert(int i, int e){
    if(length == MAXSIZE) //保证插入位置正确
        return false;
    if(i < 1 || i > length+1)
        return false;
    if(i < length){
        for(int k = length-1; k >= i-1; k--)  //将插入位置之后的元素都向后移动一个位置
            data[k+1] = data[k];
    }
    data[i-1] = e;  //将待插入的元素赋值给插入位置
    length++;  //将顺序表的长度增加一个
    return true;
}

//删除元素
bool SqList::ListDelete(int i, int &e){
    if(length == 0)  //保证删除位置正确
        return false;
    if(i < 1 || i > length)
        return false;
    e = data[i-1];  //将要删除的元素保存给 e
    if(i < length){
        for(int k = i; k < length; k++){ //将删除位置后面的元素都向前移动一个位置
            data[k-1] = data[k];
        }
    }
    length--;  //将顺序表的长度删除一个
    return true;
}

void SqList::Display(){
    cout<<"display SqList:";
    for(int i = 0; i < length; i++){
        cout<

数组排序

https://www.cnblogs.com/still...

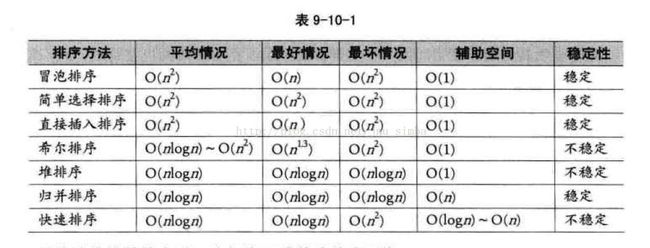
冒泡法

基本思想是:两两比较相邻记录的关键字,如果反序则交换

冒泡排序时间复杂度最好的情况为O(n),最坏的情况是O(n^2)

改进思路1：设置标志位，明显如果有一趟没有发生交换（flag = false)，说明排序已经完成

改进思路2：记录一轮下来标记的最后位置，下次从头部遍历到这个位置就Ok

选择排序

通过n-i次关键字之间的比较,从n-i+1 个记录中选择关键字最小的记录,并和第i(1<=i<=n)个记录交换之

尽管与冒泡排序同为O(n^2),但简单选择排序的性能要略优于冒泡排序

插入排序

将一个记录插入到已经排好序的有序表中, 从而得到一个新的,记录数增1的有序表

时间复杂度也为O(n^2), 比冒泡法和选择排序的性能要更好一些

希尔排序

先将整个待排元素序列分割成若干子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排

序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序（增量为1）。其时间复杂度为O(n^3/2),要好于直接

插入排序的O(n^2)

归并排序

假设初始序列含有n个记录,则可以看成n个有序的子序列,每个子序列的长度为1,然后两两归并,得到(不小于n/2的最小整数)个长度为2

或1的有序子序列,再两两归并,...如此重复,直至得到一个长度为n的有序序列为止,这种排序方法称为2路归并排序。 时间复杂度为

O(nlogn),空间复杂度为O(n+logn),如果非递归实现归并,则避免了递归时深度为logn的栈空间 空间复杂度为O(n)

快速排序

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。时间复杂度为O(nlogn)

堆排序

（见后）

总结

Code

#include
using namespace std;

void swap1(int *left, int *right)
{
    int temp = *left;
    *left = *right;
    *right = temp;
}

void swap2(int &left, int &right)
{
    int temp = left;
    left = right;
    right = left;
}

void swap3(int &left, int &right)
{
    if (&left != &right) 
    {
        left ^= right;
        right ^= left;
        left ^= right;
    }
}

/*****************************************************************/
/* 冒泡排序时间复杂度最好的情况为O(n),最坏的情况是O(n^2)
* 基本思想是:两两比较相邻记录的关键字,如果反序则交换 */

void BubbleSort1(int arr[], int num)
{
    int i, j;
    for (i = 0; i < num; i++)
    {
        for (j = 1; j < num - i; j++)
        {
            if (arr[j - 1] > arr[j])
                swap1(&arr[j - 1], &arr[j]);
        }
    }
}

// 改进思路：设置标志位，明显如果有一趟没有发生交换（flag = flase)，说明排序已经完成.
void BubbleSort2(int arr[], int num)
{
    int k = num;
    int j;
    bool flag = true;
    while (flag)
    {
        flag = false;
        for (j = 1; j < k; j++)
        {
            if (arr[j - 1] > arr[j])
            {
                swap1(&arr[j - 1], &arr[j]);
                flag = true;
            }
        }
        k--;
    }
}
//改进思路：记录一轮下来标记的最后位置，下次从头部遍历到这个位置就Ok
void BubbleSort3(int arr[], int num)
{
    int k, j;
    int flag = num;
    while (flag > 0)
    {
        k = flag;
        flag = 0;
        for (j = 1; j < k; j++)
        {
            if (arr[j - 1] > arr[j])
            {
                swap1(&arr[j - 1], &arr[j]);
                flag = j;
            }
        }
    }
}
/*************************************************************************/

/**************************************************************************/
/*插入排序: 将一个记录插入到已经排好序的有序表中, 从而得到一个新的,记录数增1的有序表
* 时间复杂度也为O(n^2), 比冒泡法和选择排序的性能要更好一些 */

void InsertionSort(int arr[], int num)
{
    int temp;
    int i, j;
    for (i = 1; i < num; i++)
    {
        temp = arr[i];
        for (j = i; j > 0 && arr[j - 1] > temp; j--)
            arr[j] = arr[j - 1];
        arr[j] = temp;
    }
}

/****************************************************************************/

/*希尔排序:先将整个待排元素序列分割成若干子序列（由相隔某个“增量”的元素组成的）分别进行
直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，
再对全体元素进行一次直接插入排序（增量为1）。其时间复杂度为O(n^3/2),要好于直接插入排序的O(n^2) */
void ShellSort(int *arr, int N)
{
    int i, j, increment;
    int tmp;
    for (increment = N / 2; increment > 0; increment /= 2)
    {
        for (i = increment; i < N; i++)
        {
            tmp = arr[i];
            for (j = i; j >= increment; j -= increment)
            {
                if (arr[j - increment] > tmp)
                    arr[j] = arr[j - increment];
                else
                    break;
            }
            arr[j] = tmp;
        }

    }
}

/**************************************************************************/

/* 简单选择排序(simple selection sort) 就是通过n-i次关键字之间的比较,从n-i+1
* 个记录中选择关键字最小的记录,并和第i(1<=i<=n)个记录交换之
* 尽管与冒泡排序同为O(n^2),但简单选择排序的性能要略优于冒泡排序 */

void SelectSort(int arr[], int num)
{
    int i, j, Mindex;
    for (i = 0; i < num; i++)
    {
        Mindex = i;
        for (j = i + 1; j < num; j++)
        {
            if (arr[j] < arr[Mindex])
                Mindex = j;
        }

        swap1(&arr[i], &arr[Mindex]);
    }
}

/********************************************************************************/
/*假设初始序列含有n个记录,则可以看成n个有序的子序列,每个子序列的长度为1,然后
* 两两归并,得到(不小于n/2的最小整数)个长度为2或1的有序子序列,再两两归并,...
* 如此重复,直至得到一个长度为n的有序序列为止,这种排序方法称为2路归并排序
* 时间复杂度为O(nlogn),空间复杂度为O(n+logn),如果非递归实现归并,则避免了递归时深度为logn的栈空间
* 空间复杂度为O(n) */


/*lpos is the start of left half, rpos is the start of right half*/
void merge(int a[], int tmp_array[], int lpos, int rpos, int rightn)
{
    int i, leftn, num_elements, tmpos;

    leftn = rpos - 1;
    tmpos = lpos;
    num_elements = rightn - lpos + 1;

    /*main loop*/
    while (lpos <= leftn && rpos <= rightn)
        if (a[lpos] <= a[rpos])
            tmp_array[tmpos++] = a[lpos++];
        else
            tmp_array[tmpos++] = a[rpos++];

    while (lpos <= leftn) /*copy rest of the first part*/
        tmp_array[tmpos++] = a[lpos++];
    while (rpos <= rightn) /*copy rest of the second part*/
        tmp_array[tmpos++] = a[rpos++];

    /*copy array back*/
    for (i = 0; i < num_elements; i++, rightn--)
        a[rightn] = tmp_array[rightn];
}


void msort(int a[], int tmp_array[], int left, int right)
{
    int center;

    if (left < right)
    {
        center = (right + left) / 2;
        msort(a, tmp_array, left, center);
        msort(a, tmp_array, center + 1, right);
        merge(a, tmp_array, left, center + 1, right);
    }
}



void merge_sort(int a[], int n)
{
    int *tmp_array;
    tmp_array = (int *)malloc(n * sizeof(int));

    if (tmp_array != NULL)
    {
        msort(a, tmp_array, 0, n - 1);
        free(tmp_array);
    }

    else
        printf("No space for tmp array!\n");
}

/************************************************************************************/
/* 堆是具有下列性质的完全二叉树:每个节点的值都大于或等于其左右孩子节点的值,称为大顶堆；
* 或者每个节点的值都小于或等于其左右孩子节点的值,称为小顶堆*/

/*堆排序就是利用堆进行排序的方法.基本思想是:将待排序的序列构造成一个大顶堆.此时,整个序列的最大值就是堆顶
* 的根结点.将它移走(其实就是将其与堆数组的末尾元素交换, 此时末尾元素就是最大值),然后将剩余的n-1个序列重新
* 构造成一个堆,这样就会得到n个元素的次大值.如此反复执行,便能得到一个有序序列了
*/
/* 时间复杂度为 O(nlogn),好于冒泡,简单选择,直接插入的O(n^2) */

// 构造大顶堆
#define leftChild(i) (2*(i) + 1)

void percDown(int *arr, int i, int N)
{
    int tmp, child;
    for (tmp = arr[i]; leftChild(i) < N; i = child)
    {
        child = leftChild(i);
        if (child != N - 1 && arr[child + 1] > arr[child])
            child++;
        if (arr[child] > tmp)
            arr[i] = arr[child];
        else
            break;
    }
    arr[i] = tmp;
}

void HeapSort(int *arr, int N)
{
    int i;
    for (i = N / 2; i >= 0; i--)
        percDown(arr, i, N);
    for (i = N - 1; i > 0; i--)
    {
        swap1(&arr[0], &arr[i]);
        percDown(arr, 0, i);
    }
}

树状数组（BIT）

https://www.cnblogs.com/xenny...

概念

在此之前要强调一下 BIT 的功能 ：可以解决大部分基于区间上的更新以及求和问题。

lowbit(x) = x & (-x) = 2^k

利用的负数的存储特性，负数是以补码存储的，对于整数运算 x&(-x)有

● 当x为0时，即 0 & 0，结果为0；
●当x为奇数时，最后一个比特位为1，取反加1没有进位，故x和-x除最后一位外前面的位正好相反，按位与结果为0。结果为1。
●当x为偶数，且为2的m次方时，x的二进制表示中只有一位是1（从右往左的第m+1位），其右边有m位0，故x取反加1后，从右到左第有m个0，第m+1位及其左边全是1。这样，x& (-x) 得到的就是x。 
●当x为偶数，却不为2的m次方的形式时，可以写作x= y * (2^k)。其中，y的最低位为1。实际上就是把x用一个奇数左移k位来表示。这时，x的二进制表示最右边有k个0，从右往左第k+1位为1。当对x取反时，最右边的k位0变成1，第k+1位变为0；再加1，最右边的k位就又变成了0，第k+1位因为进位的关系变成了1。左边的位因为没有进位，正好和x原来对应的位上的值相反。二者按位与，得到：第k+1位上为1，左边右边都为0。结果为2^k。
总结一下：x&(-x)，当x为0时结果为0；x为奇数时，结果为1；x为偶数时，结果为x中2的最大次方的因子。

而且这个有一个专门的称呼，叫做lowbit，即取2^k。

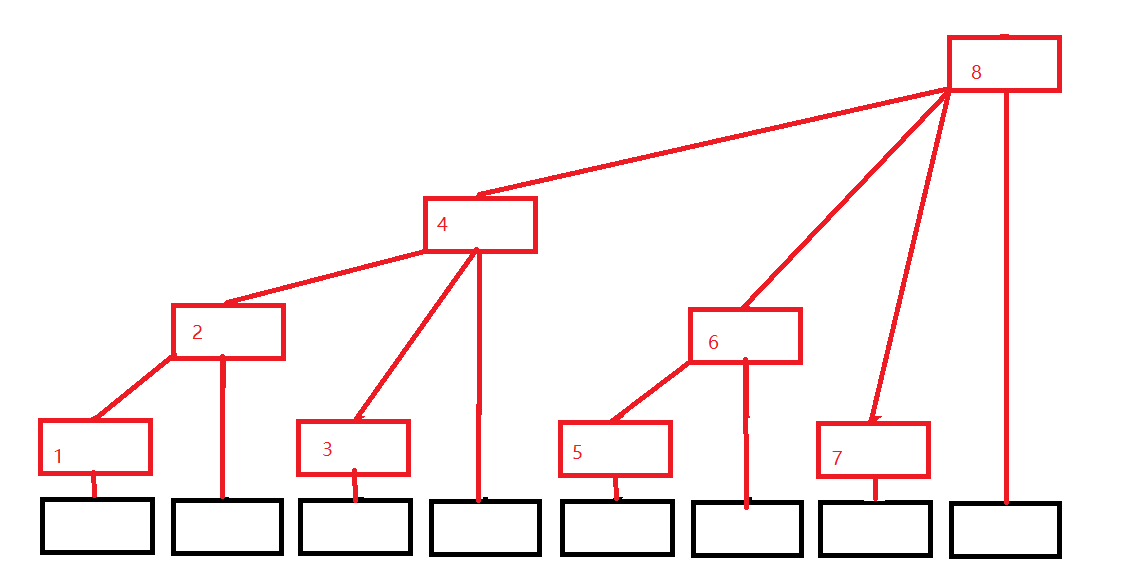
树状数组

黑色数组代表原来的数组（下面用A[i]代替），红色结构代表我们的树状数组(下面用C[i]代替)，发现没有，每个位置只有一个方框，令每个位置存的就是子节点的值的和，则有

• C[1] = A[1];
• C[2] = A[1] + A[2];
• C[3] = A[3];
• C[4] = A[1] + A[2] + A[3] + A[4];
• C[5] = A[5];
• C[6] = A[5] + A[6];
• C[7] = A[7];
• C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];

可以发现，这颗树是有规律的

$$ C[i] = A[i-2^{k}+1]+ A[i-2^{k}+2] + ...+A[i] 其中k为i的二进制中从最低位到高位连续零的长度 $$

例如i = 8(1000)时候，k = 3，可自行验证。

这个怎么实现求和呢，比如我们要找前7项和，那么应该是SUM = C[7] + C[6] + C[4];

而根据上面的式子，容易的出

$$ SUM_{i} = C[i]+ C[i-2^{k1}] + C[(i-2^{k1})-2^{k2}]+\dots $$

其实树状数组就是一个二进制上面的应用。

现在新的问题来了2^k该怎么求呢，之前已经提到过lowbit运算。

现在又有一个新问题：如何知道 A[1]+A[2]+...+A[i] 对应 C 中的哪些项之和呢？

$$ 记{\color{Red} SUM(1,x)=A[1]+...+A[x]} ,由于C[x]的覆盖长度是lowbit(x) 所以{\color{Red} C[x]=A[A-lowbit(x)+1]+...A[x]} $$

$$ {\color{Red} \therefore SUM(1,x)=A[1]+...+A[x]=A[1]+...+A[x-lowbit(x)]+A[x-lowbit(x)+1]+...+A[x]=SUM(1,x-lowbit(x))+C[x]} $$

Code

int n;
int a[1005],c[1005]; //对应原数组和树状数组

int lowbit(int x){
    return x&(-x);
}

void updata(int i,int k){    //在i位置加上k
    while(i <= n){
        c[i] += k;
        i += lowbit(i);
    }
}

int getsum(int i){        //求A[1 - i]的和
    int res = 0;
    while(i > 0){
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}
//两种getsum都可以
int getSum(int x){
    int sum = 0;
    for(int i = x; i > 0; i -= lowbit(i)){
        sum += c[i];
    }
    return sum;
}
//updata函数将第x个整数加上v
void upData(int x, int v){
    for(int i = x; i <= N; i += lowbit(i)){//i 必须取到N，N为元素个数.
        c[i] += x; //让C[i]加上v，然后让C[i+lowbit(i)]+v
    }
}

变形

单点更新，单点查询

传统数组即可。

单点更新，区间查询

问题描述：

C国的死对头A国这段时间正在进行军事演习，所以C国间谍头子Derek和他手下Tidy又开始忙乎了。A国在海岸线沿直线布置了N个工兵营地,Derek和Tidy的任务就是要监视这些工兵营地的活动情况。由于采取了某种先进的监测手段，所以每个工兵营地的人数C国都掌握的一清二楚,每个工兵营地的人数都有可能发生变动，可能增加或减少若干人手,但这些都逃不过C国的监视。
中央情报局要研究敌人究竟演习什么战术,所以Tidy要随时向Derek汇报某一段连续的工兵营地一共有多少人,例如Derek问:“Tidy,马上汇报第3个营地到第10个营地共有多少人!”Tidy就要马上开始计算这一段的总人数并汇报。但敌兵营地的人数经常变动，而Derek每次询问的段都不一样，所以Tidy不得不每次都一个一个营地的去数，很快就精疲力尽了，Derek对Tidy的计算速度越来越不满:"你个死肥仔，算得这么慢，我炒你鱿鱼!”Tidy想：“你自己来算算看，这可真是一项累人的工作!我恨不得你炒我鱿鱼呢!”无奈之下，Tidy只好打电话向计算机专家Windbreaker求救,Windbreaker说：“死肥仔，叫你平时做多点acm题和看多点算法书，现在尝到苦果了吧!”Tidy说："我知错了。。。"但Windbreaker已经挂掉电话了。Tidy很苦恼，这么算他真的会崩溃的，聪明的读者，你能写个程序帮他完成这项工作吗？不过如果你的程序效率不够高的话，Tidy还是会受到Derek的责骂的.

Input

第一行一个整数T，表示有T组数据。
每组数据第一行一个正整数N（N<=50000）,表示敌人有N个工兵营地，接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人（1<=ai<=50）。
接下来每行有一条命令，命令有4种形式：
(1) Add i j,i和j为正整数,表示第i个营地增加j个人（j不超过30）
(2)Sub i j ,i和j为正整数,表示第i个营地减少j个人（j不超过30）;
(3)Query i j ,i和j为正整数,i<=j，表示询问第i到第j个营地的总人数;
(4)End 表示结束，这条命令在每组数据最后出现;
每组数据最多有40000条命令

Output

1
10
1 2 3 4 5 6 7 8 9 10
Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End 

Case

6
33
59

Code

#include 
using namespace std;

int n,m;
int a[50005],c[50005]; //对应原数组和树状数组

int lowbit(int x){
    return x&(-x);
}

void updata(int i,int k){    //在i位置加上k
    while(i <= n){
        c[i] += k;
        i += lowbit(i);
    }
}

int getsum(int i){        //求A[1 - i]的和
    int res = 0;
    while(i > 0){
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}

int main(){
    int t;
    cin>>t;
    for(int tot = 1; tot <= t; tot++){
        cout << "Case " << tot << ":" << endl;
        memset(a, 0, sizeof a);
        memset(c, 0, sizeof c);
        cin>>n;
        for(int i = 1; i <= n; i++){
            cin>>a[i];
            updata(i,a[i]);   //输入初值的时候，也相当于更新了值
        }

        string s;
        int x,y;
        while(cin>>s && s[0] != 'E'){
            cin>>x>>y;
            if(s[0] == 'Q'){    //求和操作
                int sum = getsum(y) - getsum(x-1);    //x-y区间和也就等于1-y区间和减去1-(x-1)区间和
                cout << sum << endl;
            }
            else if(s[0] == 'A'){
                updata(x,y);
            }
            else if(s[0] == 'S'){
                updata(x,-y);    //减去操作，即为加上相反数
            }
        }

    }
    return 0;
}

区间更新，单点查询

如果题目是让你把x-y区间内的所有值全部加上k或者减去k，然后查询操作是问某个点的值，这种时候该怎么做呢。如果是像上面的树状数组来说，就必须把x-y区间内每个值都更新，这样的复杂度肯定是不行的，这个时候，就不能再用数据的值建树了，这里我们引入差分，利用差分建树。

假设我们规定A[0] = 0;

$$ A[i] = {\textstyle \sum_{j=1}^{i}}D[j];(其中D[j] = A[j]-A[j-1]) $$

即前面i项的差值和，这个有什么用呢？例如对于下面这个数组

• A[] = 1 2 3 5 6 9
• D[] = 1 1 1 2 1 3

如果我们把[2,5]区间内值加上2，则变成了

• A[] = 1 4 5 7 8 9
• D[] = 1 3 1 2 1 1

发现了没有，当某个区间[x,y]值改变了，区间内的差值是不变的，只有D[x]和D[y+1]的值发生改变

Code

int n,m;
int a[50005] = {0},c[50005]; //对应原数组和树状数组

int lowbit(int x){
     return x&(-x);
}

 void updata(int i,int k){    //在i位置加上k
     while(i <= n){
         c[i] += k;
        i += lowbit(i);
    }
}

int getsum(int i){        //求D[1 - i]的和，即A[i]值
    int res = 0;
  while(i > 0){
      res += c[i];
       i -= lowbit(i);
   }
   return res;
}

int main(){
    cin>>n;27     for(int i = 1; i <= n; i++){
        cin>>a[i];
       updata(i,a[i] - a[i-1]);   //输入初值的时候，也相当于更新了值
  }
   
   //[x,y]区间内加上k
   updata(x,k);    //A[x] - A[x-1]增加k
    updata(y+1,-k);        //A[y+1] - A[y]减少k
    
    //查询i位置的值
    int sum = getsum(i);

    return 0;
}

区间查询，区间查询

上面我们说的差值建树状数组，得到的是某个点的值，那如果我既要区间更新，又要区间查询怎么办。这里我们还是利用差分，由上面可知

$$ {\textstyle \sum_{i=1}^{n}}A[i]= {\textstyle \sum_{i=1}^{n}} {\textstyle \sum_{j=1}^{i}D[j]} $$

$$ A[1]+A[2]+...+A[n]=(D[1])+(D[1]+D[2])+...+(D[1]+D[2]+...+D[n])=n\times (D[1]+D[2]+...+D[n])-(0\times D[1]+1\times D[2]+...+(n-1)\times D[n]) $$

所以上式可以变为：

$$ {\textstyle \sum_{i=1}^{n}}A[i]=n\times {\textstyle \sum_{i}^{n}}=D[i]- {\textstyle \sum_{i=1}^{n}}(D[i]\times (i-1)) $$

Code

int n,m;
int a[50005] = {0};
int sum1[50005];    //(D[1] + D[2] + ... + D[n])
int sum2[50005];    //(1*D[1] + 2*D[2] + ... + n*D[n])

int lowbit(int x){
    return x&(-x);
}

void updata(int i,int k){
    int x = i;    //因为x不变，所以得先保存i值
    while(i <= n){
        sum1[i] += k;
        sum2[i] += k * (x-1);
        i += lowbit(i);
    }
}

int getsum(int i){        //求前缀和
    int res = 0, x = i;
    while(i > 0){
        res += x * sum1[i] - sum2[i];
        i -= lowbit(i);
    }
    return res;
}

int main(){
    cin>>n;
    for(int i = 1; i <= n; i++){
        cin>>a[i];
        updata(i,a[i] - a[i-1]);   //输入初值的时候，也相当于更新了值
    }

    //[x,y]区间内加上k
    updata(x,k);    //A[x] - A[x-1]增加k
    updata(y+1,-k);        //A[y+1] - A[y]减少k

    //求[x,y]区间和
    int sum = getsum(y) - getsum(x-1);

    return 0;
}

例题

题目1描述

给定一个有N个正整数的序列A（N<=10^5，A[i]<=10^5），对序列中的每一个数，求出序列中它左边比它小的数的列数

题目1解释

{ 2， 5，1，3， 4 } ,A[1] = 2;在A[1]左边比其小的数字有0个；A[2]=5，在A[2]左边比其下的数字有1个；A[5]=4，在A[5]左边比其小的数的个数为3

Code 1

#include 
#include 
const int maxn = 100010;
#define lowbit(i)  ((i)&(-i))
int C[maxn];  //树状数组
void UpDate(int x, int v){
    for(int i = 0; i < maxn; i+= lowbit(i)){
        C[i] += v; //让C[i]+v 然后让C[i+lowbit(i)]+v
    }
}
int GetSum(int x){
    int sum = 0;
    for(int i = x; i > 0; i -= lowbit(i)){
        sum += C[i];    //累计C[i],然后把问题缩小为SUM(1,i-lowbit(i))
    }
    return sum;
}
int main(){
    int n, x;
    scanf("%d",&n);
    memset(c, 0, sizeof(c));
    for(int i = 0; i < n; i++){
        scanf("%d",&x);
        update(x, 1);
        printf("%d\n", GetSum(x-1));
    }
    return 0;
}

本题是树状数组的最经典应用之一：统计序列中元素左边比该元素小的元素个数（小是题目定义）

扩展

离散化概念

若 A[i] <= N不成立（eg：A[i] <= 10^9 ）,好像树状数组没办法开那么大，时则不然。

其实A{ 520,999999999,14,666,888888} 我们只需要考虑他们之间的大小关系即可，也就是说，这个A序列和 B{ 2 , 5 , 1 , 3 , 4 }是等价的。{ 11 ， 111 ， 1 ， 11 }与{ 2，4, 1, 2 }。 需要做的是把1~N联系起来。

设置一个临时的结构体数组，用来存放输入序列元素的值以及原始序号，而在输入完成在之后将数组按照val从小到大排列，排序完成后按照“计算排名”的方式将排名“排名”根据原始序号pos存入一个新的数组即可。

Code

#include 
#include 
#include 
using namespace std;
const int manx = 100010;
#define lowbit(i) ((i)&(-i))
struct Node {
    int val;
    int pos;
}temp[maxn];
int A[maxn];
int C[maxn];

void UpData(int x, int v){
    for(int i = 0; i < maxn; i += lowbit(i)){
        C[i] += v;
    } 
}
int GetSum(int x){
    int sum = 0; 
    for(int i = x; i > 0; i -= lowbit(i)){
        sum += C[i];
    }
    return sum;
}
bool cmp(Node a, Node b){
    return a.val < b.val;
}
int main(){
    int n;
    scanf("%d",&n);
    memset(C, 0, sizeof(C));
    for(int i = 0; i < n; i++){
        scanf("%d",&temp[i].val);
        temp[i].pos = i;
    }
    sort(temp, temp + n, cmp);
    for(int i = 0; i < n; i++){
        if(i == 0 || temp[i].val != temp[i-1].val){
            A[temp[i].pos] = i + 1;//必须从1开始
        }else{
            A[temp[i].pos] = A[temp[i-1].pos];
        }
    }
    for(int i = 0; i < n; i++){
        UpDate(A[i], 1);
        printf("%d\n",GetSum(A[i]-1));
    }
    return 0;
}

需要注意的是离散化的方法只能用于离线查询，也就是我已经知道所有元素的值之后才可以进行查询。如果是在线的查询，虽然也不是没有办法，记录数据然后离散化。

二维数组的树状数组

把GetSum和UpDate循环改成两重循环.

Code

若求Aa 到 Ax 这个矩阵元素的元素之和 只需计算 GetSum(x,y)-GetSum(x-1,y)-GetSum(x,y-1)+GetSum(x-1,y-1)即可。

int C[maxn][maxn];

void UpDate(int x, int y, int v){
    for(int i = 0; i < maxn; i += lowbit(i)){
        for(int j = 0; j < maxn; i += lowbit(j)){
            C[i][j] += v;
        }
    }
}

int GetSum(int x, int y){
    int sum = 0;
    for(int i = 0; i > 0; i -= lowbit(i)){
        for(int j = 0; j > 0; j -= lowbit(i)){
            sum += C[i][j];
        }
    }
    return sum;
}

散列表（Hash）

https://blog.csdn.net/yyyljw/...

哈希表（Hash table，也叫散列表），是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。

记录的存储位置=f(关键字)

这里的对应关系f称为散列函数，又称为哈希（Hash函数），采用散列技术将记录存储在一块连续的存储空间中，这块连续存储空间称为散列表或哈希表（Hash table）。

哈希表hashtable(key，value) 就是把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字，然后就将该数字对数组长度进行取余，取余结果就当作数组的下标，将value存储在以该数字为下标的数组空间里。（或者：把任意长度的输入（又叫做预映射， pre-image），通过散列算法，变换成固定长度的输出，该输出就是散列值。这种转换是一种压缩映射，也就是，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，而不可能从散列值来唯一的确定输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。）

而当使用哈希表进行查询的时候，就是再次使用哈希函数将key转换为对应的数组下标，并定位到该空间获取value，如此一来，就可以充分利用到数组的定位性能进行数据定位。

数组的特点是：寻址容易，插入和删除困难；

而链表的特点是：寻址困难，插入和删除容易。

那么我们能不能综合两者的特性，做出一种寻址容易，插入删除也容易的数据结构？答案是肯定的，这就是我们要提起的哈希表，哈希表有多种不同的实现方法，我接下来解释的是最常用的一种方法——拉链法，我们可以理解为“链表的数组”，如图：

左边很明显是个数组，数组的每个成员包括一个指针，指向一个链表的头，当然这个链表可能为空，也可能元素很多。我们根据元素的一些特征把元素分配到不同的链表中去，也是根据这些特征，找到正确的链表，再从链表中找出这个元素。

Hash的应用

1、Hash主要用于信息安全领域中加密算法，它把一些不同长度的信息转化成杂乱的128位的编码,这些编码值叫做Hash值. 也可以说，Hash就是找到一种数据内容和数据存放地址之间的映射关系。

2、查找：哈希表，又称为散列，是一种更加快捷的查找技术。我们之前的查找，都是这样一种思路：集合中拿出来一个元素，看看是否与我们要找的相等，如果不等，缩小范围，继续查找。而哈希表是完全另外一种思路：当我知道key值以后，我就可以直接计算出这个元素在集合中的位置，根本不需要一次又一次的查找！

举一个例子，假如我的数组A中，第i个元素里面装的key就是i，那么数字3肯定是在第3个位置，数字10肯定是在第10个位置。哈希表就是利用利用这种基本的思想，建立一个从key到位置的函数，然后进行直接计算查找。

3、Hash表在海量数据处理中有着广泛应用。

Hash Table的查询速度非常的快，几乎是O(1)的时间复杂度。

hash就是找到一种数据内容和数据存放地址之间的映射关系。

散列法：元素特征转变为数组下标的方法。

我想大家都在想一个很严重的问题：“如果两个字符串在哈希表中对应的位置相同怎么办？”,毕竟一个数组容量是有限的，这种可能性很大。解决该问题的方法很多，我首先想到的就是用“链表”。我遇到的很多算法都可以转化成链表来解决，只要在哈希表的每个入口挂一个链表，保存所有对应的字符串就OK了。

散列表的查找步骤
当存储记录时，通过散列函数计算出记录的散列地址
当查找记录时，我们通过同样的是散列函数计算记录的散列地址，并按此散列地址访问该记录

关键字——散列函数（哈希函数）——散列地址

优点：一对一的查找效率很高；

缺点：一个关键字可能对应多个散列地址；需要查找一个范围时，效果不好。

散列冲突：不同的关键字经过散列函数的计算得到了相同的散列地址。

好的散列函数=计算简单+分布均匀（计算得到的散列地址分布均匀）

哈希表是种数据结构，它可以提供快速的插入操作和查找操作。

优缺点

优点：不论哈希表中有多少数据，查找、插入、删除（有时包括删除）只需要接近常量的时间即0(1）的时间级。实际上，这只需要几条机器指令。

哈希表运算得非常快，在计算机程序中，如果需要在一秒种内查找上千条记录通常使用哈希表（例如拼写检查器)哈希表的速度明显比树快，树的操作通常需要O(N)的时间级。哈希表不仅速度快，编程实现也相对容易。

如果不需要有序遍历数据，并且可以提前预测数据量的大小。那么哈希表在速度和易用性方面是无与伦比的。

缺点：它是基于数组的，数组创建后难于扩展，某些哈希表被基本填满时，性能下降得非常严重，所以程序员必须要清楚表中将要存储多少数据（或者准备好定期地把数据转移到更大的哈希表中，这是个费时的过程）。

元素特征转变为数组下标的方法就是散列法。散列法当然不止一种，下面列出三种比较常用的：

1，除法散列法
最直观的一种，上图使用的就是这种散列法，公式：

  index = value % 16 

学过汇编的都知道，求模数其实是通过一个除法运算得到的，所以叫“除法散列法”。

2，平方散列法
求index是非常频繁的操作，而乘法的运算要比除法来得省时（对现在的CPU来说，估计我们感觉不出来），所以我们考虑把除法换成乘法和一个位移操作。公式：

  index = (value * value) >> 28   （右移，除以2^28。记法：左移变大，是乘。右移变小，是除。）

如果数值分配比较均匀的话这种方法能得到不错的结果，但我上面画的那个图的各个元素的值算出来的index都是0——非常失败。也许你还有个问题，value如果很大，value * value不会溢出吗？答案是会的，但我们这个乘法不关心溢出，因为我们根本不是为了获取相乘结果，而是为了获取index。

3，斐波那契（Fibonacci）散列法

平方散列法的缺点是显而易见的，所以我们能不能找出一个理想的乘数，而不是拿value本身当作乘数呢？答案是肯定的。

1，对于16位整数而言，这个乘数是40503
2，对于32位整数而言，这个乘数是2654435769
3，对于64位整数而言，这个乘数是11400714819323198485

这几个“理想乘数”是如何得出来的呢？这跟一个法则有关，叫黄金分割法则，而描述黄金分割法则的最经典表达式无疑就是著名的斐波那契数列，即如此形式的序列：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377, 610， 987, 1597, 2584, 4181, 6765, 10946，…。另外，斐波那契数列的值和太阳系八大行星的轨道半径的比例出奇吻合。

对我们常见的32位整数而言，公式： 
        index = (value * 2654435769) >> 28

如果用这种斐波那契散列法的话，那上面的图就变成这样了：

注：用斐波那契散列法调整之后会比原来的取摸散列法好很多。

适用范围

快速查找，删除的基本数据结构，通常需要总数据量可以放入内存。

基本原理及要点

hash函数选择，针对字符串，整数，排列，具体相应的hash方法。 

碰撞处理，一种是open hashing，也称为拉链法；另一种就是closed hashing，也称开地址法，opened addressing。

散列冲突的解决方案：

1.建立一个缓冲区，把凡是拼音重复的人放到缓冲区中。当我通过名字查找人时，发现找的不对，就在缓冲区里找。

2.进行再探测。就是在其他地方查找。探测的方法也可以有很多种。

（1）在找到查找位置的index的index-1，index+1位置查找，index-2，index+2查找，依次类推。这种方法称为线性再探测。

（2）在查找位置index周围随机的查找。称为随机在探测。

（3）再哈希。就是当冲突时，采用另外一种映射方式来查找。

这个程序中是通过取模来模拟查找到重复元素的过程。对待重复元素的方法就是再哈希：对当前key的位置+7。最后，可以通过全局变量来判断需要查找多少次。我这里通过依次查找26个英文字母的小写计算的出了总的查找次数。显然，当总的查找次数/查找的总元素数越接近1时，哈希表更接近于一一映射的函数，查找的效率更高。

扩展

d-left hashing中的d是多个的意思，我们先简化这个问题，看一看2-left hashing。2-left hashing指的是将一个哈希表分成长度相等的两半，分别叫做T1和T2，给T1和T2分别配备一个哈希函数，h1和h2。在存储一个新的key时，同 时用两个哈希函数进行计算，得出两个地址h1[key]和h2[key]。这时需要检查T1中的h1[key]位置和T2中的h2[key]位置，哪一个 位置已经存储的（有碰撞的）key比较多，然后将新key存储在负载少的位置。如果两边一样多，比如两个位置都为空或者都存储了一个key，就把新key 存储在左边的T1子表中，2-left也由此而来。在查找一个key时，必须进行两次hash，同时查找两个位置。

问题实例（海量数据处理）

我们知道hash 表在海量数据处理中有着广泛的应用，下面，请看另一道百度面试题：

题目：海量日志数据，提取出某日访问百度次数最多的那个IP。
方案：IP的数目还是有限的，最多2^32个，所以可以考虑使用hash将ip直接存入内存，然后进行统计。

实现

https://www.cnblogs.com/liute...

散列表解决冲突的方式有多种，这里采用了分离链接法，除此外还有开放地址法和双散列。

Vocabulary类是用来储存单词的类，用于实现一个离线词典的数据方案，当然这并不是最高效的方法，但是我认为是比较容易理解的方法，对于初学哈希表的人来说还是比较容易接受的。

Code

/************************************************************************/
/* 文件说明：
/* 采用分离链接法实现哈希表，采用C++标准库中的vector和list实现
/*
/************************************************************************/
#include 
#include 
#include 

class Vocabulary;

int hash(const std::string & key, const int &tableSize);
int hash(const int & key, const int &tableSize);
//int hash(const Vocabulary & e, const int &tableSize);

namespace stl
{

    template 
    class HashTable
    {
    public:
        //typedef vector >::size_type SIZE;

        HashTable(int size = 101);     //初始化哈希表的大小
        ~HashTable(){}
        bool contains(const HashedObj & obj);
        bool insert(const HashedObj & obj);
        bool remove(const HashedObj & obj);
    private:

        std::vector > theList;   //哈希表
        int myhash(const HashedObj & obj) const;   //哈希函数
    };


    //函数定义
    template 
    HashTable::HashTable(int size /*= 101*/)
    {
        /*根据哈希表的大小分配vector的空间*/
        theList.reserve(size);
        theList.resize(size);
    }

    template 
    int HashTable::myhash(const HashedObj & obj) const
    {
        //根据object不同调用不同版本的hash重载函数
        return hash(obj, theList.size());
    }

/************************************************************************/
/* 函数名称：contains
/* 函数功能：查找指定对象是否在哈希表中
/* 返回值：存在返回true，不存在返回false
/************************************************************************/
    template 
    bool HashTable::contains(const HashedObj & obj)
    {
        int iHashValue = myhash(obj);
        const std::list & tempList = theList[iHashValue];

        std::list::const_iterator it = tempList.cbegin();

        for (; it != tempList.cend() && *it != obj; ++it);

        if(it != tempList.cend())
            return true;
        else
            return false;
    }

/************************************************************************/
/* 函数名称：insert
/* 函数功能：向hash表中插入元素，如果元素已经存在则返回false，不存在则在链表的最前面插入
/* 返回值：成功返回true，失败返回返回false
/************************************************************************/
    template 
    bool HashTable::insert(const HashedObj & obj)
    {
        int iHashValue = myhash(obj);

        std::list & tempList = theList[iHashValue];
        if (contains(obj))
        {
            return false;   //已经存在返回false
        }

        tempList.push_back(obj);
        return true;
    }

    /************************************************************************/
    /* 函数名称：remove
    /* 函数功能：从哈希表中删除指定元素，如果元素不存在则返回false
    /* 返回值：成功返回true，失败返回返回false
    /************************************************************************/
    template 
    bool HashTable::remove(const HashedObj & obj)
    {
        list & tempList = theList[myhash(obj)];
        auto it = find(tempList.begin(), tempList.end(), obj);
        if (it == tempList.end())
        {
            return false;
        }
        tempList.erase(it);
        return true;
    }
}


//hash表中存入单词表类，一个对象表示对应一个单词
class Vocabulary
{
public:
    Vocabulary(){ }

    ~Vocabulary(){ }

    void SetWordName(std::string name)
    {
        m_sWord = name;
    }

    void SetWordExplain(std::string explain)
    {
        m_sExplain = explain;
    }

    const std::string getName() const
    {
        return m_sWord;
    }

    Vocabulary(const Vocabulary &vc){

    }

    Vocabulary& operator= (const Vocabulary & v)
    {
        m_sWord = v.m_sWord;
        m_sExplain = v.m_sExplain;
        return *this;
    }




private:
    std::string m_sWord;
    std::string m_sExplain;
};

bool operator== (const Vocabulary & word1, const Vocabulary & word2)
{
    if (word1.getName() == word2.getName())
    {
        return true;
    }
    else
    {
        return false;
    }
}

bool operator!= (const Vocabulary & word1, const Vocabulary & word2)
{
    return !(word1 == word2);
}

int hash(const Vocabulary & e,const int &tableSize)
{
    return hash(e.getName(), tableSize);
}

int hash(const std::string & key, const int &tableSize)
{
    //采用公式：h = (k1*32 + k2) * 32 + k3，将其扩展到n次多项式
    long long int hashVal = 0;
    int count = 0;
    for (auto it = key.begin(); it != key.end(); ++it)
    {
        if (count++ % 2 == 0)
        {
            hashVal += (hashVal << 5) + *it;
        }

    }
    return hashVal %= tableSize;
}

int hash(const int & key, const int &tableSize)
{
    return key % tableSize;
}

Hash函数的构造

https://blog.csdn.net/qq_4080...

直接定址法

此类函数取关键码的某个线性函数值作为散列地址：hash ( key ) = a * key + b { a, b为常数 }

这类散列函数是一对一的映射，一般不会产生冲突。但是，它要求散列地址空间的大小与关键码集合的大小相同。

数字分析法

构造：对关键字进行分析，取关键字的若干位或其组合作哈希地址。
适于关键字位数比哈希地址位数大，且可能出现的关键字事先知道的情况。

例： 有80个记录，关键字为8位十进制数，哈希地址为2位十进制数

平方取中法

取关键字平方后中间几位作哈希地址。适于关键字位数不定情况。

具体方法：先通过求关键字的平方值扩大相近数的差别，然后根据表长度取中间的几位数作为散列函数值。又因为一个乘积的中间

几位数和乘数的每一位都相关，所以由此产生的散列地址较为均匀

折叠法

此方法把关键码自左到右分成位数相等的几部分，每一部分的位数应与散列表地址位数相同，只有最后一部分的位数可以短一些。

把这些部分的数据叠加起来，就可以得到具有该关键码的记录的散列地址。有两种叠加方法：

移位法 — 把各部分的最后一位对齐相加；

分界法 — 各部分不折断，沿各部分的分界来回折叠，然后对齐相加，将相加的结果当做散列地址。

一般当关键码的位数很多，而且关键码每一位上数字的分布大致比较均匀时，可用这种方法得到散列地址。

除数留余法

设散列表中允许的地址数为 m, 散列函数为：

hash ( key ) = key % p p <= m

若p取100，则关键字159、259、359互为同义词。我们选取的p值应尽可能使散列函数计算得到的散列地址与各位相关，根据经

验，p最好取一个不大于 m，但最接近于或等于 m 的质数 p, 或选取一 个不小于 20 的质因数的合数作为除数（比如8 = 222，2 是

8 的质因数，8 是合数）

示例：有一个关键码 key = 962148，散列表大小 m = 25，即 HT[25]。取质数 p= 23。散列函数 hash ( key ) = key % p。则散列地址

为 hash ( 962148 ) = 962148 % 23 = 12

可以按计算出的地址存放记录。需要注意的是，使用上面的散列函数计算出来的地址范围是 0到 22，因此，从23到24这几个散列地

址实际上在一开始是不可能用散列函数计算出来的，只可能在处理溢出时达到这些地址。

乘余取整法

使用此方法时，先让关键码 key 乘上一个常数 A (0 < A < 1)，提取乘积的小数部分。然后，再用整数 n 乘以这个值，对结果向下取

整，把它做为散列的地址。

随机数法

选择一个随机函数，取关键字的随机函数值为它的散列地址，即 hash(key) = random(key) ；其中random为伪随机函数，但要保证函

数值是在0到m-1之间

处理冲突

开放定址法（再散列）

基本思想：当关键字key的哈希地址p=H（key）出现冲突时，以p为基础，产生另一个哈希地址p1，如果p1仍然冲突，再以p为基础，产生另一个哈希地址p2，…，直到找出一个不冲突的哈希地址pi ，将相应元素存入其中。 这种方法有一个通用的再散列函数形式：

        Hi=（H（key）+di）% m   i=1，2，…，n

其中H（key）为哈希函数，m 为表长，di称为增量序列。增量序列的取值方式不同，相应的再散列方式也不同。

线性探测再散列

dii=1，2，3，…，m-1 冲突发生时，顺序查看表中下一单元，直到找出一个空单元或查遍全表。

二次探测再散列

di=12，-12，22，-22，…，k2，-k2 ( k<=m/2 ) 冲突发生时，在表的左右进行跳跃式探测，比较灵活。

伪随机探测再散列

di=伪随机数序列。 具体实现时，应建立一个伪随机数发生器，（如i=(i+p) % m），并给定一个随机数做起点。

再哈希

这种方法是同时构造多个不同的哈希函数： Hi=RH1（key） i=1，2，…，k

当哈希地址Hi=RH1（key）发生冲突时，再计算Hi=RH2（key）……，直到冲突不再产生。这种方法不易产生聚集，但增加了计算时间。

拉链法

基本思想: 将所有哈希地址为i的元素构成一个称为同义词链的单链表，并将单链表的头指针存在哈希表的第i个单元中，因而查找、插入和删除主要在同义词链中进行。链地址法适用于经常进行插入和删除的情况。

例如: 已知一组关键字（32，40，36，53，16，46，71，27，42，24，49，64），哈希表长度为13，哈希函数为：H（key）= key % 13，则用链地址法处理冲突的结果如图所示：

位置 Entry

    0
    1  -->  40 --> 27 --> 53
    2
    3  -->  16 --> 42
    4
    5
    6  -->  32 --> 71

    7
    8
    9
    10 -->  36 --> 49
    11 -->  24
    12 -->  64

建立公共溢出区

这种方法的基本思想是：将哈希表分为基本表和溢出表两部分，凡是和基本表发生冲突的元素，一律填入溢出表

二维数组

矩阵

code

此程序仅提供一个思路。

//Matrix.h
#ifndef _MATRIX_CLL_H__
#define _MATRIX_CLL_H__
#include "pch.h"


class Matrix{
private:
    int row, col;
    double ** data;
    void Initialize();//* 初始化矩阵
public:
    Matrix(int n);//* 初始化全0方阵
    Matrix(int r, int c);//* 初始化r行c列的全0矩阵
    Matrix(int r, int c, double val);//* 初始化r行c列的全val矩阵
    ~Matrix();
    
    Matrix& operator=(const Matrix&);//* 矩阵的复制
    Matrix& operator=(double *);//* 将数组的值传给矩阵
    Matrix& operator+=(const Matrix&);//* 矩阵加法
    Matrix& operator-=(const Matrix&);//* 矩阵减法
    Matrix& operator*=(const Matrix&);
    Matrix operator*(const Matrix & m) const;
    void Show()const;//* 矩阵显示
    static Matrix SwapMatris(const Matrix & m);//* 矩阵转置
    Matrix Inverse(Matrix);//* 矩阵求逆
    void SwapRow(int, int);//* 初等行变换

    double Point(int i, int j)const{ return this->data[i][j]; }//* 返回第i行，第j列的数字
    int GetRow()const{ return this->row; }
    int GetCol()const{ return this->col; }
    double Det();//* 计算矩阵对应的行列式
    static Matrix Eye(int);//*创造一个单位矩阵
    static Matrix Solve(const Matrix&, const Matrix&); //* 求解线性方程组Ax=b
    Matrix GaussianEliminate();//* 高斯消元法
    friend std::istream& operator>>(std::istream&, Matrix&);//* 实现矩阵输入
};

#endif

/*
pch.h中仅仅放入了需要使用到的头文件
*/
//Matrix.cpp
#include "Matrix.h"
#include "pch.h"

using std::endl;
using std::cout;
using std::istream;

const double EPS = 1e-10;

void Matrix::Initialize(){
    data = new double*[this->row];
    for(int i = 0; i < this->row; ++i){
        data[i] = new double[this->col];
    }
}
Matrix::Matrix(int n){
    this->row = this->col = n;
    Initialize();
    for(int i = 0; i < this->row; i++){
        for(int j = 0; j < this->col; j++){
            data[i][j] = 0;
        }
    }
}
Matrix::Matrix(int r, int c){
    this->row = r;
    this->col = c;
    Initialize();
    for(int i = 0; i < this->row; i++){
        for(int j = 0; j < this->col; j++){
            data[i][j] = 0;
        }
    }
}
Matrix::Matrix(int r, int c, double val){
    this->row = r;
    this->col = c;
    Initialize();
    for(int i = 0; i < this->row; i++){
        for(int j = 0; j < this->col; j++){
            data[i][j] = val;
        }
    }
}
Matrix::~Matrix(){
    for(int i = 0; i < this->row; ++i){
        delete [] data[i];
    }
    delete [] data;
}
Matrix& Matrix::operator=(const Matrix& m){
    if(this == &m){
        return *this;
    }
    if(this->row != m.row || this->col != m.col){
        for(int i = 0; i < this->row; ++i){
            delete [] data[i];
        }
        delete [] data;
        this->row = m.row;
        this->col = m.col;
        Initialize();
    }
    for(int i = 0; i < this->row; i++){
        for(int j = 0; j < this->col; j++){
            data[i][j] = m.data[i][j];
        }
    }
    return *this;
}
//* 将数组的值传递给矩阵（要求矩阵的大小已经被声明过）
Matrix& Matrix::operator=(double *a){
    for(int i = 0; i < this->row; i++){
        for(int j = 0; j < this->col; j++){
            data[i][j] = *(a+i*col+j);
        }
    }
    return *this;
}
//* +=操作
Matrix& Matrix::operator+=(const Matrix& m){
    for(int i = 0; i < this->row; i++){
        for(int j = 0; j col; j++){
            data[i][j] += m.data[i][j];
        }
    }
}
//* -=
Matrix& Matrix::operator-=(const Matrix& m){
    for(int i = 0; i < this->row; i++){
        for(int j = 0; j col; j++){
            data[i][j] -= m.data[i][j];
        }
    }
}
//* *=
Matrix& Matrix::operator*=(const Matrix& m){
    Matrix temp(row,col);//* 若C=AB,则矩阵C的行数等于A的列数，C的列数等于B的列数
    for(int i = 0; i < temp.row; i++){
        for(int j = 0; j < temp.col; j++){
            for(int k = 0; k < this->col; k++){
                temp.data[i][j] += (data[i][j] * m.data[i][j]);
            }
        }
    }
    *this = temp;
    return *this;
}
//* 实现矩阵乘法
Matrix Matrix::operator*(const Matrix& m) const {
    Matrix ba_M(row,col,0.0);
    for(int i = 0; i < row; i++){
        for(int j = 0; j < m.col; j++){
            for(int k = 0; k < col; k++){
                ba_M.data[i][j] += (data[i][j] * m.data[i][j]);
            }
        }
    }
    return ba_M;
}

//* 解方程组Ax=b
Matrix Matrix::Solve(const Matrix& A,const Matrix &b){
    //* 高斯消元实现Ax=b的方程求解
    for(int i=0; i < A.row; i++){
        if(A.data[i][i] == 0){
            cout<<"请重新输入"<= 0; i--){
        double sum = 0;
        for(int j = i + 1; j < x.row; j++){
            sum += A.data[i][j] * x.data[j][0];
        }
        x.data[i][0] = (b.data[i][0] - sum) / A.data[i][i];
        if(abs(x.data[i][0]) < EPS)     x.data[i][0] = 0;
    }
    return x;
}
//* 矩阵显示
void Matrix::Show()const{
    for(int i = 0; i < this->row; i++){
        for(int j = 0; j < this->col; j++){
            cout< EPS) && (abs(data[j][i]) > EPS)){
                    flag = true;//* 进行互换后，data[i][j]变为data[j][i],p[j][i]变为p[i][i]
                    //* 对矩阵进行行变换
                    double temp;
                    for(int k = 0; k < col; k++){
                        temp = data[i][k];
                        data[i][k] = data[j][k];
                        data[j][k] = temp;
                    }
                }
            }
            if(flag)    return 0;
        }
    }
    for(int i = 0; i < row; i++){
        for(int j = i + 1; j < row; j++){
            for(int k = i + 1; k < col; k++){
                data[j][k] -= data[i][k] * (data[j][i] * data[i][i]);
            }
        }
    }
    for(int i = 0; i < row; i++){
        ans *= data[i][i];
    }
    for(int i = 0; i < row; i++){
        for(int j = 0; j < col; j++){
            data[i][j] = back_up[i][j];
        }
    }
    return ans;
}

//* 矩阵求逆
Matrix Matrix::Inverse(Matrix A){
    if(A.row != A.col){
        std::cout << "只能求方阵的逆矩阵！"< EPS) && (abs(A.data[j][i]) > EPS)){
                    flag = true;
                    for(int k = 0; k < A.col; k++){
                        temp = A.data[i][k];
                        A.data[i][k] = A.data[j][k];
                        A.data[j][k] = temp;
                        temp = B.data[i][k];
                        B.data[i][k] = B.data[j][k];
                        B.data[j][k] = temp;
                    }
                }
            }
            if(!flag){
                std::cout <<"逆矩阵不存在"<= 1; i--){
        for(int j = i - 1; j >= 0; j--){
            temp = A.data[i][j];
            for(int k = 0; k < A.col; k++){
                A.data[j][k] -= A.data[i][k] * temp;
                B.data[j][k] -= B.data[i][k] * temp;
            }
        }
    }
    std::cout<<"算法检测，若可靠输出上三角矩阵"<= 0 ? Ab.data[k][j] : -1 * Ab.data[k][j];
                    if(cur_abs > max_val){
                        max_row = k;
                        max_val = cur_abs;
                    }
                }
                if(max_row != i){
                    Ab.SwapRow(max_row, i);
                    flag = true;
                }
                else{
                    j++;
                }
            }
        }
        if(flag){
            for(int t = i + 1; t < row; t++){
                for(int s = j + 1; s < col; s++){
                    Ab.data[t][s] = Ab.data[t][s] * (Ab.data[t][j] / Ab.data[i][j]);
                    if(abs(Ab.data[t][s]) < EPS){
                        Ab.data[t][s] = 0;
                    }
                }
                Ab.data[t][j] = 0;
            }
        }
        i++;j++;
    }
    return Ab;
}
//* 实现矩阵的输入 
istream& operator>>(istream& is, Matrix& m){
    for(int i = 0; i < m.row; i++){
        for(int j = 0; j < m.col; j++){
            is >> m.data[i][j];
        }
    }
    return is;
}

矩阵加速

https://blog.csdn.net/weixin_...

例1 斐波那契数列

题目链接：https://www.luogu.com.cn/prob...

题目大意

求第n项斐波那契数列摸1000000007的值，n在long long范围内

输入

一行，n

输出

f(n)%1000000007的值

样例输入

10
1
样例输出

55
1
分析

首先，直接递推肯定超时，可以观察如下两个式子

$$ f[n]=f[n-1]\times 1+f[n-2]\times 1 $$

$$ f[n-1]=f[n-1]\times 1+f[n-2]\times 0 $$

令

$$ 令A=\begin{bmatrix} 1 & 1\\1 &0 \end{bmatrix} $$

​

$$ 则A^{n} \times \begin{bmatrix} f(n-1)\\f(n-2) \end{bmatrix}=\begin{bmatrix} f(n) \\f(n-1) \end{bmatrix} $$

其中A^n 可以通过矩阵快速幂得到，这样就可以通过矩阵A来加速递推运算

Code

#include 
#include 
#include 
using namespace std;
typedef long long ll;
typedef vector vec;
typedef vector mat;

const ll mod = 1000000007;

inline mat mult (mat A, mat B) {
    int row = A.size(), col = B[0].size(), l = B.size();
    mat C(row, vec(col));
    for(int i = 0; i < row; i++)
        for(int j = 0; j < col; j++)
            for(int k = 0; k < l; k++)
                C[i][j] = C[i][j] % mod + A[i][k] * B[k][j] % mod;
    return C;
}

mat Power(mat &A, ll m) { //求快速幂
    ll n = A.size();
    mat res(n, vec(n));
    for(int i = 0; i < n; i++)
        res[i][i] = 1;
    while(m) {
        if(m & 1) res = mult(res, A);
        m >>= 1;
        A = mult(A, A);
    }
    return res;
}

int main () {
    ll n;
    mat a(2, vec(2));
    cin >> n;
    a[0][0] = 1, a[0][1] = 1; \\通过矩阵a来进行加速
    a[1][0] = 1, a[1][1] = 0;
    mat t = Power(a, n);
    cout << t[1][0] % mod << "\n";
    return 0;
}

例2 数列

题目链接：https://www.luogu.com.cn/prob...

题目大意：a[1] = a[2] = a[3] = 1,a[x] = a[x-3]+a[x-1] (x>3) 求a数列的第n项对1000000007取余的值。

输入：第一行一个整数T，表示询问个数。以下T行，每行一个正整数n。

输出：每行输出一个非负整数表示答案

输入Case：

​ 3

​ 6

​ 8

​ 10

输出Case：

​ 4

​ 9

​ 19

分析：同样使用矩阵加速递推，关键在于找到哪个矩阵来进行加速，由于这个递推公式跨度有3哥长度，所以可以写3个递推式：

$$ f[n] = 1 \times f[n-1] + 0 \times f[n-2] + 1 \times f[n-3] $$

$$ f[n-1] = 1 \times f[n-1] + 0 \times f[n-2] + 0 \times f[n-3] $$

$$ f[n-2] = 0 \times f[n-1] + 1 \times f[n-2] + 0 \times f[n-3] $$

同样提取系数，转换为矩阵乘法

$$ \begin{bmatrix} 1 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0 \end{bmatrix} \times \begin{bmatrix} f(n-1) \\f(n-2) \\f(n-3) \end{bmatrix} = \begin{bmatrix} f(n)\\f(n-1) \\f(n-2) \end{bmatrix} $$

$$ 令A=\begin{bmatrix} 1 & 0 & 1 \\ 1 & 0 & 0\\ 0 & 1 & 0 \end{bmatrix} $$

$$ \therefore A^{-3} \times \begin{bmatrix} f(3)\\f(2) \\f(1) \end{bmatrix}=\begin{bmatrix} f(n) \\ f(n-1) \\ f(n-2) \end{bmatrix} $$

$$ \therefore \begin{bmatrix} f(3)\\f(2) \\f(1) \end{bmatrix} = \begin{bmatrix} 1 \\1 \\1 \end{bmatrix} $$

#include 
#include 
#include 
#include 
#define ll long long
#define in(a) a = read();
using namespace std;
inline int read () {
    int f = 1, x = 0; char c = getchar();
    while(!isdigit(c)) {if(c == '-') f = -1; c = getchar();}
    while(isdigit(c)) {x = (x << 3) + (x << 1) + c - 48; c = getchar();}
    return f*x;
}

typedef vector vec;
typedef vector mat;
const ll mod = 1e9+7;

inline mat mul(mat A, mat B) {
    int row = A.size(), col = B[0].size(), l = B.size();
    mat C(row, vec(col));
    for(int i = 0; i < row; i++)
        for(int j = 0; j < col; j++)
            for(int k = 0; k < l; k++)
                C[i][j] = C[i][j] % mod + A[i][k] * B[k][j] % mod;
    return C;
}

inline mat powMod (mat A, int m) {
    int n = A.size();
    mat res(n, vec(n));
    for(int i = 0; i < n; i++)
        res[i][i] = 1;
    while(m) {
        if(m & 1) res = mul(res, A);
        m >>= 1;
        A = mul(A, A);
    }
    return res;
}

int main () {
    int T1, n;
    mat F(3, vec(3)), e(3, vec(1)); \\F矩阵用来加速，e表示初始的f(3)，f(2)，f(1)
    F[0][0] = 1, F[0][1] = 0, F[0][2] = 1;
    F[1][0] = 1, F[1][1] = 0, F[1][2] = 0;
    F[2][0] = 0, F[2][1] = 1, F[2][2] = 0;
    e[0][0] = 1, e[1][0] = 1, e[2][0] = 1;
    in(T1);
    while (T1 --) {
        in(n);
        n -= 3;
        if(n <= 0) printf("1\n");
        else {
            mat t = powMod(F, n);
            t = mul(t, e);
            printf("%lld\n", t[0][0] % mod); 
        } 
    }
    return 0;
}

例3 Blocks

题目链接：http://poj.org/problem?id=3734

题目大意：N个方块排成一列，有红、黄、绿、蓝四种颜色， 对方块染色，求当红色方块数和绿色方块数同为偶数个数的时候有多少种染色方案。结果对10007取余数。

输入：第一行一个T，表示测试数据数量（1 <= T <= 100）;接下来T行，每行一个n，表示方块的数量。（1 <= N <=10^9）

输出：对于每一个n，输出一个结果，每一个结果换一行

输入Case：

​ 2

​ 1

​ 2

输出Case：

​ 2

​ 6

分析：首先要找出递推关系式，然后才能用矩阵加速。

• 红绿都是偶数的方案数为Ai
• 红绿其中有一个偶数另一个是奇数的方案数为Bi
• 红绿都是奇数的方案数为Ci

$$ 考虑A_{i+1} = 2 \times A_{i} + B_{i} $$

(递推A的第 i+1块的时候，为保证红绿都为偶数。上一种红绿都是偶数的时候，新来一块可以选择黄蓝染色，同时还有上一种红绿只有一个为奇数，那么新来的一块只能染成这个奇数的颜色)

$$ 考虑B_{i},B_{i+1} = 2 \times A_{i} + 2 \times B_{i} + 2 \times C_{i} $$

（递推B的第 i+1块的时候，为了保证红绿只有一奇。上一种红绿都为偶数，新来一块可以选择红或者绿， 上一种红绿有一个为奇数，新来的一块可以染黄或者蓝色，如果上一种红绿都为奇数，新来的一块染红或者绿）

$$ 考虑C_{i}, C_{i+1} = B_{i} + 2 \times C_{i} $$

所以：

$$ A_{i+1}=2\times A_{i}+1\times B_{0}+0\times C_{i} $$

$$ B_{i+1}=2\times A_{i}+2\times B_{0}+2\times C_{i} $$

$$ C_{i+1}=0\times A_{i}+1\times B_{0}+2\times C_{i} $$

提取系数，转换矩阵乘法：

$$ \begin{bmatrix} 2 & 1 & 0\\ 2 & 2 & 2\\ 0 & 1 & 2 \end{bmatrix}\times \begin{bmatrix} A(n-1) \\ B(n-1) \\ C(n-1) \end{bmatrix}=\begin{bmatrix} A(n) \\ B(n) \\ C(n) \end{bmatrix} $$

$$ 令A =\begin{bmatrix} 2 & 1 & 0\\ 2 & 2 & 2\\ 0 & 1 & 2 \end{bmatrix} $$

$$ 则A_{n} =\begin{bmatrix} A(0)\\B(0)\\C(0) \end{bmatrix} $$

$$ \begin{bmatrix} A(0)\\B(0)\\C(0) \end{bmatrix}=\begin{bmatrix} 1\\0 \\0 \end{bmatrix} $$

Code

#include 
#include 
#include 
#include 
#define ll long long
#define in(a) a = read();
using namespace std;
inline int read () {
    int f = 1, x = 0; char c = getchar();
    while(!isdigit(c)) {if(c == '-') f = -1; c = getchar();}
    while(isdigit(c)) {x = (x << 3) + (x << 1) + c - 48; c = getchar();}
    return f*x;
}

typedef vector vec;
typedef vector mat;
const ll mod = 10007;

inline mat mul(mat A, mat B) {
    int row = A.size(), col = B[0].size(), l = B.size();
    mat C(row, vec(col));
    for(int i = 0; i < row; i++)
        for(int j = 0; j < col; j++)
            for(int k = 0; k < l; k++)
                C[i][j] = C[i][j] % mod + A[i][k] * B[k][j] % mod;
    return C;
}

inline mat powMod (mat A, int m) {
    int n = A.size();
    mat res(n, vec(n));
    for(int i = 0; i < n; i++)
        res[i][i] = 1;
    while(m) {
        if(m & 1) res = mul(res, A);
        m >>= 1;
        A = mul(A, A);
    }
    return res;
}

int main () {
    int T1, n;
    mat F(3, vec(3)), e(3, vec(1));
    F[0][0] = 2, F[0][1] = 1, F[0][2] = 0;
    F[1][0] = 2, F[1][1] = 2, F[1][2] = 2;
    F[2][0] = 0, F[2][1] = 1, F[2][2] = 2;
    e[0][0] = 1, e[1][0] = 0, e[2][0] = 0;
    in(T1);
    while (T1 --) {
        in(n);
        mat t = powMod(F, n);
        t = mul(t, e);
        printf("%lld\n", t[0][0] % mod); 
    }
    return 0;
}