算法导论习题解-第16章贪心算法
习题编号以第三版为准。
#16.1-3 失败的贪心算法
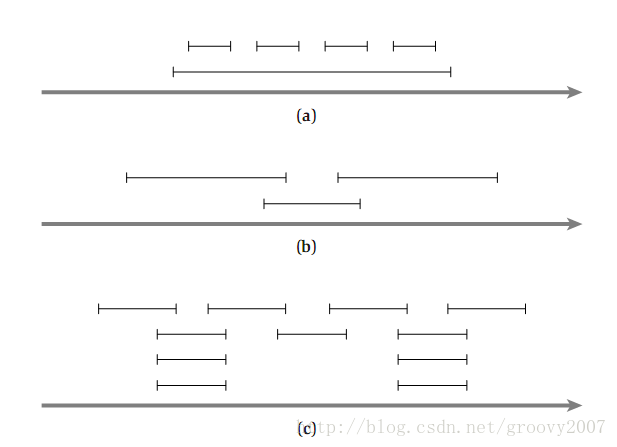
对于活动选择问题,并不是所有贪心方法都能得到最大兼容活动子集。请举例说明,每次选择时间最短者,或最早开始者,或重叠的活动数量最小者,均不能得到最优解。
解:如图所示。(a)最早开始 (b)时间最短 (c)重叠最少。图片来自Algorithm Design chapter 4.1 by Kleinberg
#16.1-4 区间图着色问题
使用最少的教室完成所有活动。用顶点表示活动,不兼容的活动之间有一条边。使用最少的颜色对顶点着色,使得任意边的两端颜色均不相同。(interval-graph color problem)
解:见Algorithm Design by Kleinberg 4.1节最后。思考:容易将活动问题转化为顶点着色问题,如何将顶点着色转化成活动问题?因为顶点上并没有时间顺序。
#16.1-5 带权重的活动选择问题
每个活动a[i]除了起止时间,还有一个价值v[i]。求价值最大的兼容活动子集,要求多项式时间。
解:参考课本中对原始问题的讨论,令S[i,j]表示在活动a[i]结束之后开始,且在a[j]开始之前结束的那些活动。考虑S[i,j]之中的一个活动a[k],则S[i,j] = S[i,k] + a[k] + S[k,j],动态规划可解。效率O(n * n)。
#16.2-6 线性时间的分数背包解法
解:见Instructor's Manual,关键思想:使用线性时间的中位数算法。
#16.2-7 最大乘积
取对数之后就变成了这样一个问题,两个数组a和b,各包含n个数,排列a和b中的元素,使得sum(a[i]*b[i])最大。
解:将a和b降序排列(或升序)。首先证明n=2的情况。然后假设a已经升序排列,b并没有升序排列,那么一定存在i
#16.3-6 用最少的位表示前缀码
假设有字母表C={0,1, ..., n-1}上的一个最优前缀码,希望用最少的二进制位传输此编码。说明如何仅用2n-1+nlg(n)位表示此前缀码。
解:使用2n-1位表示树的结构,内部节点用1表示,叶子节点用0。用nlg(n)位传送字母序列,每个字母占用lg(n)位。答案来自ustc answer。
#16.3-8 均匀分布时霍夫曼编码无效
假设一个文件由8位字符组成,所有256个字符的频率大致相同,最高频率也低于最低频率的2倍。证明此时霍夫曼编码并不优于定长编码。
解:证明此时的前缀树是一棵满二叉树。从最底层证起,最底层是两两配对的,且没有任何一对的频率超过另外一对的2倍。
#16-1 找零问题
O(nk)时间的找零算法,硬币面值为c1,c2, ...,ck,且c1=1,找零n分。
解:假设B(n)表示找零n美分需要的最少硬币数,硬币面值为c1,c2, ...,ck,则B(n)=1如果n等于某个ci,否则B(n) = 1 + min{ B(n-c1), B(n-c2), ..., B(n-ck) }
#16-5 离线缓存 furthest-in-future算法
解:见Algorithm Design by Kleinberg 4.3节,证明较为复杂。