【阅读笔记】Unsupervised Discovery of Interpretable Directions in the GAN Latent Space
论文名称:Unsupervised Discovery of Interpretable Directions in the GAN Latent Space
论文作者:Andrey V oynov, Artem Babenko
发行时间:Submitted on 10 Feb 2020, last revised 18 Feb 2020
论文地址:https://arxiv.org/abs/2002.03754
代码开源:https://github.com/anvoynov/GanLatentDiscovery
- 一. 概要
- 二. 实现方法
- 2.1. 方法阐述
- 2.2. 实现细节
- 2.2.1. 重构器 R R R 架构
- 2.2.2. 训练数据集的数据分布
- 2.2.3. K K K 的取值
- 2.2.4. A A A 的选择
- 三. 实验
- 3.1. 实验配置
- 3.1.1. 数据集和生成器模型
- 3.1.2. 优化器
- 3.1.3. 评估参数
- 3.1.3.1. RCA
- 3.1.3.2. DVN
- 3.2. MNIST
- 3.3. Anime Faces
- 3.4. Real Human Faces
- 3.5. ImageNet
- 3.1. 实验配置
一. 概要
本文首次提出使用无监督的方法来研究预先训练好的 GAN 中潜在空间的可解释性。这不同于其他如需要人为标签、预先训练的处理模型或某种形式的自我监督方法,无需花费较昂贵的代价就能有效地发现潜在编码的有效的可解释性移动方向。此外,提出的方法还能发现之前监督方法难以发现的方向:背景的去除。这说明可以用提出的方法来生成大规模的显著性实例检测的数据集,大大节省了人工力。
具体来说作者通过设置两组一定范围内的随机数来分别决定潜在编码的移动方向和移动幅度,然后用训练完毕的 GAN 模型中的生成器来生成原始潜在编码生成的图像和由沿着随机数确定的方向和位移移动了潜码生成的图像,然后通过一个重构组件得到预测的潜码移动方向和移动幅度。这样我们可以对其他图像的潜在编码进行预测到的移动,得到属性的操控。如 图1 所示,由无监督的方法在几个数据集上发现的可解释的方向。可见生成效果还是很不错的。

二. 实现方法
2.1. 方法阐述
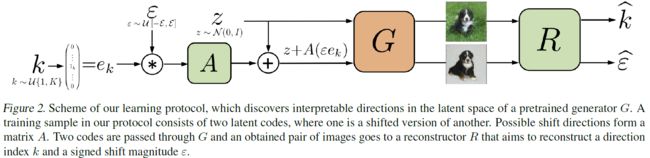
如 图2 所示,作者仅仅使用预训练好的 GAN 的生成器 G : z → I G:z\to I G:z→I 来将潜在编码生成图片(不使用其辨别器), 这个生成器是不可训练的,其参数在作者方法的处理阶段是固定的。同时作者还提出了两个可训练的组件 A A A 和 R R R:
-
数组 A ∈ R d × K A \in \mathbb{R}^{d\times K} A∈Rd×K,其中 d d d 等于 G G G 中潜在空间的维度, K K K 等于作者提出的方法试图解决的方向的数量(这取决于网络模型的选择和训练的数据集)。
z + A ( ε e k ) z+A(\varepsilon e_k) z+A(εek) -
重构器 R R R,其输入是图像对 ( G ( z ) , G ( z + A ( ε e k ) ) (G(z),G(z+A(\varepsilon e_k)) (G(z),G(z+A(εek)),其中 z ∼ N ( 0 , I ) z \sim \mathcal{N}(0,I) z∼N(0,I), z + A ( ε e k ) z+A(\varepsilon e_k) z+A(εek) 是移动了的潜在编码, e k e_k ek 表示轴对齐单位向量 ( 0 , ⋯ , 1 k , ⋯ , 0 ) (0,\cdots,1_k,\cdots,0) (0,⋯,1k,⋯,0), ε \varepsilon ε 是一个标量;输出是一个标量对 ( k ^ , ε ^ ) (\hat{k},\hat{\varepsilon}) (k^,ε^),其中 k ^ \hat{k} k^ 表示预测的方向的索引, ε ^ \hat{\varepsilon} ε^ 表示预测的移动幅度。 R R R 的目标是: 让潜码 z z z 往 A A A 的第 k k k 行决定的方向上移动 ε \varepsilon ε 实现了图像转换,然后 R R R 试图重现这种在潜在空间上的偏移。
R ( G ( z ) , G ( z + A ( ε e k ) ) = ( k ^ , ε ^ ) R(G(z),G(z+A(\varepsilon e_k))=(\hat{k},\hat{\varepsilon}) R(G(z),G(z+A(εek))=(k^,ε^)
作者选择的优化目标的表达式如下:
min A , R E z , k , ε L ( A , R ) = min A , R E z , k , ε [ L c l ( k , k ^ ) + λ L r ( ε , ε ^ ) ] \mathop{\min}\limits_{A,R}\mathop{\mathbb{E}}\limits_{z,k,\varepsilon}\mathcal{L}(A,R)=\mathop{\min}\limits_{A,R}\mathop{\mathbb{E}}\limits_{z,k,\varepsilon}[\mathcal{L}_{cl}(k,\hat{k})+\lambda\mathcal{L}_{r}(\varepsilon,\hat{\varepsilon})] A,Rminz,k,εEL(A,R)=A,Rminz,k,εE[Lcl(k,k^)+λLr(ε,ε^)]
上式中分别使用到了分类项 L c l ( ⋅ , ⋅ ) \mathcal{L}_{cl}(\cdot,\cdot) Lcl(⋅,⋅) 交叉熵损失和回归项 L r ( ⋅ , ⋅ ) \mathcal{L}_{r}(\cdot,\cdot) Lr(⋅,⋅) 平均绝对误差。这里的 λ \lambda λ 取值为 0.25 0.25 0.25。
- 对于分类项,作者希望通过该损失使得该方向更容易和其他方向区分开来,换句话说该特征的解耦性可以更强。
- 对于回归项,这可以使得潜在编码沿着某方向移动产生的图像具有连续性,不会突变。
2.2. 实现细节
作者在几个不同类别的数据集下(手写数据集MNIST、动漫人脸数据集AnimeFaces、真实人脸数据集CelebA-HQ和自然景观数据集ImageNet)进行了本文方法的实验。
2.2.1. 重构器 R R R 架构
对于重构模型 R R R:
- 对于
MNIST和AnimeFaces数据集,使用LeNet骨干网络 - 对于
ImageNet和CelebA-HQ数据集,使用ResNet-18作为骨干网络
在所有实验中,除能 MNIST 的输入通道为 2 2 2 外,其他数据集的输入通道都为 6 6 6,因为输入 R R R 的是图像对。作者还往其中加上了两个单独的 heads 分别用于预测方向索引和位移幅度。
2.2.2. 训练数据集的数据分布
- z ∈ N ( 0 , I ) z \in \mathcal{N}(0,I) z∈N(0,I)
- k ∈ U { 1 , K } k \in \mathcal{U}\left \{ 1,K \right \} k∈U{1,K}
- ε ∈ U [ − 6 , 6 ] \varepsilon \in \mathcal{U}[-6,6] ε∈U[−6,6]
由于当 ε → 0 \varepsilon \to 0 ε→0 时,由于位移幅度过小,几乎不会对位移后的生成图像造成影响,所以在实验中作者对 ε \varepsilon ε 的取值做了以下约束:
ε = s i g n ( ε ) ⋅ max ( ∣ ε ∣ , 0.5 ) \varepsilon = {\rm sign}(\varepsilon)\cdot \max(|\varepsilon|,0.5) ε=sign(ε)⋅max(∣ε∣,0.5)
2.2.3. K K K 的取值
通常 K K K 的取值要等于潜在空间的维度(Spectral Norm GAN维度是 128 128 128,BigGAN维度是 120 120 120,ProgGAN维度是 512 512 512)。但是由于模型的限制和数据集的限制,需要有一定的取舍,具体取值如下所示:
- 用
Spectral Norm GAN处理MNIST数据集时 K = 64 K=64 K=64,因为若取值为 128 128 128 时模型很难讲较简单的数字图形弄出过多的不同的可解释性方向。 - 用
Spectral Norm GAN处理AnimeFaces数据集时 K = 128 K=128 K=128。 - 用
BigGAN处理ImageNet数据集时 K = 120 K=120 K=120。 - 用
ProgGAN处理CelebA-HQ数据集时 K = 200 K=200 K=200,因为若取值为 512 512 512 时,作者提出的方法很重构出合理的评价指标值。
2.2.4. A A A 的选择
在实验中作者用到了两种 A A A :
- A is a linear operator with all matrix columns having a unit length:让矩阵的所有列都是单位长度,通过让每列除以其对应长度得到。
- A is a linear operator with orthonormal matrix columns:让矩阵的列都是正交的,即通过斜对称矩阵 S S S ( S T = − S S^T=-S ST=−S)来参数化 A A A。
在实验中观察到,这两种 A A A 的效果都挺好,并且能发现一些相似的可解释性方向。通常更常使用单位向量的列的 A A A,因为其能发现更多的方向。但在某些数据集中,第二种 A A A 能发现一些更有趣的细节。
三. 实验
3.1. 实验配置
3.1.1. 数据集和生成器模型
MNIST,包含 32 × 32 32\times32 32×32 大小的图像,使用 3 3 3 个残差块的ResNet-like生成器的Spectral Norm GAN。AnimeFaces,包含 64 × 64 64\times64 64×64 大小的图像,使用 4 4 4 个残差块的ResNet-like生成器的Spectral Norm GAN。CelebA-HQ,包含 1024 × 1024 1024\times1024 1024×1024 大小的图像,使用预训练好的ProGAN生成器 online available。ImageNet,包含 128 × 128 128\times128 128×128 大小的图像,使用在ILSVRC数据集上预训练好的BigGAN生成器 online available。
3.1.2. 优化器
全部使用 Adam 优化器,固定学习率 0.0001 0.0001 0.0001,除了 ProGAN 使用梯度回传训练了 1 0 5 10^5 105 次外,其他都是 2 × 1 0 5 2\times10^5 2×105 次。在 MNIST 上的 batch=128,在 AnimeFaces 上的 batch=128,在 CelebA-HQ 上的 batch=10,在 ImageNet 上的 batch=32。
3.1.3. 评估参数
- RCA越高,该方向表示的特征和其他特征的解耦度越低,区分性更高。
- DVN越高,该方向决定的特征的可解释性越强。
3.1.3.1. RCA
RCA,Reconstructor Classification Accuracy,重构分类准确率。作为重构模型中的分类头,其处理的是一个多分类问题。因此,RCA越高,该方向表示的特征和其他特征的解耦度越低,区分性更高。此外,RCA的计算上还能将我们方法和随机得到的方法(A:Random Matrix)或沿坐标轴移动的方法(A:Identity Matrix)进行结果比对。
3.1.3.2. DVN
DVN,Direction Variation Naturalness,方向变化的自然度。表示在潜空间中让隐编码沿着特定方向变化其生成的图像的自然性。按照常识,自然性应该是沿着某个方向移动生成的图像和真实图像之间的变化因子应该是相同的,于是,作者通过使用如下方法达到自然性的计算:
- 将我们重构模型 R R R 得到的方向和位移组成的方向向量记为 h F h_{\mathcal{F}} hF,便可构建一个适用于二分类任务的伪标签数据集 D F = { ( G ( z ± h F ) , ± 1 ) } D_{\mathcal{F}}=\left \{ (G(z \pm h_{\mathcal{F}}),\pm1) \right \} DF={(G(z±hF),±1)}。
- 使用
LeNet对该数据集进行训练,得到一个二分类模型 M F : G ( z ) → { − 1 , 1 } M_{\mathcal{F}}:G(z)\to \left \{ -1,1 \right \} MF:G(z)→{−1,1}。 - 再利用训练好的 M F M_{\mathcal{F}} MF 对对应的真实图像集 D D D 引入伪标签数据集 D F r e a l = { ( I , M F ( I ) ) , I ∈ D } D_{\mathcal{F}}^{real}=\left \{ (I,M_{\mathcal{F}}(I)),I \in D \right \} DFreal={(I,MF(I)),I∈D}。
- 重新让这个二分类模型 M F M_{\mathcal{F}} MF 在 D F r e a l D_{\mathcal{F}}^{real} DFreal 数据集上重新训练,然后用新的 M F M_{\mathcal{F}} MF 对 D F D_{\mathcal{F}} DF 进行测试,得到准确性,即 DVN。
3.2. MNIST

图6是提出方法在 MNIST 上的定性分析,可见图像伴随着潜在编码沿着学习到的方向移动的效果还是很好的。
为了衡量方法的解耦能力,作者设计了如下实验:
- 固定 k k k 和 z z z,从训练次数上分别从 0 ∼ 1 0 5 0\sim10^5 0∼105 均分成 5 5 5 份取对应步数上的预测方向。即 A : A s t e p = 0 , ⋯ , A s t e p = 1 0 5 A:A_{step=0},\cdots,A_{step=10^5} A:Astep=0,⋯,Astep=105。
- A s t e p = 0 A_{step=0} Astep=0:做恒等变化
- A s t e p = 1 0 5 A_{step=10^5} Astep=105:最终的预测矩阵
实验结果如 图7 所示,可见,随着训练步数逐渐接近 1 0 5 10^5 105,往该方向的移动不再改变数字类型,仅仅改变数字的粗细,充分表明我们将数字类型和数字粗细这俩特征解耦了。

3.3. Anime Faces
就是在这个数据集上发现将 A A A 的各列正交可增强方向的多样性。 但不提倡用这个方法到所有数据集上,因为未必都能取得这样的效果(作者对MNIST、CelebA上实验效果没这样好)。实验结果如 图8 所示。
3.4. Real Human Faces
图9 即为实验结果,这些方向为图像的处理提供了有用信息。
3.5. ImageNet
图10 便是提出的方法发现的一些方向。值得一提的是,上图中的 背景模糊 和 背景消除 这俩方向可为构建显著性实例分割任务轻松构建大规模的训练数据集。而这俩方向便是正交列矩阵 A A A 的功劳。