吴恩达机器学习笔记整理(Week1-Week5)
吴恩达机器学习笔记整理
- 1. Week1
- 1.1 什么是机器学习(What is Machine Learning)
- 1.2机器学习算法分类
- 1.3 单变量线性回归(Linear Regression with One Variable)
- 1.4 梯度下降(Gradient Descent)
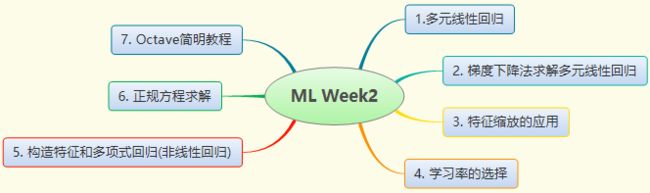
- 2. Week2
- 2.1 多变量线性回归(Linear Regression with Multiple Variables)
- 2.1.1 多变量对应的新记号
- 2.1.2 多变量梯度下降(Gradient Descent for Multiple Variables)
- 2.1.3 梯度下降实践1-特征值缩放(Gradient Descent in Practice I - Feature Scaling)
- 2.1.4 梯度下降实践2-学习速率(Gradient Descent in Practice II - Learning Rate)
- 2.1.5 正规方程(Normal Equation)
- 2.1.6 不可逆性正规方程(Normal Equation Noninvertibility)
- 2.2 Octave/Matlab 简明教程
- 2.2.1 Octave/Matlab Tutorial 基本操作
- 2.2.2 Octave/Matlab Tutorial 计算数据
- 2.2.3 Octave/Matlab Tutorial 数据绘制
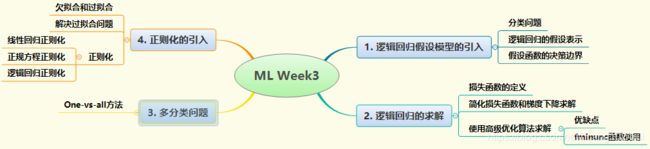
- 3.Week3
- 3.1 逻辑回归(Logistic Regression)
- 3.1.1 假设函数表示(Hypothesis Representation)
- 3.1.2 决策边界(Decision Boundary)
- 3.1.3 代价函数(Cost Function)
- 3.1.4 简化的成本函数和梯度下降(Simplified Cost Function and Gradient Descent)
- 3.1.5 进阶优化(Advanced Optimization)
- 3.1.6 多类别分类: 一对多(Multiclass Classification: One-vs-all)
- 3.2 正则化(Regularization)
- 3.2.1 过拟合问题(The Problem of Overfitting)
- 3.2.2 代价函数(Cost Function)
- 3.2.3 线性回归正则化(Regularized Linear Regression)
- 3.2.4 逻辑回归正则化(Regularized Logistic Regression)
- 4. Week 4(神经网络:表达(Neural Networks: Representation))
- 4.1 非线性假设(Non-linear Hypotheses)
- 4.2 神经网络和大脑(Neurons and the Brain)
- 4.3 模型表示1(Model Representation I)
- 4.4 模型表示2(Model Representation II)
- 4.5 例子和直观理解1(Examples and Intuitions I)
- 4.6 例子和直观理解2(Examples and Intuitions II)
- 4.7 多类别分类(Multiclass Classification)
- 5. Week 5(神经网络的学习(Neural Networks: Learning))
- 5.1 代价函数
- 5.2 反向传播算法
- 5.3 反向传播算法的直观理解
- 5.3.1 神经网络中代价函数求导的推导过程-1:
- 5.3.2 神经网络中代价函数求导的推导过程-2:
- 5.4 实现注意点: 参数展开(Implementation Note: Unrolling Parameters)
- 5.5 梯度检验(Gradient Checking)
- 5.6 随机初始化(Random Initialization)
- 5.7 综合起来(Putting It Together)
有道云笔记上的笔记太乱,花点时间把笔记整理过来,顺道自己重新看看~
1. Week1
1.1 什么是机器学习(What is Machine Learning)
机器学习定义 这里主要有两种定义:
-
Arthur Samuel (1959). Machine Learning: Field of study that gives computers the ability to learn without being explicitly programmed.
这个定义有点不正式但提出的时间最早,来自于一个懂得计算机编程的下棋菜鸟。他编写了一个程序,但没有显式地编程每一步该怎么走,而是让计算机自己和自己对弈,并不断地计算布局的好坏,来判断什么情况下获胜的概率高,从而积累经验,好似学习,最后,这个计算机程序成为了一个比他自己还厉害的棋手。
-
Tom Mitchell (1998) Well-posed Learning Problem: A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.
Tom Mitchell 的定义更为现代和正式。在过滤垃圾邮件这个例子中,电子邮件系统会根据用户对电子邮件的标记(是/不是垃圾邮件)不断学习,从而提升过滤垃圾邮件的准确率,定义中的三个字母分别代表:
- T(Task): 过滤垃圾邮件任务。
- P(Performance): 电子邮件系统过滤垃圾邮件的准确率。
- E(Experience): 用户对电子邮件的标记。
1.2机器学习算法分类
主要有两种机器学习的算法分类
-
监督学习
监督学习,即为教计算机如何去完成预测任务(有反馈),预先给一定数据量的输入和对应的结果即训练集,建模拟合,最后让计算机预测未知数据的结果。
监督学习一般有两种:
1.回归问题(Regression):回归问题即为预测一系列的连续值。
2.分类问题(Classification)分类问题即为预测一系列的离散值。即根据数据预测被预测对象属于哪个分类。 -
无监督学习
相对于监督学习,训练集不会有人为标注的结果(无反馈),我们不会给出结果或无法得知训练集的结果是什么样,而是单纯由计算机通过无监督学习算法自行分析,从而“得出结果”。计算机可能会把特定的数据集归为几个不同的簇,故叫做聚类算法。
无监督学习一般分为两种:
1.聚类(Clustering):新闻聚合、DNA 个体聚类、天文数据分析、市场细分、社交网络分析
2.非聚类(Non-clustering):鸡尾酒问题
两者的区别为是否需要人工参与数据结果的标注。这两部分的内容占比很大,并且很重要,掌握好了可以在以后的应用中节省大把大把的时间~
还有一些算法也属于机器学习领域,诸如:
- 半监督学习: 介于监督学习于无监督学习之间
- 推荐算法: 没错,就是那些个买完某商品后还推荐同款的某购物网站所用的算法。
- 强化学习: 通过观察来学习如何做出动作,每个动作都会对环境有所影响,而环境的反馈又可以引导该学习算法。
- 迁移学习
1.3 单变量线性回归(Linear Regression with One Variable)
-
问题解决模型

`其中 h ( x ) h(x) h(x)代表结果函数,也称为 假设(hypothesis) 。假设函数根据输入(房屋的面积),给出预测结果输出(房屋的价格),即是一个 X → Y X \to Y X→Y的映射。 -
代价函数(Cost Function)
李航《统计学习方法》一书中,损失函数与代价函数两者为同一概念,未作细分区别,全书没有和《深度学习》一书一样混用,而是统一使用损失函数来指代这类类似概念。
吴恩达(Andrew Ng)老师在其公开课中对两者做了细分。如果要听他的课做作业,不细分这两个概念是会被打小手扣分的!这也可能是因为老师发现了业内混用的乱象,想要治一治吧。
- 损失函数(Loss/Error Function): 计算单个样本的误差( h θ ( x j ( i ) ) − y j ( i ) h_{\theta}\left(x_j^{(i)}\right)-y_j^{(i)} hθ(xj(i))−yj(i))。
- 代价函数(Cost Function): 计算整个训练集所有损失函数之和的平均值( ∑ i = 0 m ( h θ ( x ( i ) ) − y ( i ) ) \sum_{i=0}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) ∑i=0m(hθ(x(i))−y(i))).
- 目标函数(Objective function):字面一些,就是有某个(最优化)目标的函数,比如最优化这个目的。个人理解,目标函数是一个大类,包含损失函数、代价函数;损失函数、代价函数,属于目标函数。
机器学习中的目标函数、损失函数、代价函数有什么区别?- 知乎
1.4 梯度下降(Gradient Descent)
-
根据上节视频,列出如下定义:
- 假设函数(Hypothesis): h θ ( x ) = θ 0 + θ 1 x h_\theta(x) = \theta_0 + \theta_1 x hθ(x)=θ0+θ1x
- 参数(Parameters): θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1
- 代价函数(Cost Function): J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 0 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=0}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^2 J(θ0,θ1)=2m1∑i=0m(hθ(x(i))−y(i))2
- 目标(Goal): min θ 0 , θ 1 J ( θ 0 , θ 1 ) \min_{\theta_0,\theta_1} J(\theta_0,\theta_1) minθ0,θ1J(θ0,θ1)
-
梯度下降公式:
repeat until convergence:{
θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) \theta_{j}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right) θj:=θj−α∂θj∂J(θ0,θ1)
}其中:
θ j \theta_{j} θj: 第j个特征参数
: = := :=: 赋值操作符
α \alpha α: 学习速率(learning rate), α > 0 \alpha>0 α>0
∂ ∂ θ j J ( θ 0 , θ 1 ) \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right) ∂θj∂J(θ0,θ1): J ( θ 0 , θ 1 ) J\left(\theta_{0},\theta_{1}\right) J(θ0,θ1) 的偏导

-
学习速率 α \alpha α
需要选取一个合适的值才能使得梯度下降算法运行良好:- 学习速率过小:收敛的太慢,需要更多次的迭代。
- 学习速率过大:可能越过最低点,甚至导致无法收敛。
- 学习速率只需选定即可,不需要在运行梯度下降算法的时候进行动态改变,随着斜率越来越接近于0,代价函数的变化幅度会越来越小,直到收敛到局部极小值。
2. Week2
2.1 多变量线性回归(Linear Regression with Multiple Variables)
2.1.1 多变量对应的新记号
-
数据的新记号
- n n n: 特征的总数
- x ( i ) {x}^{\left( i \right)} x(i): 代表样本矩阵中第 i i i 行,也就是第 i i i 个训练实例。
- x j ( i ) {x}_{j}^{\left( i \right)} xj(i): 代表样本矩阵中第 i i i 行的第 j j j 列,也就是第 i i i 个训练实例的第 j j j 个特征。
-
假设函数的新记号
多变量假设函数 h h h 表示为: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}} hθ(x)=θ0+θ1x1+θ2x2+...+θnxn
h θ ( x ) = [ θ 0 θ 1 … θ n ] [ x 0 x 1 ⋮ x n ] = θ T x h_{\theta}(x)=\left[\begin{array}{ccc}\theta_{0} & \theta_{1} \ldots \theta_{n}\end{array}\right]\left[\begin{array}{c}x_{0} \\ x_{1} \\ \vdots \\ x_{n}\end{array}\right]=\theta^{T} x hθ(x)=[θ0θ1…θn]⎣⎢⎢⎢⎡x0x1⋮xn⎦⎥⎥⎥⎤=θTxθ T \theta^T θT: θ \theta θ 矩阵的转置
x x x: 某个样本的特征向量, n + 1 n+1 n+1 维特征量向量
x 0 x_0 x0: 为了计算方便我们会假设 x 0 ( i ) = 1 x_0^{(i)} = 1 x0(i)=1
2.1.2 多变量梯度下降(Gradient Descent for Multiple Variables)
多变量代价函数类似于单变量代价函数,
即 J ( θ 0 , θ 1 . . . θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( {\theta_{0}},{\theta_{1}}...{\theta_{n}} \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( h_{\theta} \left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}} J(θ0,θ1...θn)=2m1i=1∑m(hθ(x(i))−y(i))2 ,其中 h θ ( x ) = θ T x h_\theta\left(x\right)= \theta^T x hθ(x)=θTx。
前文提到梯度下降对于最小化代价函数的通用性,则多变量梯度下降公式即
repeat until convergence: { θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 … θ n ) } \theta_{j}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1} \ldots \theta_{n}\right)\} θj:=θj−α∂θj∂J(θ0,θ1…θn)}
解出偏导方程:
repeat until convergence: {
θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) \theta_{j}:=\theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{j}^{(i)} θj:=θj−αm1∑i=1m(hθ(x(i))−y(i))⋅xj(i) for j : = 0 , 1 … n \mathrm{j}:=0,1 \ldots \mathrm{n} j:=0,1…n
}
可展开为:
repeat until convergence: {
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 0 ( i ) \theta_{0}:=\theta_{0}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{0}^{(i)} θ0:=θ0−αm1∑i=1m(hθ(x(i))−y(i))⋅x0(i)
θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 1 ( i ) \theta_{1}:=\theta_{1}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{1}^{(i)} θ1:=θ1−αm1∑i=1m(hθ(x(i))−y(i))⋅x1(i)
θ 2 : = θ 2 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x 2 ( i ) \theta_{2}:=\theta_{2}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{2}^{(i)} θ2:=θ2−αm1∑i=1m(hθ(x(i))−y(i))⋅x2(i)
θ n : = θ n − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x n ( i ) \theta_{n}:=\theta_{n}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{n}^{(i)} θn:=θn−αm1∑i=1m(hθ(x(i))−y(i))⋅xn(i)
}
当然,同单变量梯度下降一样,计算时需要 同 时 更 新 \color{red}同时更新 同时更新所有参数。
h θ ( x ) = θ T x h_\theta\left(x\right)= \theta^T x hθ(x)=θTx,则得到同时更新参数的向量化(Vectorization)实现:
θ = θ − α 1 m ( X T ( X θ − y ) ) \theta = \theta - \alpha \frac{1}{m}(X^T(X\theta-y)) θ=θ−αm1(XT(Xθ−y))
X X X: 训练集数据, m × ( n + 1 ) m\times(n+1) m×(n+1) 维矩阵(包含基本特征 x 0 = 1 x_0=1 x0=1)
2.1.3 梯度下降实践1-特征值缩放(Gradient Descent in Practice I - Feature Scaling)
在应用梯度下降算法实践时,由于各特征值的范围不一,可能会影响代价函数收敛速度。
为了优化梯度下降的收敛速度,采用特征缩放的技巧,使各特征值的范围尽量一致。
除了以上图人工选择并除以一个参数的方式,均值归一化(Mean normalization) 方法更为便捷,可采用它来对所有特征值统一缩放:
x i : = x i − a v e r a g e ( x ) m a x i m u m ( x ) − m i n i m u m ( x ) x_i:=\frac{x_i-average(x)}{maximum(x)-minimum(x)} xi:=maximum(x)−minimum(x)xi−average(x), 使得 x i ∈ ( − 1 , 1 ) x_i \in (-1,1) xi∈(−1,1)
对于特征的范围,并不一定需要使得 − 1 ⩽ x ⩽ 1 -1 \leqslant x \leqslant 1 −1⩽x⩽1,类似于 1 ⩽ x ⩽ 3 1\leqslant x \leqslant 3 1⩽x⩽3 等也是可取的,而诸如 − 100 ⩽ x ⩽ 100 -100 \leqslant x \leqslant 100 −100⩽x⩽100, − 0.00001 ⩽ x ⩽ 0.00001 -0.00001 \leqslant x \leqslant 0.00001 −0.00001⩽x⩽0.00001,就显得过大/过小了。
另外注意,一旦采用特征缩放,我们就需对所有的输入采用特征缩放,包括训练集、测试集、预测输入等。
2.1.4 梯度下降实践2-学习速率(Gradient Descent in Practice II - Learning Rate)
通常,有两种方法来确定函数是否收敛
- 多次迭代收敛法
- 无法确定需要多少次迭代
- 较易绘制关于迭代次数的图像
- 根据图像易预测所需的迭代次数
- 自动化测试收敛法(比较阈值)
- 不易选取阈值
- 代价函数近乎直线时无法确定收敛情况
对于梯度下降,一般采用多次迭代收敛法来得出最小化代价函数的参数值,自动化测试收敛法(如设定 J ( θ ) < 10 − 3 J\left(\theta\right) < {10}^{-3} J(θ)<10−3 时判定收敛)则几乎不会被使用。
我们可以通过绘制代价函数关于迭代次数的图像,可视化梯度下降的执行过程,借助直观的图形来发现代价函数趋向于多少时能趋于收敛,依据图像变化情况,确定诸如学习速率的取值,迭代次数的大小等问题。
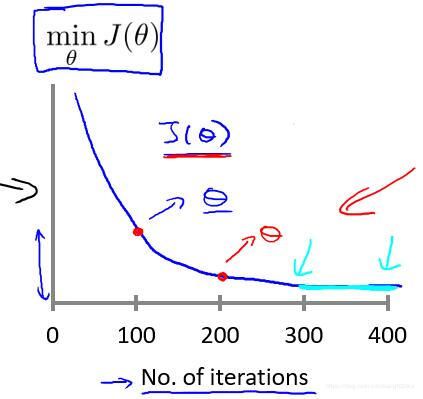
对于学习速率 α \alpha α,一般上图展现的为适中情况,
- α \alpha α 过大,代价函数无法收敛,会出现屁股型,即:一下上,一下下;
- α \alpha α 过小,代价函数收敛的太慢。当然, α \alpha α 足够小时,代价函数在每轮迭代后一定会减少。
通过不断改变 α \alpha α 值,绘制并观察图像,并以此来确定合适的学习速率。 尝试时可取 α \alpha α 如 … 0 , 001 , 0.003 , 0.01 , 0.03 , 0.1 , … \dots\;0,001,\;0.003,\;0.01,\;0.03,\;0.1,\;\dots …0,001,0.003,0.01,0.03,0.1,…
2.1.5 正规方程(Normal Equation)
-
正规方程的应用
对于一些线性回归问题来说,正规方程法给出了一个更好的解决问题的方式。正规方程法,即令 ∂ ∂ θ j J ( θ j ) = 0 \frac{\partial}{\partial{\theta_{j}}}J\left( {\theta_{j}} \right)=0 ∂θj∂J(θj)=0 ,通过解析函数的方式直接计算得出参数向量的值 θ = ( X T X ) − 1 X T y \theta ={{\left( {X^T}X \right)}^{-1}}{X^{T}}y θ=(XTX)−1XTy ,Octave/Matlab 代码:
theta = inv(X'*X)*X'*y。X − 1 {X}^{-1} X−1: 矩阵 X X X 的逆,在 Octave 中,
inv函数用于计算矩阵的逆,类似的还有pinv函数。
X': 在 Octave 中表示矩阵 X 的转置,即 X T X^T XT下表列出了正规方程法与梯度下降算法的对比
| 条件 | 梯度下降 | 正规方程 |
|---|---|---|
| 是否需要选取 α \alpha α | 需要 | 不需要 |
| 是否需要迭代运算 | 需要 | 不需要 |
| 特征量大[1]时 | 适用, O ( k n 2 ) O\left(kn^2\right) O(kn2) | 不适用, ( X T X ) − 1 (X^TX)^{-1} (XTX)−1 复杂度 O ( n 3 ) O\left( {{n}^{3}} \right) O(n3) |
| 适用范围[2] | 各类模型 | 只适用线性模型,且矩阵需可逆 |
[1]: 一般来说,当 n n n 超过 10000 时,对于正规方程而言,特征量较大。
[2]: 梯度下降算法的普适性好,而对于特定的线性回归模型,正规方程是很好的替代品。
-
正规方程法的推导过程:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = 1 2 m ∣ ∣ X θ − y ∣ ∣ 2 = 1 2 m ( X θ − y ) T ( X θ − y ) \begin{aligned} & J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {h_{\theta}}\left( {x^{(i)}} \right)-{y^{(i)}} \right)}^{2}}}\newline \; & =\frac{1}{2m}||X\theta-y||^2 \newline \; & =\frac{1}{2m}(X\theta-y)^T(X\theta-y) &\newline \end{aligned} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2=2m1∣∣Xθ−y∣∣2=2m1(Xθ−y)T(Xθ−y)展开上式可得
J ( θ ) = 1 2 m ( θ T X T X θ − θ T X T y − y T X θ + y T y ) J(\theta )= \frac{1}{2m}\left( {{\theta }^{T}}{{X}^{T}}X\theta -{{\theta}^{T}}{{X}^{T}}y-{{y}^{T}}X\theta + {{y}^{T}}y \right) J(θ)=2m1(θTXTXθ−θTXTy−yTXθ+yTy)
注意到 θ T X T y {{\theta}^{T}}{{X}^{T}}y θTXTy 与 y T X θ {{y}^{T}}X\theta yTXθ 都为标量,实际上是等价的,则
J ( θ ) = 1 2 m [ X T X θ − 2 θ T X T y + y T y ] J(\theta) = \frac{1}{2m}[X^TX\theta-2\theta^TX^Ty+y^Ty] J(θ)=2m1[XTXθ−2θTXTy+yTy]
接下来对 J ( θ ) J(\theta ) J(θ) 求偏导,根据矩阵的求导法则:
d X T A X d X = ( A + A T ) X \frac{dX^TAX}{dX}=(A+A^\mathrm{T})X dXdXTAX=(A+AT)X
d X T A d X = A \frac{dX^TA}{dX}={A} dXdXTA=A
所以有:
∂ J ( θ ) ∂ θ = 1 2 m ( 2 X T X θ − 2 X T y ) = X T X θ − X T y \frac{\partial J\left( \theta \right)}{\partial \theta }=\frac{1}{2m}\left(2{{X}^{T}}X\theta -2{{X}^{T}}y \right)={{X}^{T}}X\theta -{{X}^{T}}y ∂θ∂J(θ)=2m1(2XTXθ−2XTy)=XTXθ−XTy
令 ∂ J ( θ ) ∂ θ = 0 \frac{\partial J\left( \theta \right)}{\partial \theta }=0 ∂θ∂J(θ)=0, 则有
θ = ( X T X ) − 1 X T y \theta ={{\left( {X^{T}}X \right)}^{-1}}{X^{T}}y θ=(XTX)−1XTy
2.1.6 不可逆性正规方程(Normal Equation Noninvertibility)
正规方程无法应用于不可逆的矩阵,发生这种问题的概率很小,通常由于
-
特征之间线性相关
比如同时包含英寸的尺寸和米为单位的尺寸两个特征,它们是线性相关的
即 x 1 = x 2 ∗ ( 3.28 ) 2 {x_{1}}={x_{2}}*{{\left( 3.28 \right)}^{2}} x1=x2∗(3.28)2。
-
特征数量大于训练集的数量 ( m ⩽ n ) \left(m \leqslant n \right) (m⩽n)。
如果发现 X T X X^TX XTX 的结果不可逆,可尝试:
- 减少多余/重复特征
- 增加训练集数量
- 使用正则化(后文)
对于这类不可逆的矩阵,我们称之为奇异矩阵或退化矩阵。
这种情况下,如果还想使用正规方程法,在Octave中,可以选用 pinv 函数,pinv 区别于 inv,pinv 函数被称为伪逆函数,在矩阵不可逆的时候,使用这个函数仍可正确地计算出 θ \theta θ 的值。
2.2 Octave/Matlab 简明教程
2.2.1 Octave/Matlab Tutorial 基本操作
rand数值介于0、1之间;randn均值0方差1的正态分布。- 用
hist命令绘制直方图;用eye绘制单位矩阵。 - 长度(
length,size),查看(who,whos,pwd),加载(load)和存储(save,clear)。 A([1 3],;)矩阵A中第一行和第三行。
2.2.2 Octave/Matlab Tutorial 计算数据
A*B表示矩阵的乘法;A.*B表示A的每一个元素与矩阵B中的对应元素相乘(类似A./B)。- 转置:
A';伪逆pinv(A);magic函数(返回一个:所有的行和列和对角线加起来都等于相同的矩阵)。 prod(A)表示所有矩阵元素乘积。floor(A)元素向下取整,ceil(A)元素向上取整。max(A,[],1)/max(A,[],2):返回每一列/每一行的最大值。A(:)让矩阵变成列向量;sum(A,1)A矩阵的每一列求和;sum(sum(A.*eye(9)))表示求对角线的和。flipud(A)矩阵垂直翻转。
2.2.3 Octave/Matlab Tutorial 数据绘制
hold on表示停留以前的图,再以前的图上画新图。legend()表示显示图像的标志;axis()改变轴变化范围。clf清除一幅图像;imgesc(A);colorbar;colormap gray。- 特征缩放:
repmat()用于重新建立想要的重复矩阵;标准差std;diag()和mean()建立对角矩阵。
3.Week3
3.1 逻辑回归(Logistic Regression)
区别于线性回归算法,逻辑回归算法是一个分类算法,其输出值永远在 0 到 1 之间,即 h θ ( x ) ∈ ( 0 , 1 ) h_\theta(x) \in (0,1) hθ(x)∈(0,1)。
3.1.1 假设函数表示(Hypothesis Representation)
为了使 h θ ( x ) ∈ ( 0 , 1 ) h_\theta(x) \in \left(0, 1\right) hθ(x)∈(0,1),引入逻辑回归模型,定义假设函数
h θ ( x ) = g ( z ) = g ( θ T x ) h_\theta \left( x \right)=g(z)=g\left(\theta^{T}x \right) hθ(x)=g(z)=g(θTx)
- 对比线性回归函数 h θ ( x ) = θ T x h_\theta \left( x \right)=\theta^{T}x hθ(x)=θTx, g g g 表示逻辑函数([logistic function]),复合起来,则称为逻辑回归函数。
- 逻辑函数是 S 形函数,会将所有实数映射到 ( 0 , 1 ) (0, 1) (0,1) 范围。
- [sigmoid 函数](如下图)是逻辑函数的特殊情况,其公式为 g ( z ) = 1 1 + e − z g\left( z \right)=\frac{1}{1+{{e}^{-z}}} g(z)=1+e−z1。

- 应用 sigmoid 函数,则逻辑回归模型: h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x h_{\theta}(x)=g(\theta^Tx) =\frac{1}{1+e^{-\theta^Tx}} hθ(x)=g(θTx)=1+e−θTx1
逻辑回归模型中, h θ ( x ) h_\theta \left( x \right) hθ(x) 的作用是,根据输入 x x x 以及参数 θ \theta θ,计算得出”输出 y = 1 y=1 y=1“的可能性(estimated probability),概率学中表示为:
- h θ ( x ) = P ( y = 1 ∣ x ; θ ) = 1 − P ( y = 0 ∣ x ; θ ) h_{\theta}(x) = P(y=1|x;{\theta}) = 1 - P(y=0|x;{\theta}) hθ(x)=P(y=1∣x;θ)=1−P(y=0∣x;θ)
- P ( y = 0 ∣ x ; θ ) + P ( y = 1 ∣ x ; θ ) = 1 P(y = 0|x;\theta) + P(y = 1 | x ; \theta) = 1 P(y=0∣x;θ)+P(y=1∣x;θ)=1
3.1.2 决策边界(Decision Boundary)
决策边界的概念,可帮助我们更好地理解逻辑回归模型的拟合原理。
在逻辑回归中,有假设函数 h θ ( x ) = g ( z ) = g ( θ T x ) h_\theta \left( x \right)=g(z)=g\left(\theta^{T}x \right) hθ(x)=g(z)=g(θTx)。
为了得出分类的结果,这里和前面一样,规定以 0.5 0.5 0.5 为阈值:
- h θ ( x ) ≥ 0.5 → y = 1 h_\theta(x) \geq 0.5 \rightarrow y = 1 \newline hθ(x)≥0.5→y=1
- h θ ( x ) < 0.5 → y = 0 h_\theta(x) < 0.5 \rightarrow y = 0 \newline hθ(x)<0.5→y=0
观察上图的sigmoid 函数的图像:
可得当 g ( z ) ≥ 0.5 g(z) \geq 0.5 g(z)≥0.5 时,有 z ≥ 0 z \geq 0 z≥0,即 θ T x ≥ 0 \theta^Tx \geq 0 θTx≥0。
同线性回归模型的不同点在于:
- z → + ∞ , e − ∞ → 0 ⇒ g ( z ) = 1 z \to +\infty, e^{-\infty} \to 0 \Rightarrow g(z)=1 z→+∞,e−∞→0⇒g(z)=1
- z → − ∞ , e ∞ → ∞ ⇒ g ( z ) = 0 z \to -\infty, e^{\infty}\to \infty \Rightarrow g(z)=0 z→−∞,e∞→∞⇒g(z)=0
直观一点来个例子, h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 ) {h_\theta}\left( x \right)=g\left( {\theta_0}+{\theta_1}{x_1}+{\theta_{2}}{x_{2}}\right) hθ(x)=g(θ0+θ1x1+θ2x2) 是下图模型的假设函数:

根据上面的讨论,要进行分类,那么只要 θ 0 + θ 1 x 1 + θ 2 x 2 ≥ 0 {\theta_0}+{\theta_1}{x_1}+{\theta_{2}}{x_{2}}\geq0 θ0+θ1x1+θ2x2≥0 时,就预测 y = 1 y = 1 y=1,即预测为正向类。
如果取 θ = [ − 3 1 1 ] \theta = \begin{bmatrix} -3\\1\\1\end{bmatrix} θ=⎣⎡−311⎦⎤,则有 z = − 3 + x 1 + x 2 z = -3+{x_1}+{x_2} z=−3+x1+x2,当 z ≥ 0 z \geq 0 z≥0 即 x 1 + x 2 ≥ 3 {x_1}+{x_2} \geq 3 x1+x2≥3 时,易绘制图中的品红色直线即决策边界,为正向类(以红叉标注的数据)给出 y = 1 y=1 y=1 的分类预测结果。
简单来说,决策边界就是分类的分界线,分类现在实际就由 z z z (中的 θ \theta θ)决定啦。
3.1.3 代价函数(Cost Function)
那我们怎么知道决策边界是啥样? θ \theta θ 多少时能很好的拟合数据?当然,见招拆招,总要来个 J ( θ ) J(\theta) J(θ)。
如果直接套用线性回归的代价函数: J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( {\theta} \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( h_{\theta} \left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
其中 h θ ( x ) = g ( θ T x ) h_\theta(x) = g\left(\theta^{T}x \right) hθ(x)=g(θTx),可绘制关于 J ( θ ) J(\theta) J(θ) 的图像,如下图
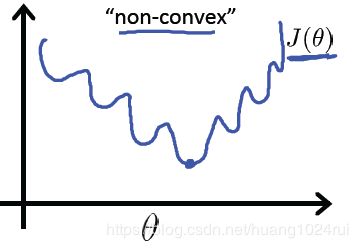
回忆线性回归中的平方损失函数,其是一个二次凸函数(碗状),二次凸函数的重要性质是只有一个局部最小点即全局最小点。上图中有许多局部最小点,这样将使得梯度下降算法无法确定收敛点是全局最优。

如果此处的损失函数也是一个凸函数,是否也有同样的性质,根据优化理论的性质,这类讨论凸函数最优值的问题,被称为凸优化问题(Convex optimization)。
当然,损失函数不止平方损失函数一种。
对于逻辑回归,更换平方损失函数为 对 数 损 失 函 数 \color{red}对数损失函数 对数损失函数,可由统计学中的最大似然估计方法推出代价函数 J ( θ ) J(\theta) J(θ):
J ( θ ) = 1 m ∑ i = 1 m cost ( h θ ( x ( i ) ) , y ( i ) ) J(\theta)=\frac{1}{m} \sum_{i=1}^{m} \operatorname{cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right) J(θ)=m1∑i=1mcost(hθ(x(i)),y(i))
- cost ( h θ ( x ) , y ) = − log ( h θ ( x ) ) \operatorname{cost}\left(h_{\theta}(x), y\right)=-\log \left(h_{\theta}(x)\right) \quad cost(hθ(x),y)=−log(hθ(x)) if y = 1 \mathrm{y}=1 y=1
- cost ( h θ ( x ) , y ) = − log ( 1 − h θ ( x ) ) \operatorname{cost}\left(h_{\theta}(x), y\right)=-\log \left(1-h_{\theta}(x)\right) cost(hθ(x),y)=−log(1−hθ(x)) if y = 0 \mathrm{y}=0 y=0
则有关于 J ( θ ) J(\theta) J(θ) 的图像如下:
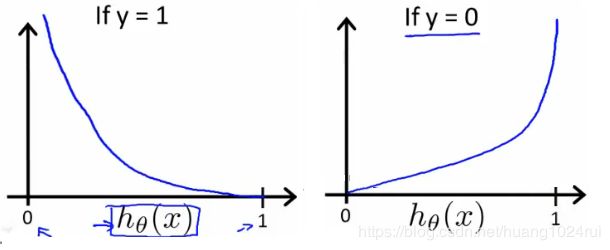
如左图,当训练集的结果为 y = 1 y=1 y=1(正样本)时,随着假设函数趋向于 1 1 1,代价函数的值会趋于 0 0 0,即意味着拟合程度很好。如果假设函数此时趋于 0 0 0,则会给出一个很高的代价,拟合程度差,算法会根据其迅速纠正 θ \theta θ 值,右图 y = 0 y=0 y=0 同理。
区别于平方损失函数,对数损失函数也是一个凸函数,但没有局部最优值。
3.1.4 简化的成本函数和梯度下降(Simplified Cost Function and Gradient Descent)
-
代价函数
为了便于计算,对于二元分类问题,我们可把代价函数简化为一个函数:
C o s t ( h θ ( x ) , y ) = − y × l o g ( h θ ( x ) ) − ( 1 − y ) × l o g ( 1 − h θ ( x ) ) Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right) Cost(hθ(x),y)=−y×log(hθ(x))−(1−y)×log(1−hθ(x))当 y = 0 y = 0 y=0,左边式子整体为 0 0 0,当 y = 1 y = 1 y=1,则 1 − y = 0 1-y=0 1−y=0,右边式子整体为0,也就和上面的分段函数一样了,而一个式子计算起来更方便。
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(\theta) = - \frac{1}{m} \displaystyle \sum_{i=1}^m [y^{(i)}\log (h_\theta (x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)}))] J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]向量化实现:
h = g ( X θ ) h = g(X\theta) h=g(Xθ), J ( θ ) = 1 m ⋅ ( − y T log ( h ) − ( 1 − y ) T log ( 1 − h ) ) J(\theta) = \frac{1}{m} \cdot \left(-y^{T}\log(h)-(1-y)^{T}\log(1-h)\right) J(θ)=m1⋅(−yTlog(h)−(1−y)Tlog(1−h))
为了最优化 θ \theta θ,仍使用梯度下降法,算法同线性回归中一致:
repeat until convergence:{
θ j : = θ j − α ∂ ∂ θ j J ( θ ) \theta_{j}:={{\theta }_{j}}-\alpha \frac{\partial }{\partial {{\theta }_{j}}}J\left( {\theta} \right) θj:=θj−α∂θj∂J(θ)
}解出偏导得:
repeat until convergence:{
θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) for j := 0,1...n \theta_j := \theta_j - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \; \;\; \text{for j := 0,1...n} θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))⋅xj(i)for j := 0,1...n
}
注意,虽然形式上梯度下降算法同线性回归一样,但其中的假设函不同,即 h θ ( x ) = g ( θ T x ) h_\theta(x) = g\left(\theta^{T}x \right) hθ(x)=g(θTx),不过求导后的结果也相同。
向量化实现: θ : = θ − α m X T ( g ( X θ ) − y ) \theta := \theta - \frac{\alpha}{m} X^{T} (g(X \theta ) - y) θ:=θ−mαXT(g(Xθ)−y)
-
逻辑回归中代价函数求导的推导过程:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(\theta) = - \frac{1}{m} \displaystyle \sum_{i=1}^m [y^{(i)}\log (h_\theta (x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)}))] J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
令 f ( θ ) = y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) f(\theta) = {{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right) f(θ)=y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))
忆及 h θ ( x ) = g ( z ) h_\theta(x) = g(z) hθ(x)=g(z), g ( z ) = 1 1 + e ( − z ) g(z) = \frac{1}{1+e^{(-z)}} g(z)=1+e(−z)1,则
f ( θ ) = y ( i ) log ( 1 1 + e − z ) + ( 1 − y ( i ) ) log ( 1 − 1 1 + e − z ) f(\theta)={{y}^{(i)}}\log \left( \frac{1}{1+{{e}^{-z}}} \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-\frac{1}{1+{{e}^{-z}}} \right) f(θ)=y(i)log(1+e−z1)+(1−y(i))log(1−1+e−z1)
= − y ( i ) log ( 1 + e − z ) − ( 1 − y ( i ) ) log ( 1 + e z ) =-{{y}^{(i)}}\log \left( 1+{{e}^{-z}} \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1+{{e}^{z}} \right) =−y(i)log(1+e−z)−(1−y(i))log(1+ez)忆及 z = θ T x ( i ) z=\theta^Tx^{(i)} z=θTx(i),对 θ j \theta_j θj 求偏导则没有 θ j \theta_j θj 的项求偏导即为 0 0 0,都消去,则得:
∂ z ∂ θ j = ∂ ∂ θ j ( θ T x ( i ) ) = x j ( i ) \frac{\partial z}{\partial {\theta_{j}}}=\frac{\partial }{\partial {\theta_{j}}}\left( \theta^Tx^{(i)} \right)=x^{(i)}_j ∂θj∂z=∂θj∂(θTx(i))=xj(i)
所以有:
∂ ∂ θ j f ( θ ) = ∂ ∂ θ j [ − y ( i ) log ( 1 + e − z ) − ( 1 − y ( i ) ) log ( 1 + e z ) ] \frac{\partial }{\partial {\theta_{j}}}f\left( \theta \right)=\frac{\partial }{\partial {\theta_{j}}}[-{{y}^{(i)}}\log \left( 1+{{e}^{-z}} \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1+{{e}^{z}} \right)] ∂θj∂f(θ)=∂θj∂[−y(i)log(1+e−z)−(1−y(i))log(1+ez)]
= − y ( i ) ∂ ∂ θ j ( − z ) e − z 1 + e − z − ( 1 − y ( i ) ) ∂ ∂ θ j ( z ) e z 1 + e z =-{{y}^{(i)}}\frac{\frac{\partial }{\partial {\theta_{j}}}\left(-z \right) e^{-z}}{1+e^{-z}}-\left( 1-{{y}^{(i)}} \right)\frac{\frac{\partial }{\partial {\theta_{j}}}\left(z \right){e^{z}}}{1+e^{z}} =−y(i)1+e−z∂θj∂(−z)e−z−(1−y(i))1+ez∂θj∂(z)ez
= − y ( i ) − x j ( i ) e − z 1 + e − z − ( 1 − y ( i ) ) x j ( i ) 1 + e − z =-{{y}^{(i)}}\frac{-x^{(i)}_je^{-z}}{1+e^{-z}}-\left( 1-{{y}^{(i)}} \right)\frac{x^{(i)}_j}{1+e^{-z}} =−y(i)1+e−z−xj(i)e−z−(1−y(i))1+e−zxj(i)
= ( y ( i ) e − z 1 + e − z − ( 1 − y ( i ) ) 1 1 + e − z ) x j ( i ) =\left({{y}^{(i)}}\frac{e^{-z}}{1+e^{-z}}-\left( 1-{{y}^{(i)}} \right)\frac{1}{1+e^{-z}}\right)x^{(i)}_j =(y(i)1+e−ze−z−(1−y(i))1+e−z1)xj(i)
= ( y ( i ) e − z 1 + e − z − ( 1 − y ( i ) ) 1 1 + e − z ) x j ( i ) =\left({{y}^{(i)}}\frac{e^{-z}}{1+e^{-z}}-\left( 1-{{y}^{(i)}} \right)\frac{1}{1+e^{-z}}\right)x^{(i)}_j =(y(i)1+e−ze−z−(1−y(i))1+e−z1)xj(i)
= ( y ( i ) ( e − z + 1 ) − 1 1 + e − z ) x j ( i ) =\left(\frac{{{y}^{(i)}}(e^{-z}+1)-1}{1+e^{-z}}\right)x^{(i)}_j =(1+e−zy(i)(e−z+1)−1)xj(i)
= ( y ( i ) − 1 1 + e − z ) x j ( i ) ={({{y}^{(i)}}-\frac{1}{1+{{e}^{-z}}})x_j^{(i)}} =(y(i)−1+e−z1)xj(i) = ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) ={\left({{y}^{(i)}}-{h_\theta}\left( {{x}^{(i)}} \right)\right)x_j^{(i)}} =(y(i)−hθ(x(i)))xj(i) = − ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) =-{\left({h_\theta}\left( {{x}^{(i)}} \right)-{{y}^{(i)}}\right)x_j^{(i)}} =−(hθ(x(i))−y(i))xj(i)则可得代价函数的导数:
∂ ∂ θ j J ( θ ) = − 1 m ∑ i = 1 m ∂ ∂ θ j f ( θ ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) \frac{\partial}{\partial \theta_{j}} J(\theta)=-\frac{1}{m} \sum_{i=1}^{m} \frac{\partial}{\partial \theta_{j}} f(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{j}^{(i)} ∂θj∂J(θ)=−m1i=1∑m∂θj∂f(θ)=m1i=1∑m(hθ(x(i))−y(i))⋅xj(i)
3.1.5 进阶优化(Advanced Optimization)
运行梯度下降算法,其能最小化代价函数 J ( θ ) J(\theta) J(θ) 并得出 θ \theta θ 的最优值,在使用梯度下降算法时,如果不需要观察代价函数的收敛情况,则直接计算 J ( θ ) J(\theta) J(θ) 的导数项即可,而不需要计算 J ( θ ) J(\theta) J(θ) 值。
我们编写代码给出代价函数及其偏导数然后传入梯度下降算法中,接下来算法则会为我们最小化代价函数给出参数的最优解。这类算法被称为最优化算法(Optimization Algorithms),梯度下降算法不是唯一的最小化算法[^1]。
一些最优化算法:
- 梯度下降法(Gradient Descent)
- 共轭梯度算法(Conjugate gradient)
- 牛顿法和拟牛顿法(Newton’s method & Quasi-Newton Methods)
- DFP算法
- 局部优化法(BFGS)
- 有限内存局部优化法(L-BFGS)
- 拉格朗日乘数法(Lagrange multiplier)
比较梯度下降算法:一些最优化算法虽然会更为复杂,难以调试,自行实现又困难重重,开源库又效率也不一,哎,做个调包侠还得碰运气。不过这些算法通常效率更高,并无需选择学习速率 α \alpha α(少一个参数少一份痛苦啊!)。
Octave/Matlab 中对这类高级算法做了封装,易于调用。
假设有 J ( θ ) = ( θ 1 − 5 ) 2 + ( θ 2 − 5 ) 2 J(\theta) = (\theta_1-5)^2 + (\theta_2-5)^2 J(θ)=(θ1−5)2+(θ2−5)2,要求参数 θ = [ θ 1 θ 2 ] \theta=\begin{bmatrix} \theta_1\\\theta_2\end{bmatrix} θ=[θ1θ2]的最优值。
下面为 Octave/Matlab 求解最优化问题的代码实例:
- 创建一个函数以返回代价函数及其偏导数:
function [jVal, gradient] = costFunction(theta)
% code to compute J(theta)
jVal=(theta(1)-5)^2+(theta(2)-5)^2;
% code to compute derivative of J(theta)
gradient=zeros(2,1);
gradient(1)=2*(theta(1)-5);
gradient(2)=2*(theta(2)-5);
end
- 将
costFunction函数及所需参数传入最优化函数fminunc,以求解最优化问题:
options = optimset('GradObj', 'on', 'MaxIter', 100);
initialTheta = zeros(2,1);
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);
'GradObj', 'on': 启用梯度目标参数(则需要将梯度传入算法)
'MaxIter', 100: 最大迭代次数为 100 次
@xxx: Octave/Matlab 中的函数指针
optTheta: 最优化得到的参数向量
functionVal: 引用函数最后一次的返回值
exitFlag: 标记代价函数是否收敛
注:Octave/Matlab 中可以使用 help fminunc 命令随时查看函数的帮助文档。
- 返回结果
optTheta =
5
5
functionVal = 0
exitFlag = 1
3.1.6 多类别分类: 一对多(Multiclass Classification: One-vs-all)
原理是,转化多类别分类问题为多个二元分类问题,这种方法被称为 One-vs-all。
正式定义: h θ ( i ) ( x ) = p ( y = i ∣ x ; θ ) , i = ( 1 , 2 , 3.... k ) h_\theta^{\left( i \right)}\left( x \right)=p\left( y=i|x;\theta \right), i=\left( 1,2,3....k \right) hθ(i)(x)=p(y=i∣x;θ),i=(1,2,3....k)
h θ ( i ) ( x ) h_\theta^{\left( i \right)}\left( x \right) hθ(i)(x): 输出 y = i y=i y=i(属于第 i i i 个分类)的可能性
k k k: 类别总数,如 k = 3 k=3 k=3。
注意多类别分类问题中 h θ ( x ) h_\theta(x) hθ(x) 的结果不再只是一个实数而是一个向量,如果类别总数为 k k k,现在 h θ ( x ) h_\theta(x) hθ(x) 就是一个 k k k 维向量。
对于某个样本实例,需计算所有的 k k k 种分类情况得到 h θ ( x ) h_\theta(x) hθ(x),然后看分为哪个类别时预测输出的值最大,就说它输出属于哪个类别,即 y = max i h θ ( i ) ( x ) y = \mathop{\max}\limits_i\,h_\theta^{\left( i \right)}\left( x \right) y=imaxhθ(i)(x)。
3.2 正则化(Regularization)
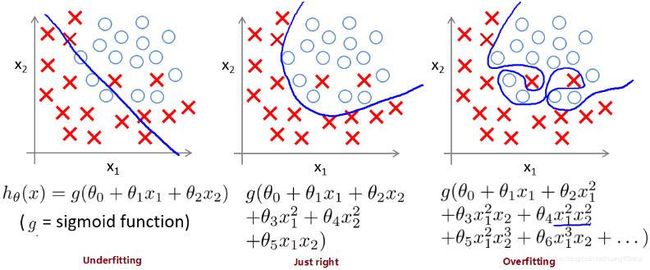
3.2.1 过拟合问题(The Problem of Overfitting)
对于拟合的表现,可以分为三类情况:
-
欠拟合(Underfitting)
无法很好的拟合训练集中的数据,预测值和实际值的误差很大,这类情况被称为欠拟合。拟合模型比较简单(特征选少了)时易出现这类情况。类似于,你上课不好好听,啥都不会,下课也差不多啥都不会。
-
优良的拟合(Just right)
不论是训练集数据还是不在训练集中的预测数据,都能给出较为正确的结果。类似于,学霸学神!
-
过拟合(Overfitting)
能很好甚至完美拟合训练集中的数据,即 J ( θ ) → 0 J(\theta) \to 0 J(θ)→0,但是对于不在训练集中的新数据,预测值和实际值的误差会很大,泛化能力弱,这类情况被称为过拟合。拟合模型过于复杂(特征选多了)时易出现这类情况。类似于,你上课跟着老师做题都会都听懂了,下课遇到新题就懵了不会拓展。
为了度量拟合表现,引入:
-
偏差(bias)
指模型的预测值与真实值的偏离程度。偏差越大,预测值偏离真实值越厉害。偏差低意味着能较好地反应训练集中的数据情况。
-
方差(Variance)
指模型预测值的离散程度或者变化范围。方差越大,数据的分布越分散,函数波动越大,泛化能力越差。方差低意味着拟合曲线的稳定性高,波动小。

据上图,高偏差意味着欠拟合,高方差意味着过拟合。
我们应尽量使得拟合模型处于低方差(较好地拟合数据)状态且同时处于低偏差(较好地预测新值)的状态。
避免过拟合的方法有:
- 减少特征的数量
- 手动选取需保留的特征
- 使用模型选择算法来选取合适的特征(如 PCA 算法)
- 减少特征的方式易丢失有用的特征信息
- 正则化(Regularization)
- 可保留所有参数(许多有用的特征都能轻微影响结果)
- 减少/惩罚各参数大小(magnitude),以减轻各参数对模型的影响程度
- 当有很多参数对于模型只有轻微影响时,正则化方法的表现很好
3.2.2 代价函数(Cost Function)
很多时候由于特征数量过多,过拟合时我们很难选出要保留的特征,这时候应用正则化方法则是很好的选择。
上文中, θ 0 + θ 1 x + θ 2 x 2 + θ 3 x 3 + θ 4 x 4 \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + \theta_4x^4 θ0+θ1x+θ2x2+θ3x3+θ4x4 这样一个复杂的多项式较易过拟合,在不减少特征的情况下,如果能消除类似于 θ 3 x 3 \theta_3x^3 θ3x3、 θ 4 x 4 \theta_4x^4 θ4x4 等复杂部分,那复杂函数就变得简单了。
为了保留各个参数的信息,不修改假设函数,改而修改代价函数:
m i n θ 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + 1000 ⋅ θ 3 2 + 1000 ⋅ θ 4 2 min_\theta\ \dfrac{1}{2m}\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + 1000\cdot\theta_3^2 + 1000\cdot\theta_4^2 minθ 2m1∑i=1m(hθ(x(i))−y(i))2+1000⋅θ32+1000⋅θ42
上式中,我们在代价函数中增加了 θ 3 \theta_3 θ3、 θ 4 \theta_4 θ4 的惩罚项(penalty term) 1000 ⋅ θ 3 2 + 1000 ⋅ θ 4 2 1000\cdot\theta_3^2 + 1000\cdot\theta_4^2 1000⋅θ32+1000⋅θ42,如果要最小化代价函数,那么势必需要极大地减小 θ 3 \theta_3 θ3、 θ 4 \theta_4 θ4,从而使得假设函数中的 θ 3 x 3 \theta_3x^3 θ3x3、 θ 4 x 4 \theta_4x^4 θ4x4 这两项的参数非常小,就相当于没有了,假设函数也就**“变得”简单**了,从而在保留各参数的情况下避免了过拟合问题。

根据上面的讨论,有时也无法决定要减少哪个参数,故统一惩罚除了 θ 0 \theta_0 θ0 外的所有参数。
代价函数:
J ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ] J\left( \theta \right)=\frac{1}{2m}[\sum\limits_{i=1}^{m}{{{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}+\lambda \sum\limits_{j=1}^{n}{\theta_{j}^{2}}]} J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2]
λ \lambda λ: 正则化参数(Regularization Parameter), λ > 0 \lambda > 0 λ>0
∑ j = 1 n \sum\limits_{j=1}^{n} j=1∑n: 不惩罚基础参数 θ 0 \theta_0 θ0
λ ∑ j = 1 n θ j 2 \lambda \sum\limits_{j=1}^{n}{\theta_{j}^{2}} λj=1∑nθj2: 正则化项
λ \lambda λ 正则化参数类似于学习速率,也需要我们自行对其选择一个合适的值。
- 过大
- 导致模型欠拟合(假设可能会变成近乎 x = θ 0 x = \theta_0 x=θ0 的直线 )
- 无法正常去过拟问题
- 梯度下降可能无法收敛
- 过小
- 无法避免过拟合(等于没有)
正则化符合奥卡姆剃刀(Occam’s razor)原理。在所有可能选择的模型中,能够很好地解释已知数据并且十分简单才是最好的模型,也就是应该选择的模型。从贝叶斯估计的角度来看,正则化项对应于模型的先验概率。可以假设复杂的模型有较大的先验概率,简单的模型有较小的先验概率。
正则化是结构风险最小化策略的实现,是去过拟合问题的典型方法,虽然看起来多了个一参数多了一重麻烦,后文会介绍自动选取正则化参数的方法。模型越复杂,正则化参数值就越大。比如,正则化项可以是模型参数向量的范数。
3.2.3 线性回归正则化(Regularized Linear Regression)
应用正则化的线性回归梯度下降算法:
Repeat { θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) θ j : = θ j − α [ ( 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ) + λ m θ j ] , j ∈ { 1 , 2 … n } \begin{array}{l} \theta_{0}:=\theta_{0}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{0}^{(i)} \\ \theta_{j}:=\theta_{j}-\alpha\left[\left(\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}\right)+\frac{\lambda}{m} \theta_{j}\right], \quad j \in\{1,2 \ldots n\} \end{array} θ0:=θ0−αm1∑i=1m(hθ(x(i))−y(i))x0(i)θj:=θj−α[(m1∑i=1m(hθ(x(i))−y(i))xj(i))+mλθj],j∈{1,2…n}}
也可以移项得到更新表达式的另一种表示形式
θ j : = θ j ( 1 − α λ m ) − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j := \theta_j(1 - \alpha\frac{\lambda}{m}) - \alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} θj:=θj(1−αmλ)−αm1∑i=1m(hθ(x(i))−y(i))xj(i)
1. λ m θ j \frac{\lambda}{m}\theta_j mλθj: 正则化项
2.也可以形象化的看出,正则化 θ j \theta_j θj可以看成对 θ j \theta_j θj的惩罚。
应用正则化的正规方程法:
θ = ( X T X + λ ⋅ L ) − 1 X T y \theta=\left(X^{T} X+\lambda \cdot L\right)^{-1} X^{T} y θ=(XTX+λ⋅L)−1XTy
where L = [ 0 1 1 ⋱ 1 ] L=\left[\begin{array}{ccccc}0 \\ & 1 \\ & & 1 \\ & & & \ddots \\ & & & & 1\end{array}\right] L=⎣⎢⎢⎢⎢⎡011⋱1⎦⎥⎥⎥⎥⎤
λ ⋅ L \lambda\cdot L λ⋅L: 正则化项
L L L: 第一行第一列为 0 0 0 的 n + 1 n+1 n+1 维单位矩阵
matlab中用:pinv求伪逆
Matlab/Octave 代码:
>> L = eye(5)
>> L(1,1) = 0
L =
0 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
前文提到正则化可以解决正规方程法中不可逆的问题,即增加了 λ ⋅ L \lambda \cdot L λ⋅L 正则化项后,可以保证 X T X + λ ⋅ L X^TX + \lambda \cdot L XTX+λ⋅L 可逆(invertible),即便 X T X X^TX XTX 不可逆(non-invertible)。
3.2.4 逻辑回归正则化(Regularized Logistic Regression)
为逻辑回归的代价函数添加正则化项:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta) = - \frac{1}{m} \sum_{i=1}^m \large[ y^{(i)}\ \log (h_\theta (x^{(i)})) + (1 - y^{(i)})\ \log (1 - h_\theta(x^{(i)}))\large] + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2 J(θ)=−m1∑i=1m[y(i) log(hθ(x(i)))+(1−y(i)) log(1−hθ(x(i)))]+2mλ∑j=1nθj2
前文已经证明过逻辑回归和线性回归的代价函数的求导结果是一样的,此处通过给正则化项添加常数 1 2 \frac{1}{2} 21,则其求导结果也就一样了。
从而有应用正则化的逻辑回归梯度下降算法:
Repeat { θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) θ j : = θ j − α [ ( 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ) + λ m θ j ] , j ∈ { 1 , 2 … n } \begin{array}{l} \theta_{0}:=\theta_{0}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{0}^{(i)} \\ \theta_{j}:=\theta_{j}-\alpha\left[\left(\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}\right)+\frac{\lambda}{m} \theta_{j}\right], \quad j \in\{1,2 \ldots n\} \end{array} θ0:=θ0−αm1∑i=1m(hθ(x(i))−y(i))x0(i)θj:=θj−α[(m1∑i=1m(hθ(x(i))−y(i))xj(i))+mλθj],j∈{1,2…n}}
4. Week 4(神经网络:表达(Neural Networks: Representation))
4.1 非线性假设(Non-linear Hypotheses)
理论上我们可以用多项式函数去近似任意函数(泰勒极数(Taylor series)),从而可得到任意问题的拟合曲线。
在实际处理时,特征量通常会很多,如果再构造高阶多项式等,特征数量将会急剧增加,这使得回归模型的复杂度太高,可见并不合适。神经网络无需构造高阶多项式,在特征量很大时也可以处理的很好。
那特征能有多大呢?下面是一个计算机视觉中的例子:

如上图,如果选取一小块 50 ∗ 50 50 * 50 50∗50 像素的灰度图片(一个像素只有亮度一个值),选择每个像素点作为特征,则特征总量 n = 2500 n=2500 n=2500(换成 RGB(一个像素有三个值),则 n = 7500 n = 7500 n=7500),如果将其两两组合作为新特征,则特征数量将为 C 2500 2 ≈ 3 m i l l i o n C_{2500}^{2} \approx 3\ million C25002≈3 million。普通的逻辑回归模型,不能有效地处理这么多的特征,这时候我们需要神经网络。
4.2 神经网络和大脑(Neurons and the Brain)
脑科学家通过对动物实验,发现大脑中专用于处理听觉信号的脑皮层也能处理其他诸如视觉等信号,即如果切断其与耳朵的联系,将其与眼睛相连,则这块负责听觉的脑皮层区域也能接受并处理视觉信号,从而学会“看”。脑科学家通过这类换源实验,就推论假设大脑的学习算法只有一种(“one learning algorithm” hypothesis)。那么如果能找出这种学习算法并应用于计算机中,那梦想中和人一样的人工智能就成真了。
神经网络就源于模拟人类大脑,但其需要的计算量很大。随着计算机硬件性能的提高,神经网络逐渐从衰落变为流行,如今已广泛地被应用在各行各业中。
下图是根据研究做的一些应用(有兴趣可回顾视频):

BrainPort 系统:帮助失明人士通过摄像头以及舌尖感官“看”东西

触觉皮带:在朝北时蜂鸣器会发出声响,可使人拥有方向感(声音信号转换为方向信号)。
从某种意义上来说,如果我们能找出大脑的学习算法,然后在计算机上执行大脑学习算法或与之相似的算法,也许这将是我们向人工智能迈进做出的最好的尝试。
人工智能的梦想就是:有一天能制造出真正的智能机器。
4.3 模型表示1(Model Representation I)
既然神经网络模仿的是大脑神经元,那就先看一下大脑的神经元长什么样吧:
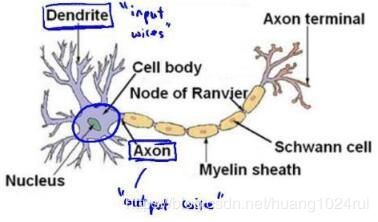
想象一下印刷厂中流水线的工人,每个工人都有特定的任务,比如装订,塑封,贴防伪标识等等,工人们看到书本并处理完自己的任务后,就回放回传送带,紧接着传送带就传给下一个环节的工人,如此不断重复从而完成一个又一个环节,直到一本书印制完成。
那么类比一下,把上图中的细胞核(nucleus) 类比成工人,轴突(axon) 类比传送带,树突(dendrite) 则比类比成工人的双眼。一个又一个细胞体,从树突接收需要处理的信息,对其进行处理后,再经由轴突通过电信号把处理完的信息传递出去,直到理解信息的内容。当然啦,我们大脑的实际上还要更为复杂,而且一个人的神经元数目就比地球上所有流水线的工人之和还要多呢~
人工神经网络中,树突对应输入(input),细胞核对应激活单元(activation unit),轴突对应输出(output)。
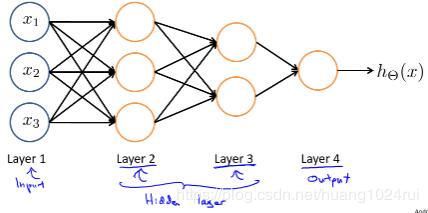
我们一般把神经网络划分为三部分(注意,不是只有三层!),即输入层(input layer),隐藏层(hidden layer)和输出层(output layer)。
图中的一个圈表示神经网络中的一个激活单元,输入层对应输入单元,隐藏层对应中间单元,输出层则对应输出单元。中间激活单元应用激活函数(activation_function)处理数据。
下面列出一些已有概念在神经网络中的别称:
- x 0 x_0 x0: 偏置单元(bias unit), x 0 x_0 x0=1
- Θ \Theta Θ: 权重(weight),即参数。
- 激活函数: g g g,即逻辑函数等。
- 输入层: 对应于训练集中的特征 x x x。
- 输出层: 对应于训练集中的结果 y y y。
- a i ( j ) a^{(j)}_i ai(j): 第 j j j 层的第 i i i 个激活单元。
- Θ ( j ) \Theta^{(j)} Θ(j): 从第 j j j 层映射到第 j + 1 j+1 j+1 层时的权重矩阵。
- Θ v , u ( j ) \Theta^{(j)}_{v,u} Θv,u(j): 从第 j j j 层的第 u u u 个单元映射到第 j + 1 j+1 j+1 层的第 v v v 个单元的权重。
- s j s_j sj: 第 j j j 层的激活单元数目(不包含偏置单元)。
注意:
- 每个单元会作用于下一层的所有单元(矩阵乘法运算)。
- 如果第 j j j 层有 s j s_j sj 个单元,第 j + 1 j+1 j+1 层有 s j + 1 s_{j+1} sj+1 个单元, Θ ( j ) \Theta^{(j)} Θ(j) 是一个 s j + 1 × ( s j + 1 ) s_{j+1} \times (s_j+1) sj+1×(sj+1) 维的权重矩阵。即每一层的权重矩阵大小都是非固定的。
- 其中, + 1 ( x 0 , a 0 ( 2 ) ) +1(x_0,a^{(2)}_0) +1(x0,a0(2)) 来自于偏置单元,这样意味着输出层不包含偏置单元,输入层和隐藏层需要增加偏置单元。
依据本节所给模型,有:
- s i z e o f ( Θ ( 1 ) ) = s j + 1 × ( s j + 1 ) = s 2 × ( s 1 + 1 ) = 3 × 4 sizeof (\Theta^{(1)})=s_{j+1} \times (s_j + 1) =s_2 \times (s_1 + 1) = 3 \times 4 sizeof(Θ(1))=sj+1×(sj+1)=s2×(s1+1)=3×4
- s i z e o f ( Θ ( 2 ) ) = s 3 × ( s 2 + 1 ) = 1 × 4 sizeof (\Theta^{(2)})=s_3 \times (s_2 + 1) = 1 \times 4 sizeof(Θ(2))=s3×(s2+1)=1×4
4.4 模型表示2(Model Representation II)
对**输入层(Layer 1)**的所有激活单元应用激活函数,从而得到隐藏层(Layer 2)中激活单元的值:
a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3) a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3) a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)
a 3 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) a_3^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3) a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)
对 Layer 2 中的所有激活单元应用激活函数,从而得到输出:
h Θ ( x ) = a 1 ( 3 ) = g ( Θ 10 ( 2 ) a 0 ( 2 ) + Θ 11 ( 2 ) a 1 ( 2 ) + Θ 12 ( 2 ) a 2 ( 2 ) + Θ 13 ( 2 ) a 3 ( 2 ) ) h_\Theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)}) hΘ(x)=a1(3)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
上面的计算过程被称为 前向传播(Forward propagation),即从输入层开始,一层一层地向下计算并传递结果。
再回顾一下逻辑回归:
h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 ) {h_\theta}\left( x \right)=g\left( {\theta_0}+{\theta_1}{x_1}+{\theta_{2}}{x_{2}}+{\theta_{3}}x_3 \right) hθ(x)=g(θ0+θ1x1+θ2x2+θ3x3)
是不是除了符号表示,其他都完全一样?其实神经网络就好似回归模型,只不过输入变成了中间单元 a 1 ( j ) , a 2 ( j ) , … , a n ( j ) a_1^{(j)}, a_2^{(j)}, \dots, a_n^{(j)} a1(j),a2(j),…,an(j)。从输入 x x x 开始,下一层的每个激活单元都包含了上一层的所有信息(单元值),通过最优化算法不断迭代计算,激活单元能得出关于输入 x x x 的更多信息,这就好像是在给假设函数加多项式。隐藏层的这些单元好似升级版的初始特征,从而能给出更好的预测。
向量化实现
定义 a ( 1 ) = x = [ x 0 x 1 x 2 x 3 ] a^{(1)}=x=\left[ \begin{matrix}x_0\\ x_1 \\ x_2 \\ x_3 \end{matrix} \right] a(1)=x=⎣⎢⎢⎡x0x1x2x3⎦⎥⎥⎤, Θ ( 1 ) = [ Θ 10 ( 1 ) Θ 11 ( 1 ) Θ 12 ( 1 ) Θ 13 ( 1 ) Θ 20 ( 1 ) Θ 21 ( 1 ) Θ 22 ( 1 ) Θ 23 ( 1 ) Θ 30 ( 1 ) Θ 31 ( 1 ) Θ 32 ( 1 ) Θ 33 ( 1 ) ] \Theta^{(1)}=\left[\begin{matrix}\Theta^{(1)}_{10}& \Theta^{(1)}_{11}& \Theta^{(1)}_{12}& \Theta^{(1)}_{13}\\ \Theta^{(1)}_{20}& \Theta^{(1)}_{21}& \Theta^{(1)}_{22}& \Theta^{(1)}_{23}\\ \Theta^{(1)}_{30}& \Theta^{(1)}_{31}& \Theta^{(1)}_{32} & \Theta^{(1)}_{33}\end{matrix}\right] Θ(1)=⎣⎢⎡Θ10(1)Θ20(1)Θ30(1)Θ11(1)Θ21(1)Θ31(1)Θ12(1)Θ22(1)Θ32(1)Θ13(1)Θ23(1)Θ33(1)⎦⎥⎤,
a 1 ( 2 ) = g ( z 1 ( 2 ) ) a_1^{(2)} = g(z_1^{(2)}) a1(2)=g(z1(2)) , a 2 ( 2 ) = g ( z 2 ( 2 ) ) a_2^{(2)} = g(z_2^{(2)}) a2(2)=g(z2(2)), a 3 ( 2 ) = g ( z 3 ( 2 ) ) a_3^{(2)} = g(z_3^{(2)}) a3(2)=g(z3(2)),
z ( 2 ) = [ z 1 ( 2 ) z 2 ( 2 ) z 3 ( 2 ) ] z^{(2)}=\left[ \begin{matrix}z_1^{(2)}\\ z_2^{(2)} \\ z_3^{(2)}\end{matrix} \right] z(2)=⎣⎢⎡z1(2)z2(2)z3(2)⎦⎥⎤
则有 a ( 2 ) = g ( Θ ( 1 ) a ( 1 ) ) = g ( z ( 2 ) ) a^{(2)}= g(\Theta^{(1)}a^{(1)})=g(z^{(2)}) a(2)=g(Θ(1)a(1))=g(z(2))
预测结果即: h Θ ( x ) = a ( 3 ) = g ( Θ ( 2 ) a ( 2 ) ) = g ( z ( 3 ) ) h_\Theta(x) = a^{(3)} = g(\Theta^{(2)}a^{(2)}) = g(z^{(3)}) hΘ(x)=a(3)=g(Θ(2)a(2))=g(z(3))
- 即有 z i ( j ) = Θ i , 0 ( j − 1 ) a 0 ( j − 1 ) + Θ i , 1 ( j − 1 ) a 1 ( j − 1 ) + ⋯ + Θ i , n ( j − 1 ) a n ( j − 1 ) z^{(j)}_i = \Theta^{(j-1)}_{i,0}a^{(j-1)}_{0}+ \Theta^{(j-1)}_{i,1}a^{(j-1)}_{1}+\dots+ \Theta^{(j-1)}_{i,n}a^{(j-1)}_{n} zi(j)=Θi,0(j−1)a0(j−1)+Θi,1(j−1)a1(j−1)+⋯+Θi,n(j−1)an(j−1),
- z ( j ) = Θ ( j − 1 ) a ( j − 1 ) z^{(j)} = \Theta^{(j-1)}a^{(j-1)} z(j)=Θ(j−1)a(j−1), a ( j ) = g ( z ( j ) ) a^{(j)} = g(z^{(j)}) a(j)=g(z(j)),通过该式即可计算神经网络中每一层的值。
扩展到所有样本实例:
z ( 2 ) = Θ ( 1 ) X T {{z}^{\left( 2 \right)}}={{\Theta }^{\left( 1 \right)}} {{X}^{T}} z(2)=Θ(1)XT,这时 z ( 2 ) z^{(2)} z(2) 是一个 s 2 × m s_2 \times m s2×m 维矩阵。
m m m: 训练集中的样本实例数量
s 2 s_2 s2: 第二层神经网络中激活单元的数量
我们习惯于将输入层称为神经网络的第 0 层,如上图的神经网络被称为三层网络。
4.5 例子和直观理解1(Examples and Intuitions I)
为了更好的理解神经网络,举例单层神经网络进行逻辑运算的例子。
下面的例子中, x 1 , x 2 x_1,x_2 x1,x2 为二进制数。
逻辑与(AND)运算(都为真值则结果才为真)神经网络:

Θ ( 1 ) = [ − 30 20 20 ] \Theta^{(1)} =\begin{bmatrix}-30 & 20 & 20\end{bmatrix} Θ(1)=[−302020], h Θ ( x ) = g ( − 30 + 20 x 1 + 20 x 2 ) h_\Theta(x) = g(-30+20x_1+20x_2) hΘ(x)=g(−30+20x1+20x2)。
回顾 sigmoid 函数图像,根据输入则有上图中右边的表格,即 h θ ( x ) ≈ x 1 AND x 2 h_\theta(x)\approx x_1\ \text{AND}\ x_2 hθ(x)≈x1 AND x2。这样就实现了一个能够进行与运算的神经网络。

再举一例,逻辑或(OR)运算(有一个真值则结果就为真)神经网络:
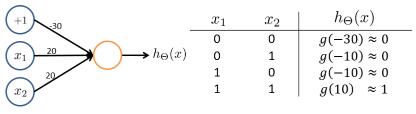
4.6 例子和直观理解2(Examples and Intuitions II)
下面逐步构建复杂一点的神经网络
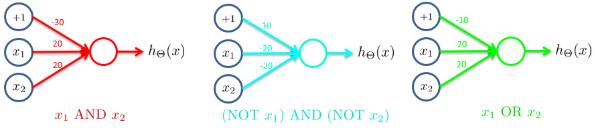
如上图,我们分别构建了三个单层神经网络,将这三个网络组合起来,可得到一个新的神经网络,其可完成逻辑运算中的异或(XNOR)操作:

这里的组合即为 XNOR = ( x 1 AND x 2 ) OR ( ( NOT x 1 ) AND ( NOT x 2 ) ) \text{XNOR}=( \text{x}_1\, \text{AND}\, \text{x}_2 )\, \text{OR} \left( \left( \text{NOT}\, \text{x}_1 \right) \text{AND} \left( \text{NOT}\, \text{x}_2 \right) \right) XNOR=(x1ANDx2)OR((NOTx1)AND(NOTx2))
Θ ( 1 ) = [ − 30 20 20 10 − 20 − 20 ] \Theta^{(1)} =\begin{bmatrix}-30 & 20 & 20 \\ 10 & -20 & -20\end{bmatrix} Θ(1)=[−301020−2020−20], Θ ( 2 ) = [ − 10 20 20 ] \Theta^{(2)} =\begin{bmatrix}-10 & 20 & 20\end{bmatrix} Θ(2)=[−102020],
a ( 2 ) = g ( Θ ( 1 ) ⋅ x ) a^{(2)} = g(\Theta^{(1)} \cdot x) a(2)=g(Θ(1)⋅x), a ( 3 ) = g ( Θ ( 2 ) ⋅ a ( 2 ) ) , h Θ ( x ) = a ( 3 ) a^{(3)} = g(\Theta^{(2)} \cdot a^{(2)}) , h_\Theta(x) = a^{(3)} a(3)=g(Θ(2)⋅a(2)),hΘ(x)=a(3)
可见,特征值能不断升级,并抽取出更多信息,直到计算出结果。而如此不断组合,我们就可以逐渐构造出越来越复杂、强大的神经网络,比如用于手写识别的神经网络。
4.7 多类别分类(Multiclass Classification)
之前讨论的都是预测结果为单值情况下的神经网络,要实现多类别分类,其实只要修改一下输出层,让输出层包含多个输出单元即可。
举一个 4 分类问题的实例:

有四种分类情况,那么就让输出层包含 4 个输出单元即可,则 h Θ h_\Theta hΘ 为 4 维向量。
神经网络中的多分类算法算是对 one-vs-all 思想的扩展,定义预测结果一共有 4 种情况:
如果预测结果 h Θ ( x ) = [ 0 0 1 0 ] h_\Theta(x) =\begin{bmatrix}0 \\ 0 \\ 1 \\ 0 \end{bmatrix} hΘ(x)=⎣⎢⎢⎡0010⎦⎥⎥⎤,那么表示 h Θ ( x ) 3 h_\Theta(x)_3 hΘ(x)3,即分为第 3 类,对应于图中的摩托车(Motorcycle)。
编程作业总结:
- max(A, [ ], 2) to obtain the max for each row.
- a == b % You should try different values of b here.
理论总结:
- 多分类问题,要分为 K K K 类,就在输出层放置 K K K 个输出单元,对于单个样本实例,预测向量 h Θ ( x ) h_\Theta(x) hΘ(x) 为 K K K 维向量,我们则依据这个预测向量,得出该实例属于哪个类 y ( i ) y^{(i)} y(i)。
- 注意,神经网络中的预测和结果都是 K K K 维向量,而不再只是一个实数了。
5. Week 5(神经网络的学习(Neural Networks: Learning))
5.1 代价函数
首先引入一些便于稍后讨论的新标记方法:
假设神经网络的训练样本有 m m m个,每个包含一组输入 x x x和一组输出信号 y y y, L L L表示神经网络层数, S l S_l