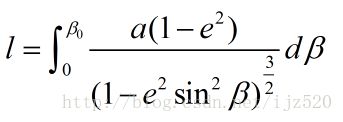MATLAB嵌套函数的应用
嵌套函数在求解积分上限中的应用
本例关于β的积分结果不能解析表达,需要数值积分来做,同时还要求一个非线性方程。代码如下:
function sol=example1(a,e,l)
function f=fun1(beta)
f=a.*(1-e.^2)./(1-e.^2*sin(beta).^2).^(3/2);
end
function g=fun2(beta0)
g=quadl(@fun1,0,beta0)-l;
end
sol=fzero(@fun2,3);
end本例采用了两个嵌套函数,fun1和fun2,fun1的功能是建立积分表达式,fun2的功能是建立关于β0的非线性方程。由于a、e和l是已知的,因此,a、e和l作为整个函数example1的输入,实际应用中给定一组a、e和l作为整个函数example1的输入。给定a=20、e=0.6和l=6,可以求解相应的解如下:
ol=example1(20,0.6,6)
sol =
0.4519嵌套函数在GUI中的应用
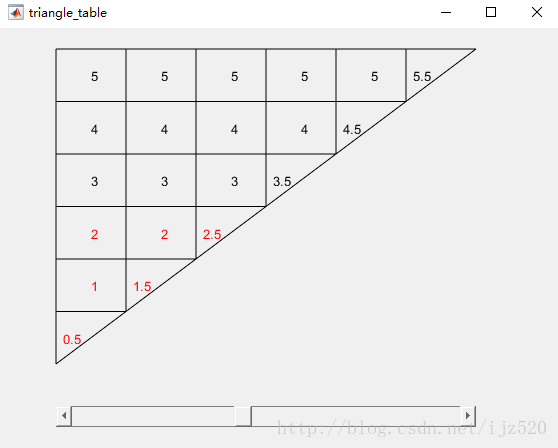
用Matlab生成一个三角形界面
要求
- 图上的数字根据行数和列数动态生成,每一层都比上面大1
- 在滚动条滚动的时候,会根据滚动条的位置,使三角形中的数字变红,最大值使数字全部变成红色,最小值使得数字全变成黑色
代码如下:
function triangle_table
fig=figure('defaultuicontrolunits','normalized','name','triangle_table',...
'numbertitle','off','menubar','none');
ah=axes('Pos',[.1 .2 .75 .75],'Visible','off');
slider_h=uicontrol('style','slider','units','normalized','pos',...
[0.1,0.05,0.75,0.05],'sliderstep',[1/6,0.05],'callback',@change_color);
hold on
for k=0:6
plot(0:6-k,(6-k)*ones(1,(7-k)),'k');
plot(k*ones(1,(7-k)),k:6,'k');
end
plot([0,6],[0,6],'k');
hold off;
for x=1:5
for y=1:x
text(y-0.5,x+0.5,num2str(x),'color','k','tag','数字');
end
end
for k=0:5
text(k+0.1,k+0.5,[num2str(k),'.5'],'tag','数字');
end
%=====slider's callback function(nested function)============
function change_color(hObject,eventdata)
v=round(6*get(slider_h,'value'));
num_h=findobj('tag','数字');
num_pos=get(num_h,'pos');
red_num_logic=cellfun(@(x)(x(1)<=v&&x(2)<=v),num_pos);
set(num_h(red_num_logic),'color','r');
set(num_h(~red_num_logic),'color','k');
end
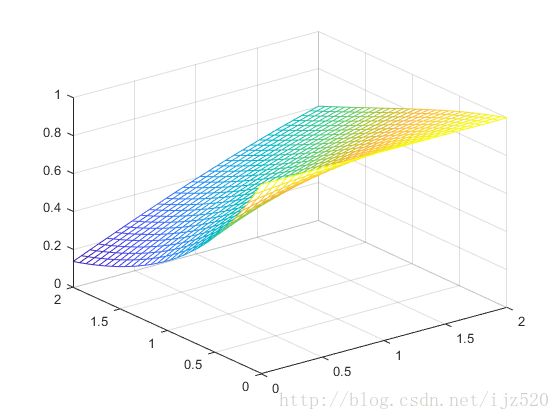
end生成的示意图
本例生成界面的思路是用plot来画线,用text函数来填格子。每次移动滚动条后,得到当前滚动条的值。根据这个值来判断究竟把那些数字设成红色那些设成黑色。slider_h是滚动条的句柄,它的回调函数change_color用嵌套函数来实现,这样,slider_h对于嵌套函数来说是可见的,不采用额外的参数传递方式来传递到回调函数内部。
嵌套函数在3D作图中的一个应用
画出下列函数的图像
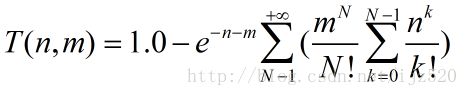
本例需要计算两个求和项,其中最外层要求一个无穷级数,分析表达式,可以得知,实际计算中,N不必取到无穷,只要取到30就可以达到较高的精度。代码如下
function [m,n,TT]=plot3dnmT(N,L)
%N:inf 的近似,L:[0,2]区间的剖分个数
C=zeros(N,1); %nested-function;Tmn=calcT(mm,nn)中用来储存计算结果
m=linspace(0,2,L);
[m,n]=meshgrid(m,m);
TT=zeros(size(n)); %和网格数据m,n对应的计算出来的T(m,n)网格数据
for ii=1:L
for jj=1:L
TT(ii,jj)=calcT(m(ii,jj),n(ii,jj));
end
end
%================计算T(m,n)的nest-function
function Tmn=calcT(mm,nn)
for N1=1:N
C(N1)=(mm^N1/gamma(N1+1))*sum(nn.^(0:N1-1)./gamma(1:N1));
Tmn=1.0-exp(-mm-nn)*sum(C);
end
end
mesh(n,m,TT)
end嵌套函数表示待优化的目标函数
求下面表达式的最小值
已知w=[π/2,π,3π/2];N=[π/2-1,-2,-3π/2-1]
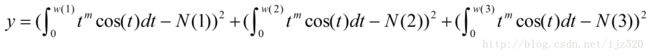
其中,m在[0,2]范围内
代码如下:
function m=Findm
w=[pi/2,pi,pi*1.5];
N=[pi/2-1,-2,-1.5*pi-1];
function y=ObjectFun(m)
y=(quadl(@(t)t.^m.*cos(t),0,w(1))-N(1))^2+...
(quadl(@(t)t.^m.*cos(t),0,w(2))-N(2))^2+...
(quadl(@(t)t.^m.*cos(t),0,w(3))-N(3))^2;
end
m=fminbnd(@ObjectFun,0,2);
end上述代码中,目标函数即y用嵌套函数ObjectFun来表示。fminbnd第一个输入参数就是ObjectFun的句柄,第二第三个参数是求解最小值的范围。运行后得到结果如下:
>> format long
>> m=Findm
m =
1.000000256506471嵌套函数在表示微分方程方面的应用
求下面的微分方程在[0,5]范围的解
y″+4y=3sin(at)
其中,a是参数,初始条件为:y(0)=1,y′(0)=0。
本例要想应用matlab的微分方程求解函数ode45求解,需要改变一下形式,即变成一阶微分方程式的形式:
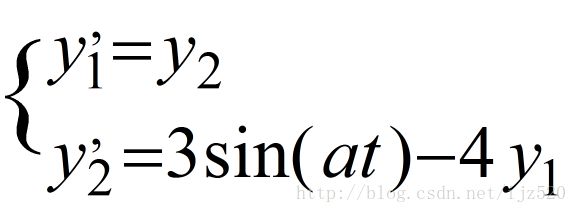
其中y₁(t)对应于函数y(t),而y₂=y′(t).
代码如下:
function example5(a)
tspan=[0,5]; %变量求解区间
y0=[1,0]; %初始值
[t,y]=ode45(@tfys,tspan,y0) %调用ode45求解方程
figure;
plot(t,y(:,1),'k-'); %画函数y(t)的曲线
hold on;
plot(t,y(:,2),'k:'); %画函数y(t)导数的曲线
set(gca,'fontsize',12); %设置当前坐标轴字体大小
xlabel('\itt','fontsize',16); %标注x轴
ylabel('\ity','fontsize',16); %标注y轴
%用嵌套函数定义微分方程组
function dy=tfys(t,y)
dy(1,1)=y(2); %对应于粒子中方程组的第一个方程
dy(2,1)=3*sin(a*t)-4*y(1); %对应于例子中方程组第二个方程
end
end