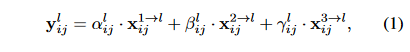【CV中的特征金字塔】一,工程价值极大的YOLOv3-ASFF
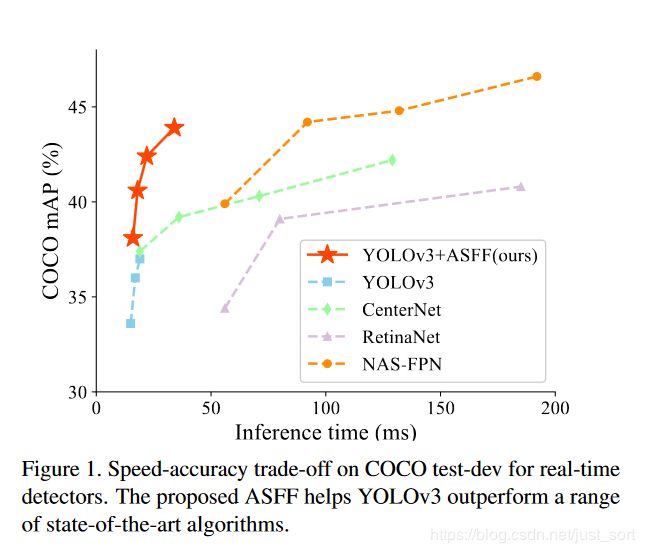
下面先放一张论文的结果图。。
1. 前言
今天为大家介绍一下2019年的一篇论文 《Learning Spatial Fusion for Single-Shot Object Detection》,这篇论文主要是因为其提出的 自适应空间特征融合 (ASFF)被大家所熟知。金字塔特征表示法(FPN)是解决目标检测尺度变化挑战的常用方法。但是,对于基于FPN的单级检测器来说,不同特征尺度之间的不一致是其主要限制。因此这篇论文提出了一种新的数据驱动的金字塔特征融合方式,称之为自适应空间特征融合(ASFF)。它学习了在空间上过滤冲突信息以抑制梯度反传的时候不一致的方法,从而改善了特征的比例不变性,并且推理开销降低。借助ASFF策略和可靠的YOLOV3 BaseLine,在COCO数据集上实现了45FPS/42.4%AP以及29FPS/43.9%AP。论文原文以及代码链接见附录。
2. 一个更强的YOLOV3基准
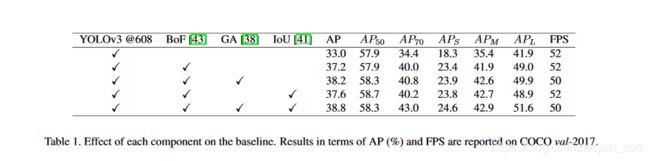
这篇文章之所以取得这么好的效果不仅仅是因为它提出的ASFF这种特征自适应融合方式,论文在YOLOV3的基础上集百家之长,构建了一个非常强的YOLOV3 BaseLine,这个BaseLine在MSCOCO上的mAP就达到了38.8%。相比于原始的YOLOV3的33%,提升了接近6个点。。论文使用的技巧包括:
- Guided Anchoring
- Bag of Tricks
- Additional IoU Loss
3. 自适应特征融合(ASFF)
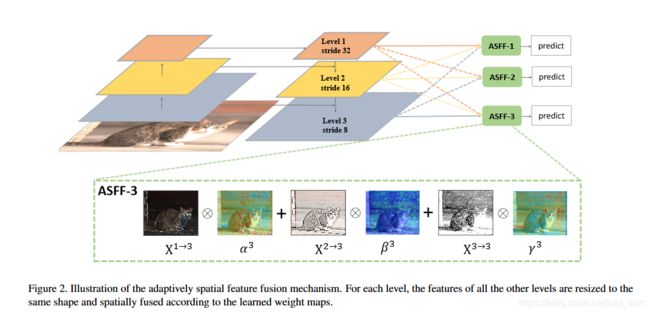
为了更加充分的利用高层特征的语义信息和底层特征的细粒度特征,很多网络都会采用FPN的方式输出多层特征,但是无论是类似于YOLOv3还是RetinaNet,它们都多用concatenation或者element-wise这种直接衔接或者相加的方式,论文认为这样并不能充分的利用不同尺度的特征,所以提出了Adaptively Spatial Feature Fusion(自适应特征融合方式)。以ASFF-3为例,其结构可以表示为Figure2。
在Figure2中,绿色框描述了如何将特征进行融合,其中 X 1 , X 2 , X 3 X^1,X^2,X^3 X1,X2,X3分别为来自level1,level2,level3这三个层的特征。然后level1,level2,level3这三个层的特征分别乘上权重参数 α 3 , β 3 , γ 3 \alpha^3,\beta^3,\gamma^3 α3,β3,γ3并求和,就可以得到新的融合后的特征ASFF-3。这个过程可以用公式(1)来表示:
因此这里是相加的操作,所以需要加的时候必须保证leve1,level2,level3输出的特征相同,且通道数也要相同,所以需要对不同的特征层做上采样或者下采样并调整通道数来满足条件。对于需要上采样的层,如想得到ASFF3,需要将level1的特征图调整到和level3的特征图尺寸一致,采用的方式是先通过 1 × 1 1\times 1 1×1卷积调整到和level3通道数一致,再用插值的方式将尺寸调整到一致。而对于需要下采样的层,比如想得到ASFF1,对于level2的特征图到level1的特征图只需要用一个 3 × 3 3\times 3 3×3并且 s t r i d e = 2 stride=2 stride=2的卷积就OK了,如果是level3的特征图到level1的特征图则需要在 3 × 3 3\times 3 3×3卷积的基础上再加上一个 s t r i d e = 2 stride=2 stride=2的最大池化层。
对于权重参数 α \alpha α, β \beta β, γ \gamma γ,则是通过resize后的level1~level3特征图经过 1 × 1 1\times 1 1×1卷积获得的。并且参数 α \alpha α, β \beta β, γ \gamma γ经过 c o n c a t concat concat之后通过softmax使得它们的范围都在[0,1]并且和为1。
4. ASFF的可解释性
论文通过梯度和反向传播来解释为什么ASFF会有效。论文以YOLOv3为例,加入FPN后通过链式法则我们可以知道在反向传播的时候梯度计算如公式(3)所示:
稍微解释一下,左边的第一项 ∂ L ∂ x i j 1 \frac{\partial L}{\partial x_{ij}^1} ∂xij1∂L代表的是损失函数对level1的特征图的某个像素求导,在YOLOV3中不同尺度的层之间的尺度变化一般就是下采样和上采样,因此 ∂ x i j 1 − > l ∂ x i j 1 \frac{\partial x_{ij}^{1->l}}{\partial x_{ij}^1} ∂xij1∂xij1−>l这一项通常为固定值,为了简化表示我们可以设置为1,即: ∂ x i j 1 − > l ∂ x i j 1 ≈ 1 \frac{\partial x_{ij}^{1->l}}{\partial x_{ij}^1}\approx 1 ∂xij1∂xij1−>l≈1,那么公式(3)可以简化为公式(4):
进一步, ∂ y i j 1 ∂ x i j 1 \frac{\partial y_{ij}^1}{\partial x_{ij}^1} ∂xij1∂yij1这一项相当于对输出特征的activation操作,导数也将为固定值, ∂ y i j l ∂ x i j 1 − > l \frac{\partial y_{ij}^l}{\partial x_{ij}^{1->l}} ∂xij1−>l∂yijl,所以我们可以将它的值同样简化为1,则表达式进一步简化成了公式(5):
假设 l e v e l 1 ( i , j ) level1(i,j) level1(i,j)对应特征图位置刚好有物体并且为正样本,那其他 l e v e l level level上对应的 ( i , j ) (i,j) (i,j)位置上就可能刚好为负样本,这样反向传播的梯度中既包含了正样本又包含了负样本,这种不连续性会对梯度结果造成干扰,并且降低训练的效率。而通过ASFF的方式,反向传播的梯度表达式就变成了(6):
因此,如果出现刚才的情况我们可以通过将 α 2 \alpha^2 α2和 α 3 \alpha^3 α3设置为0来解决,因为这样负样本的梯度不会结果造成干扰。
同时这也解释了为什么特征融合的权重参数来源于输出特征+卷积,因为融合的权重参数和特征是息息相关的。
5. 实验结果
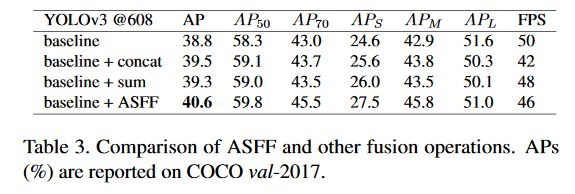
下面的Table3展示了ASFF相比于concat和sum的方式的结果,可以看到加入了ASFF在BaseLine的基础上提升了2个多个mAP。
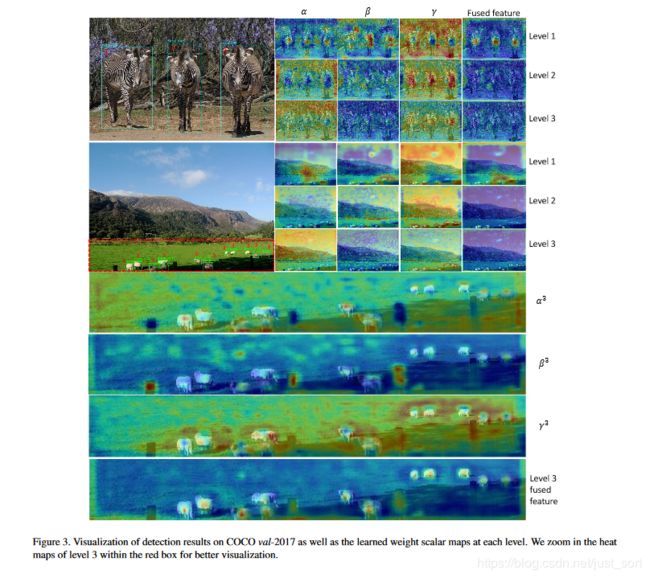
接着作者又对ASFF做了可视化分析,如Figure3所示。
可视化的结果进一步解释了ASFF的有效性。比如对于斑马的检测,可以看到斑马实际上是在level1这个特征图上被检测到的(响应越大,heatmap越红),并且观察level1这一层的 α \alpha α, β \beta β, γ \gamma γ的权重可以发现,对于图中斑马这种大目标更容易被高层的特征捕捉到,因为对于大物体我们需要更大的感受野和高级语义特征。而对于下面的羊群的检测来讲,可以看到羊更多的是被level2和level3检测到,这也说明了对于小物体,我们更需要底层特征中的细粒度特征来辨别。
6. 结论
这篇论文将YOLOv3的结果做得非常好,是具有很大的工程实践意义的,论文具体是具体如何做出的Stronger YOLOv3 BaseLine,我相信有不少小伙伴和我一样感兴趣。这个可以去源码一探究竟了。这是近几个月最喜欢的一篇论文了,不仅仅是因为它的精度非常强,而且从数学角度来简洁的说明这个方法的有效性也是棒的。
7. 参考
- 论文原文:https://arxiv.org/pdf/1911.09516.pdf
- 源码:https://github.com/ruinmessi/ASFF
- 参考:https://blog.csdn.net/watermelon1123/article/details/103277773
- Guided Anchoring:Jiaqi Wang, Kai Chen, Shuo Yang, Chen Change Loy, andDahua Lin. Region proposal by guided anchoring. InCVPR,2019.
- Bag of Freebies for Training Object Detection Neural Networks : https://arxiv.org/abs/1902.04103
欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享,坚持原创,每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题,或者想要加入交流群,欢迎添加BBuf微信:
![]()