数学规划

优化问题的三要素：

• 决策变量
• 目标函数
• 约束条件

类型有：
连续优化：

• 线性规划（LP）：目标和约束函数均为线性函数
• 非线性规划（NLP）：目标或约束中存在非线性函数
  
  • 二次规划（QP）：目标为二次函数，约束为线性函数

离散优化：

• 整数规划（IP）：决策变量（全部或部分）为整数
  
  • 整数线性规划（ILP）， 整数非线性规划（INLP）
  • 纯整数规划（PIP），混合整数规划（MIP）
  • 一般整数规划，0-1规划

目标规划的求解思路：
1.加权系数法：
为每一个目标赋一个权系数，把多目标模型转化为单一目标的模型。
2.优先等级法：
将各目标按其重要程度不同的优先等级，转化为单目标模型。

---

线性规划：

只能解决一组线性约束条件，一个目标的最大或最小值的问题。

线性规划模型的构成：

1.变量：

• 决策变量：表示具体生产活动的变量。
• 补充变量：松弛变量、剩余变量、人工变量

2.约束条件：
对变量的限制条件，又分为：

• 结构约束条件
• 非负约束条件

3.目标函数：
它是优化的取向、评价方案优劣的指标。
具体的线性规划模型中优化的取向只有最大化max和最小化min

LP模型的一般形式为：

MAX(MIN) Z=c1x1+c2x2+...+cnxn

s.t=⎧⎩⎨⎪⎪⎪⎪⎪⎪a11x1+a12x2+...+a1nxn<=(=,>=)b1am1x1+am2x2+...+amnxn<=(=,>=)bmx1,x2,...,xn>=0

标准形式为：
Max Z=CX
s.t=⎧⎩⎨AX=bX>=0

在作原理性分析时，常用以下两种形式表示线性规划模型 maxz= ∑nj=1cjxj ：

1.和式形式：
s.t=⎧⎩⎨∑nj=1aijxj=bi,xj>=0, i = 1,2,...,m j = 1,2,...,m

2.矩形形式：略。

一般采用和式形式。

线性规划解的基本概念：

Max Z=CX
s.t=⎧⎩⎨AX=bX>=0

设 r(A)=m(n>m) 。则 A 中任一个m阶可逆阵 B 称为线性规划问题中一个基矩阵，简称基。

若记 B=[p1,p2,...,pm] ，则称
pj(j=1,2,...,m) 为基 B 中的一个基向量。
与基向量 pj 对应的变量 xj 称为基变量 xj 。
而 A 中其余 n−m 列向量称为非基向量。
与非基向量对应的变量为非基变量。

解的类别：
1.可行解：满足线性规划所有约束条件的变量的一组取值。
2.最优解：是目标函数达到最优解的可行解。
3.基本解：在约束方程组系数矩阵中找到一个基，令这个基的非基变量为零，再求解这个m元线性方程组就可得到唯一的解。

---

练习题：
SAILCO公司需要决定下四个季度的帆船生产量。下四个季度的帆船需求量分别是40条，60条，75条，25条，这些需求必须按时满足。每个季度正常的生产能力是40条帆船，每条船的生产费用为400美元。如果加班生产，每条船的生产费用为450美元。每个季度末，每条船的库存费用为20美元。假定生产提前期为0，初始库存为10条船。如何安排生产可使总费用最小？

分析：
用DEM,RP,OP,INV分别表示需求量、正常生产的产量、加班生产的产量、库存量，则DEM,RP,OP,INV对每个季度都应该有一个对应的值，也就说他们都应该是一个由4个元素组成的数组，其中DEM是已知的，而RP,OP,INV是未知数。

目标函数是所有费用的和： MIN=∑I=1,2,3,4400RP(I)+450OP(I)+20INV(I)
约束条件有两个：
(1). RP(I)<40
(2). INV(I)=INV(I−1)+RP(I)+OP(I)−DEM(I) and INV(0)=10

代码如下：

sets:
quarters/1..4/:DEM, RP, OP, INV;
endsets
    min = @sum(quarters:400*RP+450*OP+20*INV);
    @for(quarters:RP<40);
    @for(quarters(I)|I#GT#1:INV(I) = INV(I-1) + RP(I) + OP(I) - DEM(I));
    INV(1) = 10 + RP(1) + OP(1) - DEM(1);
data:
    DEM = 40, 60, 75, 25;
enddata

结果如下：

---

线性规划的对偶问题

1.提出和模型：
比如煤电油问题，原问题是已知消耗量，求总收入最大，这个问题的变量是消耗量。现如果要求另有厂要购买煤电油，在原厂可接受条件下，单价多少可使另厂付费最低，而此时问题的变量变成了价格。

2.原问题与对偶问题的对应关系：

原问题（P）：
Max Z=CX
s.t=⎧⎩⎨AX<=bX>=0

对偶问题（D）：
Min W=bTY
s.t=⎧⎩⎨ATY>=CTY>=0

则煤电油例子的原问题和对偶问题的对应关系是：

原问题（P）	对偶问题（D）
目标MAX型	目标MIN型
有n个变量（非负）	有n个约束（大于等于）
有m个约数（小于等于）	有m个变量（非负）
价格系数	资源向量
资源向量	价格系数
技术系数矩阵	技术系数矩阵的转置。

---

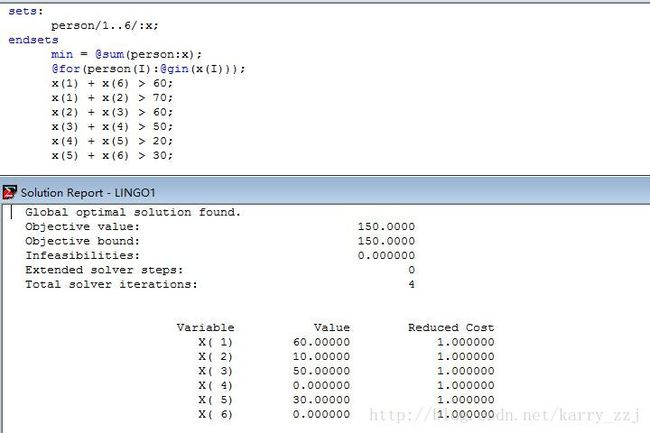
整数规划（IP）

一般模型：

Max Z=CX
s.t=⎧⎩⎨⎪⎪⎪⎪⎪⎪AX=bX>=0X为整数

解法：分枝定界法或割平面法。基本思想就是把一个整数规划问题化为一系列的线性规划问题来求解。

分类：

• 纯整数规划：所有变量限制为整数。
• 混合整数规划：仅部分变量限制为整数。
• 0-1整数规划：变量的取值仅限于0或1。

举例：