Codeforces Round #226 (Div. 2) ABC

晚了一个小时去做题，，，Ａ了前两道。

A. Bear and Raspberry

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

The bear decided to store some raspberry for the winter. He cunningly found out the price for a barrel of honey in kilos of raspberry for each of the following n days. According to the bear's data, on the i-th (1 ≤ i ≤ n) day, the price for one barrel of honey is going to is xi kilos of raspberry.

Unfortunately, the bear has neither a honey barrel, nor the raspberry. At the same time, the bear's got a friend who is ready to lend him a barrel of honey for exactly one day for c kilograms of raspberry. That's why the bear came up with a smart plan. He wants to choose some day d (1 ≤ d < n), lent a barrel of honey and immediately (on day d) sell it according to a daily exchange rate. The next day (d + 1) the bear wants to buy a new barrel of honey according to a daily exchange rate (as he's got some raspberry left from selling the previous barrel) and immediately (on day d + 1) give his friend the borrowed barrel of honey as well as c kilograms of raspberry for renting the barrel.

The bear wants to execute his plan at most once and then hibernate. What maximum number of kilograms of raspberry can he earn? Note that if at some point of the plan the bear runs out of the raspberry, then he won't execute such a plan.

Input

The first line contains two space-separated integers, n and c (2 ≤ n ≤ 100, 0 ≤ c ≤ 100), — the number of days and the number of kilos of raspberry that the bear should give for borrowing the barrel.

The second line contains n space-separated integers x1, x2, ..., xn (0 ≤ xi ≤ 100), the price of a honey barrel on day i.

Output

Print a single integer — the answer to the problem.

Sample test(s)

input

5 1
5 10 7 3 20

output

3

input

6 2
100 1 10 40 10 40

output

97

input

3 0
1 2 3

output

0

Note

In the first sample the bear will lend a honey barrel at day 3 and then sell it for 7. Then the bear will buy a barrel for 3 and return it to the friend. So, the profit is (7 - 3 - 1) = 3.

In the second sample bear will lend a honey barrel at day 1 and then sell it for 100. Then the bear buy the barrel for 1 at the day 2. So, the profit is (100 - 1 - 2) = 97.

ＫＥＹ

In this task required to understand that the answer max(a[i] - a[i - 1] - c),i = 2..n and don't forget that the answer not negative as Bear can not borrow in the debt barrel of honey.

读题小有困难，读完题发现就是一个公式。

#include 
using namespace std;
int a[101],maxn=0,n,c,i,j;
int main()
{
	cin>>n>>c; cin>>a[0];
	for (i=1;i>a[i];
		j=a[i-1]-a[i];
		maxn=j>maxn?j:maxn;
	}
	if (maxn-c>0) cout<

B. Bear and Strings

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

The bear has a string s = s1s2... s|s| (record |s| is the string's length), consisting of lowercase English letters. The bear wants to count the number of such pairs of indices i, j (1 ≤ i ≤ j ≤ |s|), that string x(i, j) = sisi + 1... sj contains at least one string "bear" as a substring.

String x(i, j) contains string "bear", if there is such index k (i ≤ k ≤ j - 3), that sk = b, sk + 1 = e, sk + 2 = a, sk + 3 = r.

Help the bear cope with the given problem.

Input

The first line contains a non-empty string s (1 ≤ |s| ≤ 5000). It is guaranteed that the string only consists of lowercase English letters.

Output

Print a single number — the answer to the problem.

Sample test(s)

input

bearbtear

output

6

input

bearaabearc

output

20

Note

In the first sample, the following pairs (i, j) match: (1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (1, 9).

In the second sample, the following pairs (i, j) match: (1,  4), (1,  5), (1,  6), (1,  7), (1,  8), (1,  9), (1,  10), (1,  11), (2,  10), (2,  11), (3,  10), (3,  11), (4,  10), (4,  11), (5,  10), (5,  11), (6,  10), (6,  11), (7,  10), (7,  11).

KEY

In this problem you could write a better solution than the naive. To do this, you can iterate through the first cycle of the left index lconsidered substring and the second cycle of the right index r considered substring (l ≤ r). If any position has been substring "bear", means all the strings x(l, j) (i ≤ j), also contain "bear" as a substring. So we can add to the answer |s| - j + 1 and exit from the second cycle. Also needed to understand, that if the string x(l, j) was not a substring "bear", then in row x(l, j + 1) substring "bear" could appear only in the last four characters.

一个字符串究竟有多少个包含“bear”的字串呢？我匹配用的是kmp

#include 
using namespace std;
string s1,s2="bear";
int l1,l2=4,i,j,n,lasti=0;
int main()
{
	cin>>s1;
	l1=s1.size();	
	j=-1; int ans=0;
	for (i=0;i-1 && s1[i]!=s2[j+1]) j=-1;
		if (s1[i] == s2[j+1]) ++j;
		if (j+1==l2){
		//	cout<

C. Bear and Prime Numbers

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Recently, the bear started studying data structures and faced the following problem.

You are given a sequence of integers x1, x2, ..., xn of length n and m queries, each of them is characterized by two integers li, ri. Let's introduce f(p) to represent the number of such indexes k, that xk is divisible by p. The answer to the query li, ri is the sum: , where S(li, ri) is a set of prime numbers from segment [li, ri] (both borders are included in the segment).

Help the bear cope with the problem.

Input

The first line contains integer n (1 ≤ n ≤ 106). The second line contains n integers x1, x2, ..., xn (2 ≤ xi ≤ 107). The numbers are not necessarily distinct.

The third line contains integer m (1 ≤ m ≤ 50000). Each of the following m lines contains a pair of space-separated integers, li and ri (2 ≤ li ≤ ri ≤ 2·109) — the numbers that characterize the current query.

Output

Print m integers — the answers to the queries on the order the queries appear in the input.

Sample test(s)

input

6
5 5 7 10 14 15
3
2 11
3 12
4 4

output

9
7
0

input

7
2 3 5 7 11 4 8
2
8 10
2 123

output

0
7

Note

Consider the first sample. Overall, the first sample has 3 queries.

1. The first query l = 2, r = 11 comes. You need to count f(2) + f(3) + f(5) + f(7) + f(11) = 2 + 1 + 4 + 2 + 0 = 9.
2. The second query comes l = 3, r = 12. You need to count f(3) + f(5) + f(7) + f(11) = 1 + 4 + 2 + 0 = 7.
3. The third query comes l = 4, r = 4. As this interval has no prime numbers, then the sum equals 0.

KEY

In order to solve given problem, contestant should solve several subproblems :

1) First one is to compute amount of entries of each natural number between 2 and 107 in given list. This subproblem can be solved by creating array count of 107 elements and increasing corresponding element when scanning input.

2) Second one is to compute f(n).

First of all, we need to find all primes less than 107 and then for each prime n compute f(n).

How to compute f(2)? We should sum count[2],count[4],count[6],count[8],...

How to compute f(5)? We should sum count[5],count[10],count[15],count[20],...

How to compute f(n)? We should sum count[n],count[2·n],count[3·n],count[4·n],...

It can be seen that given algo is very similar to Sieve of Eratosthenes. (Info here http://e-maxx.ru/algo/eratosthenes_sieve) So we can use this algo if we change it a little bit. Also, we will store results of calculation in array, e.g. pre. Namely, pre[n] = f(n).

3) Now we can calculate partial sums of pre array. It can be made in a single pass just adding pre[i - 1] to pre[i].

4) If we know partial sums of array then we can calculate sum of array elements between l and r in time proportional O(1), just calculatepre[r] - pre[l - 1].

5) Now we can read queries and immediately response to them. You shouldn't forget that right boundaries of intervals can be greater than107, so you can always decrease it to 107, because all numbers in given list are less than 107.

//待补坑

这道题的处理方法非常的巧妙。如果不注意方法，题目会非常难写

#include 
using namespace std;

const int MAXN=10000001;
int vis[MAXN]={0},sum[MAXN]={0},v[MAXN]={0},num,n,i,j,m,l,r;
 
int main()
{
	cin>>n;
	for (i=0;i>num;
		vis[num]++;
	}
	for (i=2;i>m;
	for (i=0;i>l>>r;
		if (r>=MAXN) r=MAXN-1;
		if (l>=MAXN) l=MAXN;;
		cout<

D. Bear and Floodlight

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

One day a bear lived on the Oxy axis. He was afraid of the dark, so he couldn't move at night along the plane points that aren't lit. One day the bear wanted to have a night walk from his house at point (l, 0) to his friend's house at point (r, 0), along the segment of length (r - l). Of course, if he wants to make this walk, he needs each point of the segment to be lit. That's why the bear called his friend (and yes, in the middle of the night) asking for a very delicate favor.

The Oxy axis contains n floodlights. Floodlight i is at point (xi, yi) and can light any angle of the plane as large as ai degree with vertex at point (xi, yi). The bear asked his friend to turn the floodlights so that he (the bear) could go as far away from his house as possible during the walking along the segment. His kind friend agreed to fulfill his request. And while he is at it, the bear wonders: what is the furthest he can go away from his house? Hep him and find this distance.

Consider that the plane has no obstacles and no other light sources besides the floodlights. The bear's friend cannot turn the floodlights during the bear's walk. Assume that after all the floodlights are turned in the correct direction, the bear goes for a walk and his friend goes to bed.

Input

The first line contains three space-separated integers n, l, r (1 ≤ n ≤ 20;  - 105 ≤ l ≤ r ≤ 105). The i-th of the next n lines contain three space-separated integers xi, yi, ai ( - 1000 ≤ xi ≤ 1000; 1 ≤ yi ≤ 1000; 1 ≤ ai ≤ 90) — the floodlights' description.

Note that two floodlights can be at the same point of the plane.

Output

Print a single real number — the answer to the problem. The answer will be considered correct if its relative or absolute error doesn't exceed 10 - 6.

Sample test(s)

input

2 3 5
3 1 45
5 1 45

output

2.000000000

input

1 0 1
1 1 30

output

0.732050808

input

1 0 1
1 1 45

output

1.000000000

input

1 0 2
0 2 90

output

2.000000000

Note

In the first sample, one of the possible solutions is:

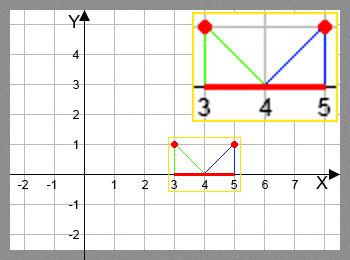
In the second sample, a single solution is:

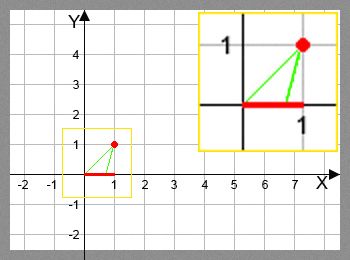
In the third sample, a single solution is:

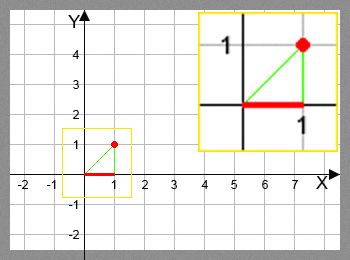
KEY

In this task, it is crucial to understand that whether there is lighted part of road with length dist then next part should be lit in a such way that leftmost lighted point is touching with dist.

Let's suppose that road is lit from l to d. How we can find rightmost point on X axis that would be lit by next floodlight?

We can just use concepts of vector and rotation matrix.

Let's find vector (dx, dy) from floodlight to point on X axis (d, 0). (dx, dy) = (d - x, 0 - y).

Next point to rotate vector by angle degrees. We can use rotation matrix for this purpose.

(dx, dy) = (dx·cos(angle) - dy·sin(angle), dx·sin(angle) + dy·cos(angle))

Next, we should make second component dy of (dx, dy) equal to 1 by multiplying on coefficient k.

Now we can determine rightmost lighted point of X axis. It is x - y·dx.

You shouldn't forget that there is possibility for rightmost point to be infinitely far point.

From now on we can forget about geometry in this task.

Let's find fast way to determine optimal order of floodlights.

To achieve this goal, we can use dynamic programming approach. Namely, let's calculate answer for subsets of floodlights. Each subset would be represented as integer where k bit would be 1 if k floodlight is presented in subset and 0 if it is not, i.e. so named binary mask.

For example, dp[6] — (6 — 1102) is optimal answer for subset from 2 and 3 floodlight.

Now, let's look through subsets i in dp[i]. In subset i let's go through absent floodlights j and update result for subset where j floodlight is present, i.e. dp[ i or 2j ] = max(dp[ i or 2j], dp[ i ] + calc_rightmost_lighted_point() ). As we can calculate rightmost lighted point, so updating of answer shouldn't be a problem.

//待补坑

E. Bear in the Field

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Our bear's forest has a checkered field. The checkered field is an n × n table, the rows are numbered from 1 to n from top to bottom, the columns are numbered from 1 to n from left to right. Let's denote a cell of the field on the intersection of row x and column y by record(x, y). Each cell of the field contains growing raspberry, at that, the cell (x, y) of the field contains x + y raspberry bushes.

The bear came out to walk across the field. At the beginning of the walk his speed is (dx, dy). Then the bear spends exactly t seconds on the field. Each second the following takes place:

• Let's suppose that at the current moment the bear is in cell (x, y).
• First the bear eats the raspberry from all the bushes he has in the current cell. After the bear eats the raspberry from k bushes, he increases each component of his speed by k. In other words, if before eating the k bushes of raspberry his speed was (dx, dy), then after eating the berry his speed equals (dx + k, dy + k).
• Let's denote the current speed of the bear (dx, dy) (it was increased after the previous step). Then the bear moves from cell (x, y) to cell (((x + dx - 1) mod n) + 1, ((y + dy - 1) mod n) + 1).
• Then one additional raspberry bush grows in each cell of the field.

You task is to predict the bear's actions. Find the cell he ends up in if he starts from cell (sx, sy). Assume that each bush has infinitely much raspberry and the bear will never eat all of it.

Input

The first line of the input contains six space-separated integers: n, sx, sy, dx, dy, t (1 ≤ n ≤ 109; 1 ≤ sx, sy ≤ n;  - 100 ≤ dx, dy ≤ 100; 0 ≤ t ≤ 1018).

Output

Print two integers — the coordinates of the cell the bear will end up in after t seconds.

Sample test(s)

input

5 1 2 0 1 2

output

3 1

input

1 1 1 -1 -1 2

output

1 1

Note

Operation a mod b means taking the remainder after dividing a by b. Note that the result of the operation is always non-negative. For example, ( - 1) mod 3 = 2.

In the first sample before the first move the speed vector will equal (3,4) and the bear will get to cell (4,1). Before the second move the speed vector will equal (9,10) and he bear will get to cell (3,1). Don't forget that at the second move, the number of berry bushes increased by 1.

In the second sample before the first move the speed vector will equal (1,1) and the bear will get to cell (1,1). Before the second move, the speed vector will equal (4,4) and the bear will get to cell (1,1). Don't forget that at the second move, the number of berry bushes increased by 1.

KEY

In this task there are several problems that should be concerned:

1) Simple modeling of bear movement would cause TLE due to t  ≤  1018.

2) Task can't be solved by separating x and y axes because x and y depends on each other.

3) Also, we can't use standart method of cycle finding via modeling for a short time and checking on collisions because coordinates limitations are very large.

Let's say we have matrix (xi, yi, dxi, dyi, ti, 1).

If we multiply previous matrix by following matrix long long base[6][6] = {

{2,1,1,1,0,0},

{1,2,1,1,0,0},

{1,0,1,0,0,0},

{0,1,0,1,0,0},

{0,0,1,1,1,0},

{0,0,2,2,1,1} };

we will have get parameters on next step.

Where did the matrix? Let us write out how to change parameters with each step and see the similarity matrix.

x = 2·x + 1·y + 1·dx + 0·dy + 0·t + 0·1.

y = 1·x + 2·y + 0·dx + 1·dy + 0·t + 0·1.

dx = 1·x + 1·y + 1·dx + 0·dy + 1·t + 2·1.

dy = 1·x + 1·y + 0·dx + 1·dy + 1·t + 2·1.

t = 0·x + 0·y + 0·dx + 0·dy + 1·t + 1·1.

1 = 0·x + 0·y + 0·dx + 0·dy + 0·t + 1·1.

So if we calculate t - 1 power of base and then multiply (sx, sy, dx, dy, t, 1) by it we will calculate parameters at moment t.

Power of matrix can be calculated via binary power modulo algo due to associativity of matrix multiplication. More info at http://e-maxx.ru/algo/binary_pow

Using trivial matrix multiplication algo we will solve this task in time proportional 63·log(t).

//待补坑

kdwycz的网站：  http://kdwycz.com/

kdwyz的刷题空间：http://blog.csdn.net/kdwycz