拉普拉斯网格变形

拉普拉斯网格变形是CAGD中比较重要也是比较基础的一个技术。所以要学习三维重建相关的知识。这个拉普拉斯操作是比较基础也是一个重要的入门操作。这篇文章主要参考《Laplacian Surface Editing》这篇论文。
这里我就不翻译这篇论文了，我把其中一些重要的知识点说清楚就好了。具体相关实现代码也会在后续弄完以后放出来。这篇文章只是介绍一些简单的问题。这样再看后面的文章就容易了。
在3维数据处理中Surface Editing操作首先要保证的就是编辑之后网格的几何特征不能发生变化。打个比喻你不能在编辑人脸的时候编辑完了眼睛跑到嘴那里了。这样的编辑就是没有效果的。在保留几何细节的情况下使用微分坐标来进行编码和解码相关的网格模型。那么问题来了什么叫微分坐标呢？为什么要使用微分坐标，为什么又加拉普拉斯，怎么使用微分坐标来对整个网格进行编辑。这篇文章我主要也就解答这几个问题。当然《Laplacian Surface Editing》这篇论文中还有很多比较有趣也是一些其他的问题。比如变形之后形状发生了改变。要怎么保证形状发生改变之类的问题。这些问题我会在后面的文章中再详细说明一些。
那么现在回答第一个问题什么叫微分坐标。
其实微分坐标就是拉普拉斯算子在网格上作用所得到的结果（基于微分坐标的morphing）
这个结果是

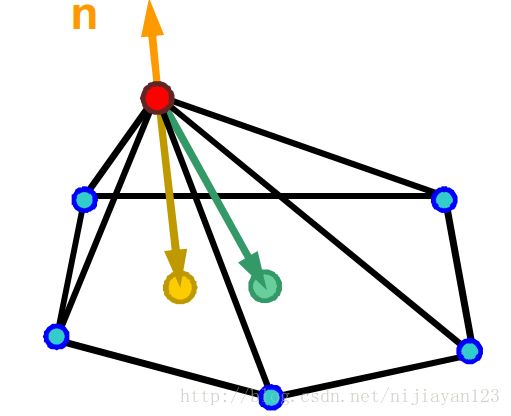
δ=Δd(vi)=1di∑j∈N(i)(vi−vj)

如果 δ=0 表示 vi 点与所有与其一环邻居点共面。
什么是拉普拉斯算子呢？
在微分几何中，曲面被描述为场，而网格又是离散化的曲面，可以看成是包含了有限个点的离散场。网格上的每个点对其周围的邻居点都是有影响。首先介绍一个拉普拉斯方程。拉普拉斯方程式一个二阶偏微分方程
∂2f∂2x2+∂2f∂2y2+∂2f∂2z2=0
其中 f(x,y,z) 是三维欧式空间的二次可微函数，上述公式相当于寻找曲线的拐点。曲面的二阶微分描述了曲面的曲率。通常描述为 Δf=∇2=0 或者 div(grad(f))=0 .通常情况下我们称 Δ 为拉普拉斯算子。
根据微分几何知识我们知道，平均法曲率向量还可以表示为如下的曲线积分的极限

K(vi)=lim|γ|→01|γ|=∫i∈γ(vi−v)dl(v)

其中， γ 是曲面上绕点 vi 的任意封闭曲线所围成的面积。对上述离散化我们可以得到拉普拉斯算子 Δd

Δd(vi)=1di∑j∈N(i)(vi−vj)

其中 N(i)={vj|vjvi∈E}
di=1|N(i)|
|N(i)| 表示 N(i) 中所含的元素的个数，称为 di 为顶点的度。
对上述式子进行改进，进而可以得带微分坐标权值选取的方案

δ=(δix,δiy,δiz)=vi−∑j∈N(i)wijVj=∑j∈N(i)wij(vi−vj)

∑j∈N(i)wij=1

令 wij=dii=1|N(i)|
这里我们可以发现微分坐标就是拓扑微分坐标。当然这里的权重的选择还有不同的选择方法。
这里可以发现微分坐标因为是根据一环邻居点之间的关系所以它保留了网格的几何信息。

下面介绍一下如何使用微分坐标进行网格的操作。
先介绍一下微分坐标相关的性值。也就是这些性值才保证了网格变形时可以使用拉普拉斯坐标。（参考 拉普拉斯坐标在网格变形中的应用研究）
(1)与线性泛函可以交换
若A是点集V的线性变换，则
A(L(vi))=L(A(vi))
(2)具有平移不变性

∑jinN(i)wij(Tvi−Tvj)=∑jinN(i)wijT(vi−vj)=∑jinN(i)wijT⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪xvi−xvjyvi−yvjzvi−zvj0⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪=∑jinN(i)wij⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪xvi−xvjyvi−yvjzvi−zvj0⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪=δi

其中 Tvi=vi+d , δi 是初始网格在点 vi 处的拉普拉斯坐标。
(3)对旋转变换铭感

∑j∈N(i)wij(Rvi−Rvj)=R∑j∈N(i)wij(vi−vj)=Rδi

其中 R是旋转变换， δi 是初始点的拉普拉斯坐标。
下面介绍微分坐标变换的整体形式。
Δ=L(V)
在这里由于L是非奇异的为了求解这个方程组需要增加一些固定的点
v′i=ui
这样整个公式的求解可以变换为

V˜′=argv′min(||L(V′)−Δ||2+∑i∈C||v′i−ui||)

拉普拉斯网格变形的本质是通过求解线性方程组.通过上式可求得各个网格顶点的三维坐标.
这样通过求解方程组得到新的坐标以后就可以重构出新的三维模型。
由于拉普拉斯坐标对旋转的敏感性。这样在进行后续进行旋转操作时容易发生变形。当然后续论文中回提出解决这个问题的方法。这里就不细说了。

参考文献：
1、《Differential Coordinates for Interactive Mesh Editing》
2、《基于微分坐标的网格morphing》
3 《Laplacian Surface Editing》
4 《拉普拉斯坐标在网格变形中的应用研究》