Leetcode由浅入深（二），炒股票系列

在Leetcode中，有这么一类基于某些场景的问题，虽然归根到底也是算法，但是却给枯燥的算法带来了些许的活力。那么，我们就来看一下，Leetcode中最经典的实际应用题——炒股票

一、Best Time to Buy and Sell Stock

题目的大意是你是个股民，然后你还有预知未来的能力，于是你通过这个能力得知了之后每天股票的价格，你可以从任意一天买入股票，也可以在任意一天卖掉，但是你只能进行一次交易。作为炒股人，当然是要把利润最大化。这个问题转化为算法问题就是找到一个数组中前后增值最大的两个数，并返回差值。

第一种想法是每当遇到比当前出现还要低的数的时候就重新设定最低值，然后遍历数组找到最大差值。

Java代码如下

public int maxProfit(int[] prices) {
        if (prices.length == 0) {
			 return 0 ;
		}
        int min = prices[0];
        int max = 0;
        for(int i = 0; i < prices.length; i ++) {
            if(prices[i] > min) {
                max = Math.max(max, prices[i] - min);
            }else{
                min = prices[i];
            }
        }
        return max;
    }

另一种算法的基本逻辑是计算差值，找到能提供最大利润的连续子数组，每当赔了，就从0开始。

Java代码如下

public int maxProfit(int[] prices) {
        int maxCur = 0, maxSoFar = 0;
        for(int i = 1; i < prices.length; i++) {
            maxCur = Math.max(0, maxCur += prices[i] - prices[i-1]);
            maxSoFar = Math.max(maxCur, maxSoFar);
        }
        return maxSoFar;
    }

二、无限购买权

问题二情景与问题一大致相同，不过你可以购买任意次股票。

这个问题初看感觉仿佛很有深意，然后仔细想一下就会发现这个问题就是考察你是否能把实际模型转化为算法问题。

仔细想想就会发现只要今日的股票比前一天值钱，那我就买入股票，如果不值钱，那我就不买股票。答案也就变得相当直观了。

public int maxProfit(int[] prices) {
        int total = 0;
        for (int i=0; i< prices.length-1; i++) {
            if (prices[i+1]>prices[i]) total += prices[i+1]-prices[i];
        }
        return total;
    }

三、两次交易

经过上次你疯狂购买后，股票市场被你扰乱了，于是他们规定，在接下来的时间内，没人只能购买并出售最多两次股票，并且你持有股票时不能再次买入（即你不能同时持有两份股票）。

这个问题的解法为，你可以先购买一次股票，并在恰当时机卖掉，然后再购买一次股票，再卖掉。

假定开始时你身无分文。 那么我们第一次买入时（第i天）相当于欠了市场prices[i]的钱。当你卖掉第一次买入的股票时（第j天），你相当于赚了price[j]-prices[i]的钱。然后你在下一次购买前，你就获得了价值为price[j]-prices[i]的本金。那么你第二次购买时开局的起始金钱将不再是0. 你将在这个基础上重复第一次的行为，来赚取最多的钱。 当我们保持遍历，我们会获得两次交易限制下的最高额度（不一定必须交易两次，也许第一次交易一直在挣钱，所以你没有必要买入第二次。你可以将第二次买入想象成第一次卖掉后立刻再买入）

Java代码如下

public int maxProfit(int[] prices) {
        //开始购买时身无分文，所以相当于在欠债。
        int buy1 = Integer.MIN_VALUE, buy2 = Integer.MIN_VALUE, sell1 = 0, sell2 = 0;
       for(int price: prices){
         //到目前为止第一次交易购买时我们手中的资产
         buy1 = Math.max(buy1, -price);
         //到目前为止第一次交易出售时我们手中的资产
         sell1 = Math.max(sell1, price + buy1);
         //到目前为止第二次交易购买时我们手中的资产
         buy2 = Math.max(buy2, sell1 - price);
         //到目前为止第二次交易出售时我们手中的资产
         sell2 = Math.max(sell2, price + buy2);
       }
       return sell2;
    }

通过这道题，我们可以发现，虽然我们要回归算法，但是有时代入情景，然而更好理解。

四、K次交易

经过调控，市场回归了稳定，于是官方渐渐开放了购买的次数，于是你可以进行K次交易。
这个问题可以用动态规划的方法来解决。逻辑其实等同于之前的2此交易逻辑。

class Solution {
    public int maxProfit(int k, int[] prices) {
        if(k < 1) return 0;
        if(prices == null || prices.length <= 1) return 0;
        //corner case: 当K大于日子的一半的时候，我们可以保证能够在有利润时都买入
        int len = prices.length;
        if(k >= len/2) {
            int profit = 0;
            for(int i = 1; i < len; i ++) {
                if(prices[i] > prices[i - 1]) {
                    profit += prices[i] - prices[i - 1];
                }
            }
            return profit;
        }
        //K次交易动态规划t(i, j)代表用i次交易在第j天的最大收入
        int[][] t = new int[k + 1][len];
        for (int i = 1; i <= k; i++) {
            //假定开始买入了
            int tmpMax =  -prices[0];
            for (int j = 1; j < len; j++) {
                //比较当天卖出或者不卖之间的大者
                t[i][j] = Math.max(t[i][j - 1], prices[j] + tmpMax);
                //比较当天买入或者不买之间的大者
                tmpMax =  Math.max(tmpMax, t[i - 1][j - 1] - prices[j]);
            }
        }
        return t[k][len - 1];

    }
}

这种方法要消耗较多的空间，我们可以将二维降至一维数组。
Java代码如下

public int maxProfit(int k, int[] prices) {
        if(k < 1) return 0;
        if(prices == null || prices.length <= 1) return 0;
        //corner case: 当K大于日子的一半的时候，我们可以保证能够在有利润时都买入
        if(k >= prices.length/2) {
            int profit = 0;
            for(int i = 1; i < prices.length; i ++) {
                if(prices[i] > prices[i - 1]) {
                    profit += prices[i] - prices[i - 1];
                }
            }
            return profit;
        }
        //K次交易动态规划
        int[] buy = new int[k + 1];
        int[] sale = new int[k + 1];
        for(int i = 0; i <= k; i ++) {
            buy[i] = Integer.MIN_VALUE;
            sale[i] = 0;
        }
        for (int i = 0; i < prices.length; i++){
            for (int j = k; j > 0; j--){
                sale[j] = Math.max(sale[j], prices[i] + buy[j]);
                buy[j] = Math.max(buy[j], sale[j-1] - prices[i]);
            }
        }
        
        return sale[k];

    }

五、交易费

经过一段时间的运营，股票市场良好，官方决定解除交易次数限制，并通过收取交易费用来调控过多买入。

我们这里仍然采用与之前相同的情景分析来理解，我们可以理解为这样： 对于一只股票，我们在某一天可以持有，也可以不持有。从这点切入，我们只要找到在最后一天不持有股票时收益最高的情况就可以了。

Java代码如下：

public int maxProfit(int[] prices, int fee) {
        int l = prices.length;
        int[] hold = new int[l + 1]; //Hold the stock until day i;
        int[] unhold = new int[l + 1]; //Do not hold the stock until day i;
        hold[0] = Integer.MIN_VALUE;
        for(int i = 1; i <= prices.length; i ++) {
            hold[i] = Math.max(hold[i - 1], unhold[i - 1] - prices[i - 1] - fee);
            unhold[i] = Math.max(unhold[i - 1], hold[i - 1] + prices[i - 1]);
        }
        return unhold[l];
    }

六、购买间隔

收取交易费试运营后效果并不好，于是官方想到了新方法来调控股票市场，他们要求用户在卖出自己的股票后必须隔一天才能再次购买。分析流程图如下。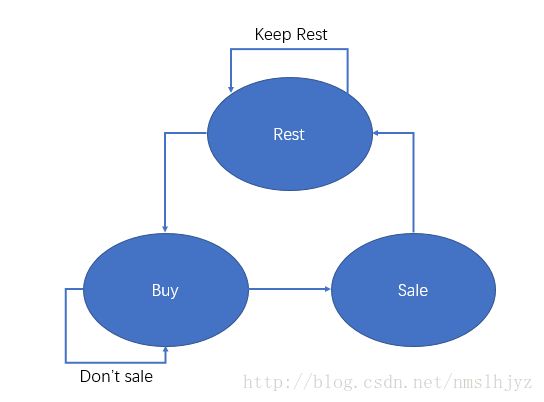

public int maxProfit(int[] prices) {
        if(prices == null || prices.length <= 1) return 0;
        int len = prices.length;
        int rest[] = new int[len];
        int buy[] = new int[len];
        int sale[] = new int[len];
        buy[0] = -prices[0];
        rest[0] = 0;
        sale[0] = 0;
        for(int i = 1; i < len; i ++) {
            rest[i] = Math.max(rest[i - 1], sale[i - 1]);
            buy[i] = Math.max(rest[i - 1] - prices[i], buy[i - 1]);
            sale[i] = buy[i - 1] + prices[i];
        }
        return Math.max(rest[len - 1], sale[len - 1]);
    }

到此为止，你炒股大获成功，你也成为炒股界一名闪耀的新星。希望大家看了这个故事，能够对炒股票这类问题有所收获。