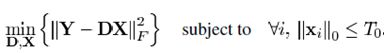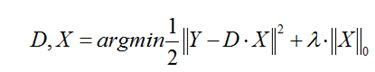K-SVD字典学习详细推导

                                         K-SVD字典学习

  最近学习K-SVD字典学习算法，云里雾里地看了好几篇博客，最后老实阅读了算法的原始论文《K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation》和维基百科的讲解，不得不说还是外国人描述细致，推导认真严谨。

一、K-SVD算法

1、预备知识

  稀疏编码算法是一种无监督学习方法，它用来寻找一组“超完备”基向量来更高效地表示样本数据。稀疏编码算法的目的就是找到一组基向量 ，使得我们能将输入向量表示为这些基向量的线性组合。

2、K-SVD字典学习建模（模型和策略）

  K-SVD字典学习就是一种稀疏编码过程，该算法基于样本集要寻找的一组“超完备”基向量叫做字典矩阵D，基向量的便是字典D的列向量；样本集中任意样本可以根据字典求得其对应的稀疏表示。字典学习其实可以看成是一种矩阵分解形式地学习，对于样本集Y,

                                                                                            

  M为样本数，单个样本(或者单条信号),是一个N维特征向量，单个样本组成样本集总体矩阵Y,矩阵的每一列为一个样本。字典矩阵D表示为，成之为原子向量，原子向量维度也为N，K个原子向量按列排列组成字典矩阵D，

                                                                             

字典学习一般学习的是超完备字典（Overcomplete Dictionaries）。字典学习的目标是学习一个字典矩阵D，使得Y被近似分解为

                                                                                           

 同时满足，D的每一列为单位化原子向量，X尽可能稀疏。目标函数的数学表达式论文中给出两种表达形式：

（1）表达形式一：

                                                         

 学习字典D使得重构误差尽可能小， 0范数表示系数向量非零项的数量，为稀疏度约束阈值，是一个常数，即约束非零项数目。

（2）表达形式二：

                                                        

 ε是重构误差所允许的最大值。其他博客有第三种方式，因为这个是一个带约束的优化目标函数，因此可以采用拉格朗日乘子法分解为：

                                                      

  这种形式因为L0难以求解，所以实际上一般用L1正则项替代近似。同其他机器学习建模一样，数学模型为求解样本矩阵的矩阵分解，策略（优化目标如上所述）。

3、K-SVD算法

  有了模型和策略，就需要知道求解满足优化目标的算法，即学习算法。K-SVD的优化策略为最小化如下目标函数：

                                                          

  如果直接限制,则问题本质上就是我们熟悉的k-means聚类（k-means的类别标签如果采用one-hot编码，其实就是样本集稀疏编码，只是此时稀疏编码仅仅允许一个非零项，而字典D每一列就是其聚类中心，D的更新采用的是各自类的样本求均值更新），而原论文提到K-SVD字典学习是k-means的推广，并放松了对系数矩阵X的约束,即系数矩阵可放松，即有。

算法的流程主要分为三大步，论文描述也非常清晰：

                                             

维度信息：，算法求解思路主要为交替迭代的进行稀疏编码和字典更新。

 （1）随机选取样本集Y中的K个样本初始化字典D，D中每一列为一个样本特征向量，并对特征想做了L2归一化处理，

                                                                                    

系数编码矩阵所有稀疏初始化为0.

 （2）稀疏编码阶段

  该阶段固定字典D,求解样本集中所有样本的稀疏编码。对于样本集中每一个样本及其对应稀疏编码,有：

                                              

或者

                                           

维基百科：In the K-SVD algorithm, the D  is first fixed and the best coefficient matrix X is found. As finding the truly optimal X is impossible, we use an approximation pursuit method. Any algorithm such as OMP, the orthogonal matching pursuit can be used for the calculation of the coefficients, as long as it can supply a solution with a fixed and predetermined number of nonzero entries .

  以此为目标或者说是约束求解稀疏编码，这个带约束的优化目标函数很难求解得到最优的系数矩阵X,采用OMP（the orthogonal matching pursuit）算法,该算法可以满足对稀疏度的约束条件（这个在python的sklearn库中有对应函数，可以直接调用）。求得所有样本稀疏编码以后，在重构误差函数，如果满足约束条件则不在更新字典，如果不满足则进入下一步更新字典。

（3）更新字典D及系数矩阵X的非零项。

  此时固定字典D和稀疏矩阵X,对于字典矩阵D中的每一列原子向量进行更新并同时更新对应行的X。因为要更新第k个原子向量，此时优化的目标函数可以写成：

                                                              

将第k列原子分解出来，同时对应的稀疏矩阵第k行分解出来，整个目标函数分解为

                                                                                       

  论文提到如果直接对做SVD分解则会使得零项被填充，亦即稀疏性被破坏。因此仅仅选择的非零项所对应的样本id（非零项对应列且与对应的）参与计算，定义非零项集合，设非零集合元素个数为B：

                                                                      

  定义矩阵,矩阵的维度为(N,B)，在出索引的元素置1，其余位置为0，左乘有  ,此时仅仅是非零项的组合。同理有,的维度为（M,B）,该矩阵的列所对应的样本与的非零项对应，且用到原子。基于此目标函数左乘变为：

                                                                    

此时便不会影响的稀疏度，仅仅对非零项相关的样本进行计算。

  此时对矩阵进行SVD分解更新原子和，的分解如下：

                                                                      

  则求解的就是U矩阵的第一列，系数矩阵为V矩阵的第一列乘上。按照这种解法实际上U矩阵列已经是归一化的，所以直接可以作为最终结果。

  对字典D进行上述计算，更新所有原子和中所有非零项以后，还需要判断是否学习是否收敛否则重复步骤（2）和（3）直至收敛。那么收敛条件呢？可以通过进入步骤（2），固定更新的D，求系数矩阵X，然后重构误差损失

                                                                                 

 

  若重构误差小于ε则收敛，停止迭代，若不满足继续执行更新字典的步骤（3），如此循环往复直至收敛；也可以通过判断当前更新后的字典原子与更新前原子的均方误差（MSE），若MSE逐渐变小并最后区域稳定则收敛。

二、K-SVD的python简单实现

#coding=utf-8
import numpy as np
from sklearn import linear_model
from sklearn.preprocessing import normalize
import scipy.misc
from matplotlib import pyplot as plt
import random


class KSVD(object):
    def __init__(self, k, max_iter=30, tol=1e-6,
                 n_nonzero_coefs=None):
        """
        稀疏模型Y = DX，Y为样本矩阵，使用KSVD动态更新字典矩阵D和稀疏矩阵X
        :param n_components: 字典所含原子个数（字典的列数）
        :param max_iter: 最大迭代次数
        :param tol: 稀疏表示结果的容差
        :param n_nonzero_coefs: 稀疏度
        """
        self.dictionary = None
        self.sparsecodeX = None
        self.max_iter = max_iter
        self.sigma = tol
        self.k_components =k
        self.n_nonzero_coefs = n_nonzero_coefs

    def _initialize(self, y):

        # u, s, v = np.linalg.svd(y)
        # self.dictionary = u[:, :self.k_components]
        """
        随机选取样本集y中n_components个样本,并做L2归一化
        #  """
        ids=np.arange(y.shape[1])                                     #获得列索引数组
        select_ids=random.sample(ids, self.k_components ) #随机选取k_components个样本的id,k-svd之K
        mid_dic=y[:,np.array(select_ids)]                           #数组切片提取出k个样本
        self.dictionary=normalize(mid_dic, axis=0, norm='l2')  #每一列做L2归一化

        print self.dictionary.shape

    def _update_dict(self, y, d, x):
        """
        使用KSVD更新字典的过程
        """
        for i in range(self.k_components):
            index = np.nonzero(x[i, :])[0]  #非零项索引数组
            if len(index) == 0:
                continue

            d[:, i] = 0
            r = (y - np.dot(d, x))[:, index]                      #获取非零项对用id的列
            u, s, v = np.linalg.svd(r, full_matrices=False)  #SVD分解
            d[:, i] = u[:, 0]
            x[i, index] = s[0] * v[0, :]
        return d, x

    def fit(self, y):
        """
        KSVD迭代过程
        """
        self._initialize(y)
        for i in range(self.max_iter):
            x = linear_model.orthogonal_mp(self.dictionary, y, n_nonzero_coefs=self.n_nonzero_coefs)
            e = np.linalg.norm(y - np.dot(self.dictionary, x))
            print i, e
            if e < self.sigma:
                break
            self._update_dict(y, self.dictionary, x)


        self.sparsecodeX = linear_model.orthogonal_mp(self.dictionary, y, n_nonzero_coefs=self.n_nonzero_coefs)
        return self.dictionary, self.sparsecodeX


if __name__ == '__main__':

    im_ascent = scipy.misc.ascent().astype(np.float)
    ksvd = KSVD(300,100,0.00005,200)
    dictionary, sparsecode = ksvd.fit(im_ascent)
    plt.figure()
    plt.subplot(1, 2, 1)
    plt.imshow(im_ascent)
    plt.subplot(1, 2, 2)
    plt.imshow(dictionary.dot(sparsecode))
    plt.show()

 

另一个github实现（图像去噪）：

https://github.com/alsoltani/K-SVD

参考文献：

[1] Aharon M, Elad M, Bruckstein A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on signal processing, 2006, 54(11): 4311.

[2] 维基百科：https://en.wikipedia.org/wiki/K-SVD

[3] 博客：https://blog.csdn.net/theonegis/article/details/78453909

[4] 博客：https://blog.csdn.net/hjimce/article/details/50810129