数据结构:zyf树/毒瘤树
upd:把它叫成宗法树被lxl骂了,现在改一下
ps:由于CSDN没有替换功能,而且博主很懒,所以下面名字不改,大家清楚就好(逃
一看题目是不是很懵逼?
那就对了!
这个数据结构本来是没有名字的,由一个毒瘤dalao发明并传给讲师,讲师再交给我们。
至于这个名字,则是学员中一位毒瘤想到的。原因待会儿再讲。
为了方便,以下就称这种数据结构为“宗法树”。
宗法树是一种类似于平衡树的数据结构,但似乎更简单。它支持以下6种功能:
1、插入x
2、删除x(若有多个x,只删除一个)
3、求x的排名(严格比x小的数的个数+1)
4、求第x个数(同上)
5、求x的前驱(最大的小于x的数)
6、求x的后继(最小的大于x的数)
以上6种功能均为平衡树基本功能,但用代码量更小的宗法树也可以实现。
宗法树的性质:
1、是一棵二叉树
2、它的数字都存在叶子节点里
3、非叶子节点存储子树的最大值/最小值
4、每个非叶子节点的左子树里的数全都小于右子树里的数。
5、每个非叶子节点都必须有两棵子树
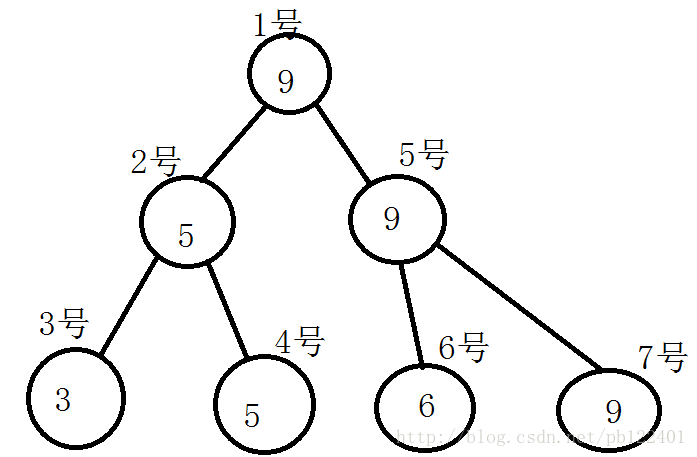
比如这样一棵宗法树:
而下面,我将按顺序讲解每一种功能的实现。
1、插入
以上面那棵宗法树为例,如果我们想插入6:
1、从根节点出发,发现左儿子的值是5<6,于是向右儿子递归
2、发现5号节点是叶子节点,于是在5号节点下方再建两个新节点6、7
3、5号节点原来的值9>6,所以将9放到右儿子,6放到左儿子
4、回溯更新
插入结果:
代码实现:
void insert(int &k,int x)
{
if (!k)//没有这个点,即第一次插入
{
new_tr(k,x);//动态开点
return;
}
if (leaf(k))//叶子节点
{
new_tr(tr[k].lson,min(x,tr[k].v));//建左儿子
new_tr(tr[k].rson,max(x,tr[k].v));//建右儿子
push_up(k);//更新当前节点
return;
}
int l=tr[tr[k].lson].v;//左子树最大值
if (x>l) insert(tr[k].rson,x);//大于左子树最大值,向右递归
else insert(tr[k].lson,x);//向左递归
push_up(k);//更新当前节点
}2、删除节点
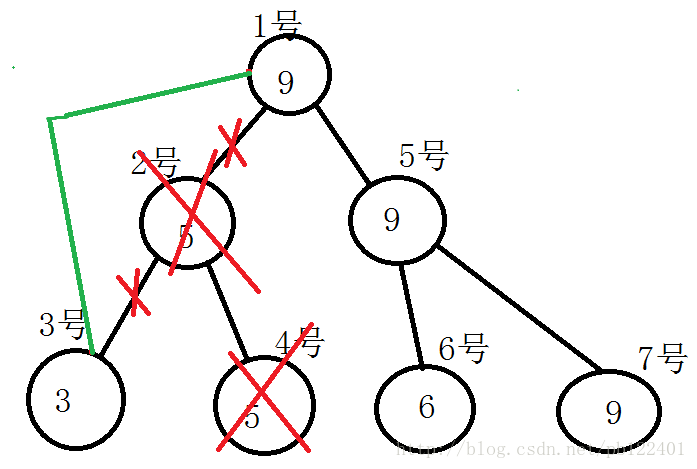
从上一次插入结果开始,以删除5为例:
1、从根节点开始,左儿子2号节点的值5>=5,向左递归
2、2号节点的左儿子的值3<=5,向右递归
3、找到5,将4号节点删除
4、删除后2号节点只有左儿子,没有右儿子,因此该节点没有意义,用3号节点将其代替
5、将删除的节点回收(可以没有)
6、回溯更新
删除结果:
代码实现(不带回收功能):
void del(int k,int fa,int x)//fa是k的父节点
{
if (leaf(k))//叶子节点
{
if (tr[k].v==x)//找到x
{
if (tr[fa].lson==k) tr[fa]=tr[tr[fa].rson];//x是左儿子,用右儿子代替父节点
else tr[fa]=tr[tr[fa].lson];//x是右儿子,用左儿子代替父节点
}
return;
}
int l=tr[tr[k].lson].v;//左子树最大值
if (x>l) del(tr[k].rson,k,x);//大于左子树最大值,向右递归
else del(tr[k].lson,k,x);//向左递归
push_up(k);//更新当前节点
}3、求x的排名
这个更容易实现,每次:
1、叶节点,值不比x小,返回1
2、叶节点,值比x小,返回2
2、x比左儿子值大,返回向右递归结果+左子树size
3、x不比左儿子值大,返回向左递归结果
代码实现:
int rnk(int k,int x)
{
if (leaf(k))//叶节点
{
if (x>tr[k].v) return 2;//第二种
return 1;//第一种
}
int l=tr[tr[k].lson].v;//左子树最大值
if (x>l) return rnk(tr[k].rson,x)+tr[tr[k].lson].sz;//第三种
return rnk(tr[k].lson,x);//第四种
}4、求排名为x的数
也很容易。分三种可能:
1、叶节点,返回节点值
2、左子树size<=x,结果在左子树内,向左递归x
3、左子树size>x,结果在右子树内,向右递归(x-左子树size)
代码实现:
int kth(int k,int rnk)
{
if (leaf(k)) return tr[k].v;//第一种
if (rnk<=tr[tr[k].lson].sz) return kth(tr[k].lson,rnk);//第二种
return kth(tr[k].rson,rnk-tr[tr[k].lson].sz);//第三种
}5、求x的前驱
根据第3第4种功能,可以得出x前驱=kth(root,rnk(root,x)-1)
6、求x的后继
同样根据第3第4种功能,得出x后继=kth(root,rnk(root,x+1))
附加优化:
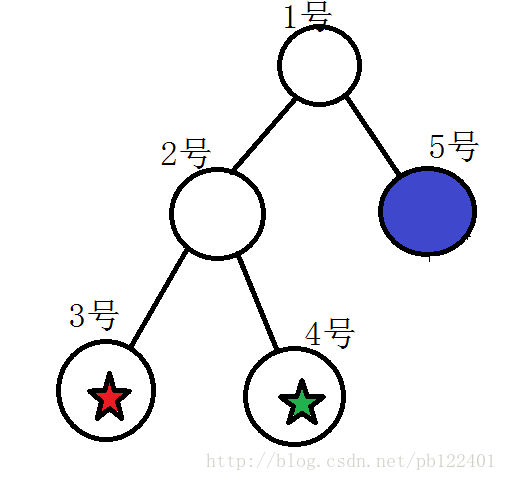
由于加点删点的方法,可能会出现有一棵子树深度特别大,而另一边特别小的状况,导致递归时间过长,如下图:
其中五角星代表下面还有深度巨大的子树,颜色只是为了区分
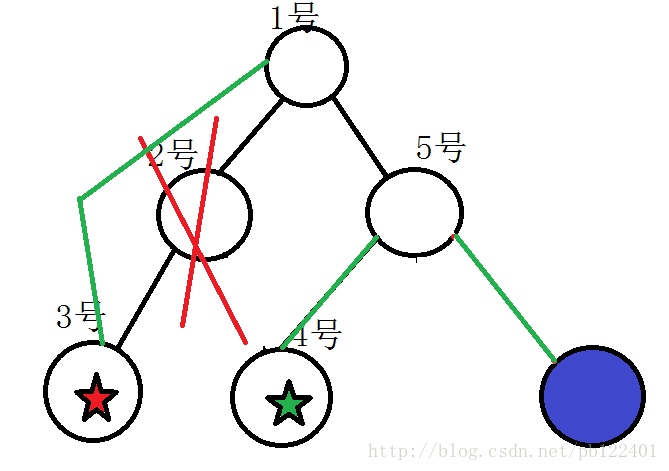
对此,可以将一棵子树上的一些信息转移到另一棵子树上去,而同样保证性质没有被破坏,如上图可以被转化为下图的状态:
其中绿色边是新增边
代码实现如下:
void rotate(int k,bool dir)//自行理解
{
if (!dir)
{
int r=tr[k].rson;
tr[k].rson=tr[k].lson;
tr[k].lson=tr[tr[k].rson].lson;
tr[tr[k].rson].lson=tr[tr[k].rson].rson;
tr[tr[k].rson].rson=r;
push_up(tr[k].lson);
push_up(tr[k].rson);
}
else
{
int l=tr[k].lson;
tr[k].lson=tr[k].rson;
tr[k].rson=tr[tr[k].lson].rson;
tr[tr[k].lson].rson=tr[tr[k].lson].lson;
tr[tr[k].lson].lson=l;
push_up(tr[k].lson);
push_up(tr[k].rson);
}
}
void maintain(int k)
{
if (leaf(k)) return;//是叶子节点,不用修改
if (tr[tr[k].lson].sz>=tr[tr[k].rson].sz*4) rotate(k,0);//左儿子太重
if (tr[tr[k].rson].sz>=tr[tr[k].lson].sz*4) rotate(k,1);//右儿子太重
}
例题:洛谷 P3369 模板平衡树
链接:https://www.luogu.org/problemnew/show/P3369
AC代码:
#include
using namespace std;
struct hh
{
int v,sz,lson,rson;
}tr[1010101];
int cnt,n,root;
bool leaf(int x){return !(tr[x].lson||tr[x].rson);}
void new_tr(int &k,int x)
{
k=++cnt;
tr[k].v=x;
tr[k].sz=1;
}
void push_up(int x)
{
if (leaf(x)) return;
tr[x].v=max(tr[tr[x].lson].v,tr[tr[x].rson].v);
tr[x].sz=tr[tr[x].lson].sz+tr[tr[x].rson].sz;
}
void rotate(int k,bool dir)//自行理解
{
if (!dir)
{
int r=tr[k].rson;
tr[k].rson=tr[k].lson;
tr[k].lson=tr[tr[k].rson].lson;
tr[tr[k].rson].lson=tr[tr[k].rson].rson;
tr[tr[k].rson].rson=r;
push_up(tr[k].lson);
push_up(tr[k].rson);
}
else
{
int l=tr[k].lson;
tr[k].lson=tr[k].rson;
tr[k].rson=tr[tr[k].lson].rson;
tr[tr[k].lson].rson=tr[tr[k].lson].lson;
tr[tr[k].lson].lson=l;
push_up(tr[k].lson);
push_up(tr[k].rson);
}
}
void maintain(int k)
{
if (leaf(k)) return;//是叶子节点,不用修改
if (tr[tr[k].lson].sz>=tr[tr[k].rson].sz*4) rotate(k,0);//左儿子太重
if (tr[tr[k].rson].sz>=tr[tr[k].lson].sz*4) rotate(k,1);//右儿子太重
}
void insert(int &k,int x)
{
if (!k)//没有这个点,即第一次插入
{
new_tr(k,x);//动态开点
return;
}
if (leaf(k))//叶子节点
{
new_tr(tr[k].lson,min(x,tr[k].v));//建左儿子
new_tr(tr[k].rson,max(x,tr[k].v));//建右儿子
push_up(k);//更新当前节点
return;
}
int l=tr[tr[k].lson].v;//左子树最大值
if (x>l) insert(tr[k].rson,x);//大于左子树最大值,向右递归
else insert(tr[k].lson,x);//向左递归
push_up(k);//更新当前节点
}
void del(int k,int fa,int x)//fa是k的父节点
{
if (leaf(k))//叶子节点
{
if (tr[k].v==x)//找到x
{
if (tr[fa].lson==k) tr[fa]=tr[tr[fa].rson];//x是左儿子,用右儿子代替父节点
else tr[fa]=tr[tr[fa].lson];//x是右儿子,用左儿子代替父节点
}
return;
}
int l=tr[tr[k].lson].v;//左子树最大值
if (x>l) del(tr[k].rson,k,x);//大于左子树最大值,向右递归
else del(tr[k].lson,k,x);//向左递归
push_up(k);//更新当前节点
}
int rnk(int k,int x)
{
if (leaf(k))//叶节点
{
if (x>tr[k].v) return 2;//第二种
return 1;//第一种
}
int l=tr[tr[k].lson].v;//左子树最大值
if (x>l) return rnk(tr[k].rson,x)+tr[tr[k].lson].sz;//第三种
return rnk(tr[k].lson,x);//第四种
}
int kth(int k,int rnk)
{
if (leaf(k)) return tr[k].v;//第一种
if (rnk<=tr[tr[k].lson].sz) return kth(tr[k].lson,rnk);//第二种
return kth(tr[k].rson,rnk-tr[tr[k].lson].sz);//第三种
}
int main()
{
scanf("%d",&n);
for (int i=1;i<=n;i++)
{
int opt,x;
scanf("%d %d",&opt,&x);
if (opt==1) insert(root,x);
if (opt==2) del(root,0,x);
if (opt==3) printf("%d\n",rnk(root,x));
if (opt==4) printf("%d\n",kth(root,x));
if (opt==5) printf("%d\n",kth(root,rnk(root,x)-1));
if (opt==6) printf("%d\n",kth(root,rnk(root,x+1)));
}
} //由于其删除时父死兄继和旋转时很像过继的特点,称其为宗法树。
upd:由于被lxl骂了,将该句注释掉(逃