VLocNet++: Deep Multitask Learning for Semantic Visual Localization and Odometry 辅助学习 && 2018 论文笔记

---

作者：Noha Radwan∗Abhinav Valada∗Wolfram Burgard

研究机构：德国弗莱堡大学

论文解决的问题

本文解决了语义分割+相机重定位+视觉里程计VO三个任务。相机重定位指的是绝对位姿预测，VO则是相对位姿预测。本文还发布了一个用于定位的数据集DEEPLOC dataset.

多任务学习模型的好处是可以提高模型的泛化性，不需要大量的标签数据，且一次计算完成了多个任务，效率高。

本文基于VLocNet，提出了一种自适应的加权方法，能够利用运动特定时间信息（motion-specific temporalinformation）来提高定位精度。这种自适应加权方法，在融合网络的两个特征图时，可以调整加权权值得到更加合适的权值比例，得到的融合入特征图能够更好的描述特征信息。

本文在VLocNet的基础上加以改进：

1. 联合前一帧的信息来对运动特定信息（motion specific information）进行累积
2. 使用提出的自适应融合层对激活区域的语义特征进行自适应融合
3. 提出一种自监督变换层（warping），在语义分段模型中聚合场景级上下文。

论文方法介绍

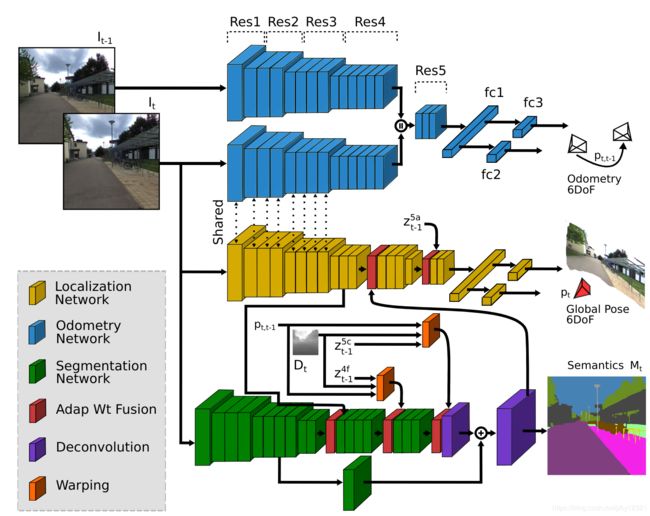
模型结构：相对位回归网络（VO模块）、绝对位姿回归网络、语义分割网络

绝对位姿回归网络：

上图中间黄色的部分。中间两层红色的是本文提出的自适应权重融合层。

损失函数：
$$L_{loc}(f(\theta |I_t)):=L_{Euc}(f(\theta |I_t))+L_{Rel}(f(\theta |I_t))$$
其中几何一致损失（相对位姿损失）：
$$\begin{gathered} L_{Rel}(f(\theta |I_t))=L_{x_{Rel}}(f(\theta |I_t))exp(-{\hat{s}}_{x_{Rel}})+{\hat{s}}_{x_{Rel}}+L_{q_{Rel}}(f(\theta |I_t))exp(-{\hat{s}}_{q_{Rel}})+{\hat{s}}_{q_{Rel}} \\ 平移损失：L_{x_{Rel}}(f(\theta |I_t)):=\Vert x_{t,t-1}-({\hat{x}}_t-{\hat{x}}_{t-1}){\Vert }^2 \\ 旋转损失：L_{q_{Rel}}(f(\theta |I_t)):=||q_{t,t-1}-({\hat{q}}_{t-1}^{-1}{\hat{q}}_t)|{|}^2 \end{gathered}$$

欧氏距离损失（绝对位姿损失）：
$$\begin{gathered} L_{Euc}(f(\theta |I_t))=L_x(f(\theta |I_t))exp(-{\hat{s}}_x)+{\hat{s}}_x+L_q(f(\theta |I_t))exp(-{\hat{s}}_q)+{\hat{s}}_q \\ 平移损失：L_x(f(\theta |I_t)):=\Vert x_t-{\hat{x}}_t{\Vert }^2 \\ 旋转损失：L_q(f(\theta |I_t)):=\Vert q_t-{\hat{q}}_t{\Vert }^2 \end{gathered}$$

VO模块:

上图中蓝色的两支。

注意下面的一支与 绝对位姿回归网络由于都在$I_t$上提特征，所以是共享权重的。

损失函数：
$$\begin{gathered} L_{vo}(f(\theta |I_t,I_{t-1})):=L_x(f(\theta |I_t,I_{t-1}))exp(-{\hat{s}}_{x_{vo}})+{\hat{s}}_{x_{vo}}+L_q(f(\theta |I_t,I_{t-1}))exp(-{\hat{s}}_{q_{vo}})+{\hat{s}}_{q_{vo}} \\ {L}_x、L_q分别表示平移损失和旋转损失 \end{gathered}$$

语义分割模块：

上图中绿色的部分。

首先计算每个像素的类别：
$$\begin{gathered} p_j(u_r,\theta |I_n)=\frac{exp(s_j(u_r,\theta ))}{{\sum }_k^{C}exp(s_k(u_r,\theta ))} \\ {s}_j(u_r,\theta )代表像素u_r的得分，\theta 为模型权重 \end{gathered}$$
损失函数:
$$\begin{gathered} L_{seg}(T,\theta )=-\sum _{n=1}^N\sum _{r=1}^{\rho }\sum _{j=1}^C{\delta }_{m_r^n,j}log{p}_j(u_r,\theta |I_n) \\ C:classnumber \\ N:imagesnumber \\ \rho :pixelnumberperimage \end{gathered}$$
然后介绍自监督的变换层：

self-supervised Warping:

上图中橘色的网络层

根据t-1时刻的特征图生成对应的深度图（用DispNet），然后利用估计的相对位姿将其变换到t时刻的视角下，将其与特时刻的特征图融合。这样多视角、多分辨率的信息使得模型对视角、尺度、畸变等场景下依然有很强的鲁棒性。

数学表达 ：
$$\begin{gathered} u_r:=\pi (T(p_{t,t-1}){\pi }^{-1}(u_r,D_t(u_r))) \\ {D}_t表示深度图 \\ T(p_{t,t-1})表示相对位姿p_{t,t-1}对应的齐次旋转矩阵 \\ \pi 表示投影函数 \end{gathered}$$

adaptive weighted fusion layer：

用于组合来自多个层或多个网络的特征的常用做法是：执行张量的级联或逐元素的加法/乘法。 尽管这在两个张量都包含足够的相关信息时可能是有效的，但这种操作通常会累积不相关的特征图，它的有效性在很大程度上取决于进行融合的网络的中间层。

这里作者提出了可以自适应加权的机制：

假设两张特征图为$z^a{z}^b$,则自适应融合女机制可写为：
$$\begin{gathered} {\hat{z}}_{fuse}=max(W\ast ((w^a\odot z^a)\oplus (w^b\odot z^b))+b,0) \\ W、b:非线性池化的参数(即1\ast 1卷基层+ReLU) \\ \odot :对应通道相乘 \\ \oplus :对应通道相连接 \\ \ast :卷积操作 \end{gathered}$$

总的损失函数：

$$L_{multi}:=L_{loc}exp(-{\hat{s}}_{loc})+{\hat{s}}_{loc}+L_{vo}exp(-{\hat{s}}_{vo})+{\hat{s}}_{vo}+L_{seg}exp(-{\hat{s}}_{seg})+{\hat{s}}_{seg}$$

其中$\hat{s}$均指可学习的权值参数。

实验内容以及分析

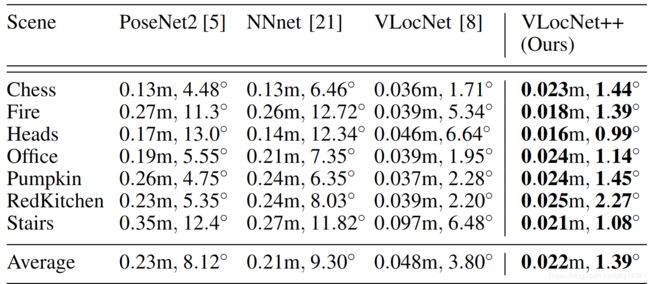
7-SCENES数据集，定位对比：

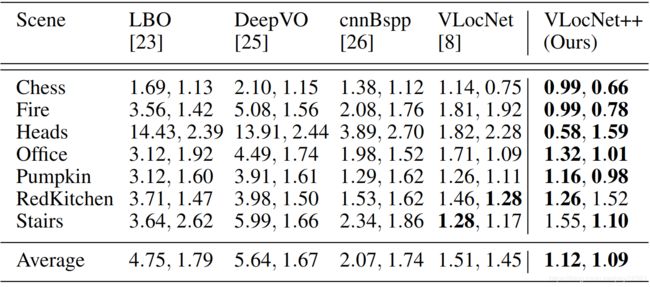
7-SCENES数据集，VO对比：

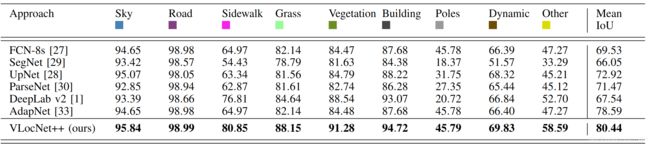
DEEPLOC DATASET，语义分割对比：

VO性能可视化：

在户外、户内、重复文理、无文理、反射等环境下都有较好的鲁棒性