Geometric loss functions for camera pose regression with deep learning

深度学习定位系列2_PoseNet改进

论文：Geometric loss functions for camera pose regression with deep learning

1 摘要

  深度学习在单目图像重定位任务上表现出了高鲁棒性和实时性。PoseNet模型利用深度CNN学习单张图像的6DO（6自由度）F相机位姿。PoseNet使用高层特征进行定位，在基于SIFT的定位方法失效的情形（如：光照变化、运动模糊、未知相机内参），具有较好的鲁棒性。但PoseNet所设计的损失函数采用L2距离，造成超参数的训练难度较大。针对PoseNet损失函数设计具有缺陷的问题，本文所介绍的这篇文章基于几何以及重投影误差构造损失函数；除此以外，该文章提出了一种自动学习最优平衡权重（指损失函数中位置损失与姿态损失的权重因子）的方法。实验证明，无论在室内还是室外城市场景，该文章所提出的方法均优于PoseNet。

2 实验结果

2.1 数据集简介

  除了PoseNet使用的室内数据Cambridge Landmarks以及室外数据7scenes，还采用了Dubrovnik 6K。

2.2 实验分析

2.2.1 损失函数性能对比

  实验部分首先对损失函数对定位估计性能的影响进行分析，实验结果如下：

  由实验结果，本篇论文建议模型采用2步训练方法：先使用文献[3]中的损失函数进行训练；然后使用重投影损失对模型进行微调。

2.2.2 定位精度基线评测

  作者在7Scenes和Cambridge Landmarks对所提出方法进行试验评测，试验结果如下图所示。从实验结果可以看到，文章中所提出的平衡权重优化以及几何重投影误差对定位精度有提升作用。

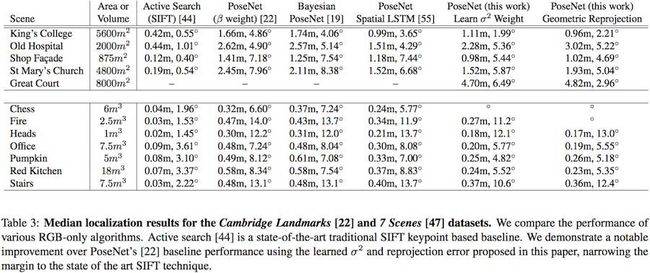
2.2.3 与基于特征的定位方法进行对比

  该实验在Dubrovnik数据集上进行评测，取得了平均误差40m、中值误差7.9m的结果；而APE、P2F等基于特征的定位方法的评价误差为15m左右、中值误差在10m以下。由此可见，基于深度学习的单目相机位姿估计方法与基于特征的定位方法仍然差距较远，离实用和产品落地还有很长的路要走。同时，本文作者称结果差最主要是因为训练样本少而造成，由此也可见基于深度学习的单目相机位姿估计方法对训练样本的强依赖性，真正用于实际工程中将缺乏场景适应性。但基于深度学习的单目相机位姿估计方法依然有其优势，某些失败的例子，其能做的很好，同时不需要点云模型的维护，相应也减少了成本。

3 方法

3.1 基本损失函数

  采用欧式距离L2计算回归损失，损失函数（优化目标方程）如下：
$$loss(I)=||\hat{x}-x|{|}_2+\beta ||\hat{q}-\frac{q}{||q||}|{|}_2$$
  其中，$\beta$是权重平衡因子。

3.2 权重因子优化

  理想情况下，我们不希望存在权重平衡因子这一超参数（超参数设定对模型训练影响严重）就能够同时优化相机位置与姿态的损失。针对这一问题，作者提出了一种可以进行权重因子优化的方法，并将该方法基于同方差不确定（homoscedastic uncertainty，可以使用文献[20]中的概率深度学习方法进行学习）；同方差不确定可以不依赖输入数据而对不确定进行测量。利用同方差不确定，作者将损失函数变为如下形式：
$${\mathcal{L}}_{\sigma }(I)={\mathcal{L}}_x(I){\hat{\sigma }}_x^2+log{\hat{\sigma }}_x^2+{\mathcal{L}}_q(I){\hat{\sigma }}_q^2+log{\hat{\sigma }}_q^2$$
  该损失函数的设计理念是平衡位置损失与姿态损失数量级差距太大的问题。位置损失较大，将具有较大的同方差，因此损失函数的第一项会变小；而姿态损失较小，将具有较小的同方差，异常损失函数第三项会变大；而第二、四项是为了防止一、三项不确定性为无穷大的情形出现（此时的损失函数为0，梯度将变为0），此时第二、四项将对不确定性进行惩罚。在实践中，作者做了如下处理：
  令$\hat{s}:=log{\hat{\sigma }}^2$，损失函数变换为如下形式：
$${\mathcal{L}}_{\sigma }(I)={\mathcal{L}}_x(I)exp(-{\hat{s}}_x^2)+{\hat{s}}_x^2+{\mathcal{L}}_q(I)exp(-{\hat{s}}_q^2)+{\hat{s}}_q^2$$
  该损失函数选择指数函数代替对数函数，能避免除零问题；作者所使用损失函数鲁棒性较好，所有实验均选取${\hat{s}}_x^2=0.0$、${\hat{s}}_q^2=-3.0$。

3.3 几何重投影误差项的引入

  利用相机内参以及相机位姿可以实现图像像素2D点到3D坐标点的转换，作者进一步增加此约束形成几何重投影误差，具体形式如下：
$${\mathcal{L}}_g(I)=\frac{1}{|{\mathcal{G}}^{{}^{\prime }}|}\sum _{g_i\in {\mathcal{G}}^{{}^{\prime }}}||\pi (x,q,g_i)-\pi (\hat{x},\hat{q},g_i)|{|}_{\gamma }$$
  其中$g_i\in {\mathcal{G}}^{{}^{\prime }}$是场景中的三维坐标点。

3.4 鲁棒核函数的使用

  本文作者采用核函数$||.|{|}_{\gamma }$刻画损失函数，具有更好的鲁棒性，常用的鲁棒核函数包括：Huber函数和Tukey函数。

4 结论与评价

  本文所介绍论文对PoseNet的损失函数进行了改进，引入了权重因子优化
和几何几何重投影误差，提高了深度学习估计单目图像位姿的性能。实验结果表明，该论文提出的改进方法提升了PoseNet的性能，但相对于PoseNet方法，其精度依然较差；同时也可以看到，基于深度学习估计单目图像位姿的方法，具有更高的时间效率和鲁棒性。因此，个人认为基于深度学习估计单目图像位姿的方法依然存在大量调整，宏观来说，模型精度较低，难以实用；微观来讲，存在模型结构设计不完善、视觉几何相关知识结合不够等待思考的问题。