摘要: 本文详细介绍了空间变换网络及其工作原理,最后将整个机制归结为两个熟悉的概念:仿射变换和双线性插值。
纯干货:深度学习实现之空间变换网络-part1
在第一部分中,我们主要介绍了两个非常重要的概念:仿射变换和双线性插值,并了解到这两个概念对于理解空间变换网络(Spatial Transformer Networks)非常重要。
在这篇文章中,我们将详细介绍一篇空间变压器网络这一论文——Go
ogle Deepmind的研究人员Max Jaderberg,Karen Simonyan,Andrew Zisserman和Koray Kavukcuoglu最早提出了这一概念。
读完本文,希望你能够对这个模型有一个清晰的认识和理解。我们将在后续第三部分中使用Tensorflow实现该网络。
目的
在进行分类任务时,我们通常希望系统对变化的输入具有较强的鲁棒性。 也就是说,如果输入需要经过某种“转换”,我们的分类模型理论上应该在转换之前输出相同的类标签。一般情况下,图像分类模型可能会面临以下“挑战”:
1.规模变化:现实世界和图像中的尺寸变化。
2.视角变化:随着观察者的角度变化,物体的取向不同。
3.变形:非刚体可以变形并扭曲成不寻常的形状。
对于人类来说,将上图中的对象进行分类,这很简单。但是,计算机算法仅适用于原始3维亮度值数组,因此输入图像的微小变化也可能会改变相应数组中的像素值。因此,理想的图像分类模型理论上应该能够从纹理和形状中分离出物体的形态和变形,如下面的猫咪图像。
如果我们的模型可以使用某种组合来从左到右执行,从而简化后续的分类任务,那么这是不是非常理想?
池化层
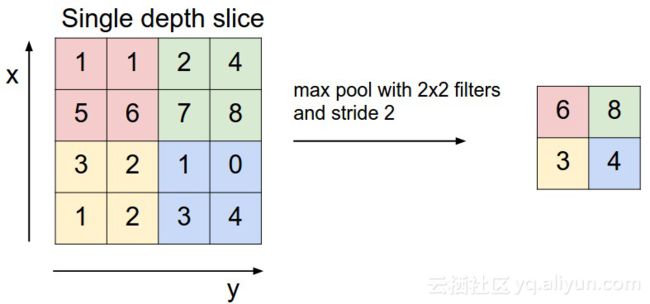
事实证明,我们在神经网络架构中使用池化层,这使模型具有一定程度的空间恒定性。池化操作也是一种降采样机制,它逐层降低了深度维度上特征映射的空间大小,同时也减少了参数的数量和计算成本。
池化层在空间上对数组进行下采样。上图中,左图为大小为[224*224*64]的输入数组与维度为2、步长为2的滤波器做最大池化操作,输出大小为[112*112*64]的数组。右图为2*2的最大池化数组。
它是如何具有恒定性的?我们可以这样理解,池化的思想是采用复杂的输入,将其分解为一个个单元,并将这些复杂单元中的信息“池化”,产生一组更简单的单元集,来描述输出。举例来说,假设我们有3张数字7的图片,每张图片的方向不同。我们通过聚合像素值可以捕获到大致相同的信息,因此不管数字在网格中的哪个位置,每张图像网格上的池化都会检测到数字7。
池化之所以不受欢迎,有以下限制因素。首先,池化具有破坏性。在使用池化时,75%的特征激活会面临丢失,这就意味着我们会丢失确切的位置信息。由于我们之前提到过,池化赋予了网络一定的空间鲁棒性,而位置信息在视觉识别中尤为重要。想想上面提到的猫咪分类器,相对于鼻子的位置,知道胡须的位置可能更重要。当我们使用最大池化时,这些信息就已经丢失了。
池化的另一个限制因素是,它是本地和预定义的。由于感受野较小,池化操作只会对网络的更深层产生影响,这就意味着中间特征映射可能会有更大的输入失真。请记住,由于只增加感受野会过于降低我们的特征映射,因此,我们不能随意的只增加感受野。
另外一个主要的问题就是,对于相对较大的输入失真,卷积网络并不是恒定的。这种限制源于,只有一个用于处理数据空间变化的受限预定义池化机制。这就是空间变换网络发挥作用的地方!
Geoffrey Hinton曾表示:在卷积神经网络中使用池化操作是一个很大的错误,并且网络能够稳定运作本身也是一场灾难。
空间变换网络(STNs)
通过为卷积神经网络提供确切的空间变换,空间变换机制解决了上述问题,它拥有3个属性。
1.模块化:只需要进行微小的调整,就可以将空间变换网络插入到现有体系结构的任何地方。
2.可区分性:可以使用反向传播算法进行训练,允许对所插入的模型进行端到端的训练。
3.动态的:在每个输入样本的特征映射上执行主动空间变换,而池化层则是对所有输入样本进行操作。
正如你所看到的,空间变换在所有方面都优于池化运算符。那么,什么是空间变换呢?
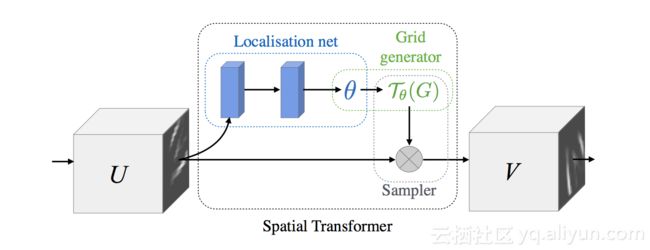
如上图所示,空间变换模块由三个部分组成:一个定位网络(localisation network),一个网格生成器(grid generator )和一个采样器(sampler)。我们不能盲目的对输入图像进行仿射变换,首先需要创建一个采样网格,对其进行转换,然后使用网格对输入图像进行采样,这一点非常重要。下面我们来看一下空间变换的核心部分。
定位网络
定位网络是作用于输入特征映射,输出仿射变换参数θ。其定义如下:
1.输入:形状为(H,W,C)的特征映射U。
2.输出:形状为(6,)的变换矩阵θ。
3.架构:全连接网络或卷积网络。
在训练网络时,我们希望定位网络能够输出越来越精确的θ。精确意味着什么呢?试想一下数字7逆时针旋转90度。经过2次训练以后,定位网络能够输出一个变换矩阵,来执行45度的顺时针旋转,经过5次训练以后,实际上可以学习完成90度的顺时针旋转。我们的输出图像看起来就像一个标准数字7,这是我们的神经网络在训练数据中看到的,并且可以对其进行轻松的分类。
另一种方式则是,定位网络学习存储如何将每个训练样本转换为其所在层的权重。
参数化的采样网格
网格生成器的作用是输出一个参数化的采样网格,这是一组点集,即输入映射经过采样产生期望的转换输出。
具体来说,网格生成器首先创建与输入图像U(格式为(H,W))相同大小的归一化网格,即覆盖整个输入特征映射的一个索引集(xt,yt)映射(上标t代表输出特征映射的目标坐标)。由于我们对这个网格做了仿射变换,并且想要使用变换,我们继续在坐标矢量上添加一行进行计算。最后,我们将6个参数θ塑造为一个2*3矩阵,并执行下面的乘法运算,就会得到我们所需要的参数化采样网格。
输出的列向量包含一组索引,告诉我们应该在哪里对输入进行采样,就能得到所需的转换输出。但是,如果这些指数是分数呢?这就是即将要介绍双线性插值的原因。
可微分的图像采样
由于双线性插值是可微的,因此非常适用于空间变换网络。通过输入特征映射和参数化采样网格,我们进行双线性采样并获得形状为(H',W',C')的输出特征映射V。这就意味着,我们可以通过指定采样网格的形状,来执行下采样和上采样。我们绝对不仅限于双线性采样,还可以使用其他的采样内核,但重要的一点是:它必须是可微的,以便允许损失梯度一直流回的定位网络。
上述为空间变换的内部工作原理,可将其归结为我们一直在谈论的两个关键概念:仿射变换和双线性插值。我们让网络学习最佳的仿射变换参数,这将有助于独立完成分类任务。
有趣的空间变换
最后,我们来举两个例子,说明下空间变换的应用。
失真MINIST数据集
下图是将空间变换作为全连接网络的第一层,对失真MNIST数据集的数字进行分类的结果。
注意它是怎样学会理想的“鲁棒性”图像分类模型?通过放大和消除杂乱的背景,将输入进行“标准化”进行分类。如果你想查看变换的实时动画,请点击这里。
德国交通标志识别GTSRB数据集
总结
本文概览了Google Deepmind的空间变换网络论文。我们首先介绍了分类模型所面临的挑战,主要是输入图像失真导致分类失败。一种解决方案是使用池化层,但是有明显的局限性——使用率很低。另一个解决方案就是本文的空间变换网络。
这其中包含一个可微的模块,可以插入到卷积网络中任何一个位置以增加其几何不变性。它赋予了网络空间变换特征映射,而无需额外增加数据或监督成本。最后,整个机制归结为两个熟悉的概念:仿射变换和双线性插值。
以上为译文。
本文由阿里云云栖社区组织翻译。
文章原标题《Deep Learning Paper Implementations: Spatial Transformer Networks - Part II》,译者:Mags,审校:袁虎。
详细内容请查看原文。