论文阅读:High-Precision Depth Estimation Using Uncalibrated LiDAR and Stereo Fusion
论文阅读:High-Precision Depth Estimation Using Uncalibrated LiDAR and Stereo Fusion
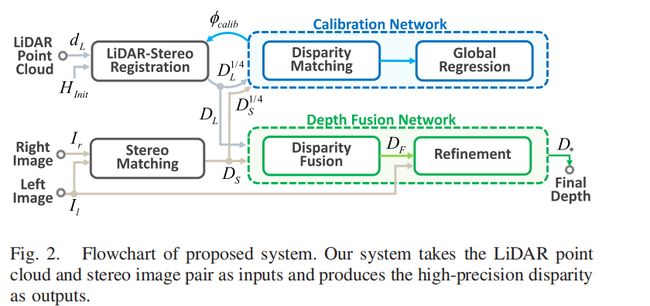
本文提出了一个用于未校准的LiDAR和双目融合的用于深度估计的方法,本文的网络由三部分组成:
校准模块、融合模块和优化模块
摘要:
我们解决了从未校准的LiDAR点云和立体图像进行3D重建的问题。由于单独使用每个传感器进行三维重建在密度和精度方面存在弱点,我们提出了一种用于高精度深度估计的深度传感器融合框架。该体系结构由校准网络和深度融合网络组成,这两个网络的设计都考虑了移动设备的精度和效率之间的权衡。校准网络首先校正初始外部参数以对准输入传感器坐标系。通过在深度域中进行定标,显著提高了定标精度。在深度融合网络中,对稀疏LiDAR和密集立体深度的互补特性进行Boosting编码。由于LiDAR和立体深度融合的训练数据相当有限,我们介绍了一种从原始Kitti数据集生成伪地面标签的简单而有效的方法。实验评估结果表明,该方法在Kitti基准测试中的性能优于目前最先进的方法。我们还使用我们专有的多传感器采集平台收集数据,并验证所提出的方法是否适用于不同的传感器设置和场景。
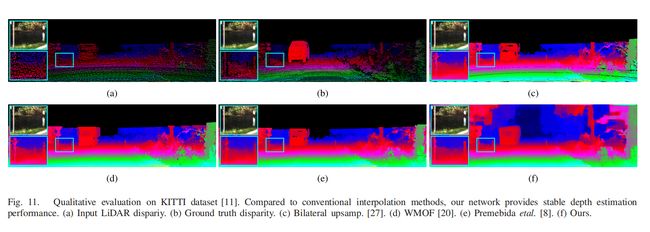
效果图:
网络结构
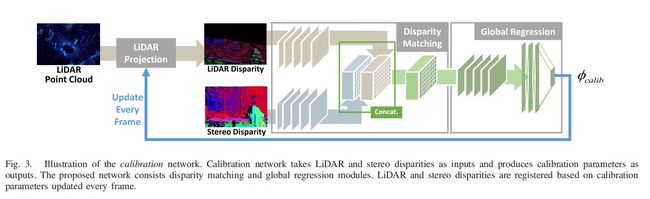
校准网络
文章先将LiDAR得到的点云通过一个初始的但是不精确的外参矩阵 H i n i t H_{i n i t} Hinit投影到双目的左图上:
[ u , v , 1 ] T = P H i n i t ϕ c a l i b − 1 [ x , y , z , 1 ] [u, v, 1]^{T}=P H_{i n i t} \phi_{c a l i b}^{-1}[x, y, z, 1] [u,v,1]T=PHinitϕcalib−1[x,y,z,1]
其中 [ x , y , z , 1 ] [x, y, z, 1] [x,y,z,1] 是由LiDAR得到的三维点云的坐标,$[u, v, 1] $ 是图像坐标系 , P是内参矩阵 ,而 ϕ calib − 1 \phi_{\text {calib}}^{-1} ϕcalib−1是用于校准初始外参矩阵的矩阵 ϕ calib = [ R ( r x , r y , r z ) [ t x , t y , t z ] 2 0 1 ] \phi_{\text {calib}}=\left[\begin{array}{cc} \mathcal{R}\left(r_{x}, r_{y}, r_{z}\right) & {\left[t_{x}, t_{y}, t_{z}\right]^{2}} \\ 0 & 1 \end{array}\right] ϕcalib=[R(rx,ry,rz)0[tx,ty,tz]21], ϕ calib − 1 \phi_{\text {calib}}^{-1} ϕcalib−1会随着每一帧迭代的更新。
本文先将LiDAR点云的深度信息通过 D L ( u , v ) = b s f u / x D_{L}(u, v)=b_{s} f_{u} / x DL(u,v)=bsfu/x 转换成视差值 ,这样就可以将原来的深度和视差的 different modality data 问题解决了 , 通过深度值转换成视差值就把问题都放在了disparity domain去解决 , 作者认为这种方法可以提高校准的准确性和效率。
视差匹配模块:从 D L 1 / 4 D_{L}^{1 / 4} DL1/4和 D S 1 / 4 D_{S}^{1 / 4} DS1/4中提取中间特征,分别从 D L D_L DL和 D S D_S DS向下采样,缩放因子为4,并通过级联和卷积层组合以估计它们的特征对应性 ,作者解释向下采样是为了在保证高精度的同时对于highly textured surfaces and shadows更加鲁棒, 同时对于相机模型的变化也会更加鲁棒。
校准网络每帧都会更新校准参数,并且输入的视差图会在LiDAR投影模块中重新调整为原始图像分辨率。
深度融合网络
深度融合网络由两个级联子模块组成,包括视差融合和优化。 该体系结构设计的灵感来自以下两种直觉:1)3D LiDAR视差和双目视差可以提供互补的线索,以帮助重构高精度视差,以及2)RGB 图像可以用来提高视差估计性能。
两个要点:
融合模块使用了膨胀卷积的U-Net结构,优化模块预测的是一个残差用于精修深度图。
训练
- 校准网络 :用于训练校准网络的数据来自于KITTI的校准数据集,通过随机的添加噪声 θ g t θ_{gt} θgt 来造成偏移,只要就可以得到无限的校准数据集。
- 融合模块: 尽管KITTI数据集提供了来自原始Velodyne扫描的深度信息,但是来自单个帧的3D点云的密度不足以训练基于CNN的深度融合模型。此外,需要大量的人工来消除由于遮挡物和动态物体引起的噪声。 为了克服这些局限性,我们累积了之前的11个3D点云帧,以增加生成的视差图DV的密度。 当发生冲突值时,我们选择最接近颜色捕获时间的视差。 参考框架是使用颜色引导插值独立插值的,尽管颜色引导插值会导致纹理复制伪影,但对于遮挡和动态对象的异常值却很鲁棒。 因此,我们使用了插值参考系来确定地雷离群点,并通过去除它们来清除DV。使用此简单技术可以删除DV中的大多数异常值。
损失函数
损失函数由三部分组成:
L = L Φ C + L Φ F + L Φ R \mathcal{L}=\mathcal{L}_{\Phi_{C}}+\mathcal{L}_{\Phi_{F}}+\mathcal{L}_{\Phi_{R}} L=LΦC+LΦF+LΦR
其中
L Φ C = ∣ θ calib − θ g t ∣ 1 \mathcal{L}_{\Phi_{C}}=\left|\theta_{\text {calib}}-\theta_{g t}\right|_{1} LΦC=∣θcalib−θgt∣1
L Φ F = ∑ p ∈ Ω ( D V ) ∣ D F ( p ) − D V ( p ) ∣ 1 + λ ∑ p ∈ Ω ( D S ) ∣ D F ( p ) − D S ( p ) ∣ 1 \begin{aligned} \mathcal{L}_{\Phi_{F}}=\sum_{p \in \Omega\left(\mathcal{D}_{V}\right)} | D_{F}(p) &-\left.\mathcal{D}_{V}(p)\right|_{1}&+\lambda \sum_{p \in \Omega\left(\mathcal{D}_{S}\right)}\left|D_{F}(p)-\mathcal{D}_{S}(p)\right|_{1} \end{aligned} LΦF=p∈Ω(DV)∑∣DF(p)−DV(p)∣1+λp∈Ω(DS)∑∣DF(p)−DS(p)∣1
L Φ R = ∑ p ∈ Ω ( D V ) ∣ ( D R ( p ) + D F ( p ) ) − D V ( p ) ∣ 1 + λ ∑ p ∈ Ω ( D S ) ∣ ( D R ( p ) + D F ( p ) ) − D S ( p ) ∣ 1 \begin{aligned} \mathcal{L}_{\Phi_{R}}=& \sum_{p \in \Omega\left(\mathcal{D}_{V}\right)}\left|\left(D_{R}(p)+D_{F}(p)\right)-\mathcal{D}_{V}(p)\right|_{1} \\ & \quad+\lambda \sum_{p \in \Omega\left(\mathcal{D}_{S}\right)}\left|\left(D_{R}(p)+D_{F}(p)\right)-\mathcal{D}_{S}(p)\right|_{1} \end{aligned} LΦR=p∈Ω(DV)∑∣(DR(p)+DF(p))−DV(p)∣1+λp∈Ω(DS)∑∣(DR(p)+DF(p))−DS(p)∣1