扫描线填充多边形算法详解与代码
扫描线填充多边形算法详解与代码
首先给出已知信息:多边形结构体里面包含三个信息:顶点个数,顶点和颜色
class MyPolygon
{
public:
int m_VerticeNumber;
CPoint m_Vertex[50];
COLORREF m_LineColor;
}思路:
找到多边形的最小y值和最大y值,然后用这个范围内的每一条水平线与多边形相交,通过得到的交点画线段,由此填充整个多边形。
具体通过交点画线段:
1.对存储交点的数组进行排序(从小到大)
2.数组中数据两两一对,填充每对交点间的线段
这样分析下来我们所要做的只有两件事,一是求出扫描线与多边形边的交点,二是对交点数组进行排序。
接下来开始一个一个分析:对于求扫描线与多边形的交点,需要考虑到以下几个特殊情况:
1.扫描线与边重合

2.扫描线与边的交点为顶点
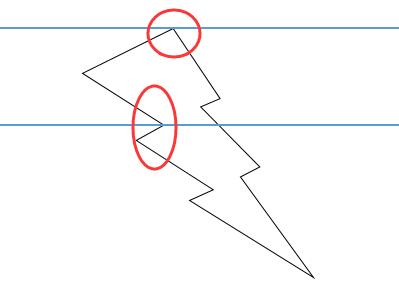
具体情况具体分析咯:
对于扫描线与边重合,只需要判断该边的两个顶点的y值是不是一样的,是一样的表示该边水平,因此可以直接重画这条线。否则继续之后的判断。
对于扫描线与顶点重合,大家看上面的图,我画了两种情况,一种是局部极值的顶点,一种不是局部极值的顶点,这两种顶点交点的记录方法还不一样。如果交点是顶点,且为局部极值,这个交点要被连续记录两次;如果交点是顶点,且不是局部极值,这个交点只需要被记录一次。大家可以看图想想,当交点是局部极值顶点是,所要描绘的线段就是该交点,所以记录两次;当交点是顶点,不是局部极值,所要描绘的是该顶点交点到下一个交点这一条线段,所以只能记录一次。
判断一个顶点是否为局部极值,可以通过与顶点关联的两条边的另外两个顶点来判断,通过判断它们是不是在顶点交点的同一侧来得出顶点的极值性:


排序算法:随机快速排序
下面贴上代码:
int getMiny(MyPolygon ThePolygon)
{
int min = ThePolygon.m_Vertex[0].y;
for(int i = 1;iif(min>ThePolygon.m_Vertex[i].y)
min = ThePolygon.m_Vertex[i].y;
return min;
}
int getMaxy(MyPolygon ThePolygon)
{
int max = ThePolygon.m_Vertex[0].y;
for(int i = 1;iif(maxreturn max;
}
//交换
void Swap(int *a,int i,int j){
int temp=a[i];
a[i]=a[j];
a[j]=temp;
}
//随机快速排序
int qsort(int *a,int begin,int end){
int i,j,temp;
i=begin-1;j=begin;
for(;jif(a[j]<=a[end-1])
Swap(a,++i,j);
}
return i;
}
void randqsort(int *a,int begin,int n){
while(begin>=n)
return ;
srand((unsigned)time(NULL));
int key=(begin+rand()%(n-begin));
Swap(a,key,n-1);
int m=qsort(a,begin,n);
randqsort(a,begin,m);
randqsort(a,m+1,n);
}
void ScanFill(CDC *pDC,MyPolygon ThePolygon, CPoint startPoint, COLORREF fillCol)
{
int miny,maxy;
int sx,sy,tx,ty;
miny = getMiny(ThePolygon);
maxy = getMaxy(ThePolygon);
int *index = new int[100];
int *judge = new int[ThePolygon.m_VerticeNumber];
memset(index,-1,sizeof(int)*100);
memset(judge,0,sizeof(int)*ThePolygon.m_VerticeNumber);
int x;
CPoint Point;
for(int i = miny;i<=maxy;i++)
{
//记录扫描线与边线的交点
int temp = 0;
for(int i1 = 0, l = ThePolygon.m_VerticeNumber , j1 = l - 1; i1 < l; j1 = i1, i1++) {
sx = ThePolygon.m_Vertex[i1].x;
sy = ThePolygon.m_Vertex[i1].y;
tx = ThePolygon.m_Vertex[j1].x;
ty = ThePolygon.m_Vertex[j1].y;
int lowy,heighty;
lowy = (syty)?sy:ty;
//水平线
if(ty == sy)
{
if(i == ty)
{
int xmax,xmin;
xmax = (sx>tx)?sx:tx;
xmin = (sxfor(int xx = xmin;xx<=xmax;xx++)
{
Point.x = xx;Point.y = i;
pDC->SetPixelV(Point, fillCol);
}
}
continue;
}
//没有交点
if(iheighty)
continue;
x = sx + (i - sy) * (tx - sx) / (ty - sy);
//判断交点(x,i)是不是顶点
if((x == ThePolygon.m_Vertex[i1].x&&i == ThePolygon.m_Vertex[i1].y))
{
//判断顶点是不是极值点
//即判断与交点相关联的两条线的另外两个顶点是不是在交点的同一侧
if(i1!=l-1&&judge[i1] == 0){
if((i-ThePolygon.m_Vertex[i1+1].y)*(i-ThePolygon.m_Vertex[j1].y)<0)//异号
index[temp++] = x;
else//同号 极值点 记录两次
{
index[temp++] = x;
index[temp++] = x;
}
}
else if(i1 == l-1&&judge[i1]==0)
{
if((i-ThePolygon.m_Vertex[0].y)*(i-ThePolygon.m_Vertex[j1].y)<0){//异号
index[temp++] = x;
}
else//同号 极值点 记录两次
{
index[temp++] = x;
index[temp++] = x;
}
}
judge[i1] = 1;
continue;
}
else if((x == ThePolygon.m_Vertex[j1].x&&i == ThePolygon.m_Vertex[j1].y))
{
if(j1 != 0&&judge[j1]==0){
if((i-ThePolygon.m_Vertex[i1].y)*(i-ThePolygon.m_Vertex[j1-1].y)<0){//异号
index[temp++] = x;
}
else//同号 极值点
{
index[temp++] = x;
index[temp++] = x;
}
}else if(j1 == 0&&judge[j1]==0)
{
if((i-ThePolygon.m_Vertex[i1].y)*(i-ThePolygon.m_Vertex[l-1].y)<0)//异号
index[temp++] = x;
else//同号 极值点
{
index[temp++] = x;
index[temp++] = x;
}
}
judge[j1] = 1;
continue;
}
//交点不是顶点
index[temp++] = x;
}
//将index排序
randqsort(index,0,temp);//随机快速
//填充多边形
for(int n=0,m=n+1;mindex[n]!=-1;n+=2,m=n+1)
{
for(int xx = index[n];xx<=index[m];xx++)
{
Point.x = xx;Point.y = i;
pDC->SetPixelV(Point, fillCol);
}
}
//清零
for(int k=0;k<100;k++)
index[k] = -1;
}
delete[] index;
delete[] judge;
} 减少计算量。在绘制直线时,有一种DDA算法,它是利用(x,y)直接求出下一个点位于(x+1,y+m)或者(x+1/m, y+1)。在这里可以利用这一点。当已经得到y = e和多边形所有边的交点时,对于下一条扫描线y=e+1,如果没有新边与y=e+1相交,就可以推出y = e+1 和多边形所有边的交点。上述代码中没有实现这一点
