论文阅读笔记:《PatchMatch: A Randomized Correspondence Algorithm for Structural Image Editing》

摘要

  提出了一种基于随机化算法的交互式图像编辑工具，用于在两张图片之间快速寻找对应的小区域。该算法的主要看法是，可以通过随机采样找到一些好的 patch 匹配，根据图像的自然一致性允许我们将这种匹配快速传播到周围区域。这个简单的算法构成了多种工具的基础 — 图像重定向 (不引入大的畸变的情况下，通过改变照片的大小和比例信息，来适应各种尺寸屏幕)、图像修补、图像重组。

简介

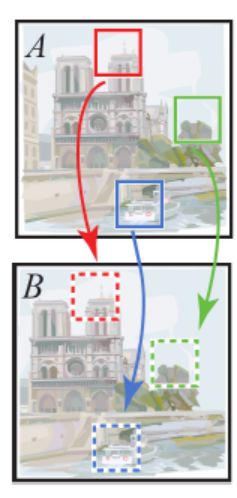
  非参 patch 采样方法思想是在 patch distance 度量下，为 A 中的每个 patch 找到 B 中最近的邻居，这种映射叫最近邻域 (Nearest-Neighbor Field) 。图像和 patch 大小分别为 M 和 m 个像素 , 用蛮力搜索算法时间复杂度为 $O\left(m{M}^2\right)$ ,即使使用近似最近邻和降维等加速方法，这个搜索步骤仍然是非参数 patch 采样方法的瓶颈。此外，基于树结构的加速方法使用较大存储空间 O（M），这限制了它们对高分辨率图像的应用。
  为了有效地计算近似最近邻域，本文提出的新算法依赖三个观察。偏移空间维度，虽然 patch 空间的维数很大 (m 维)，但是它是稀疏填充的。之前的许多方法都是通过使用树结构 (kd-tree在 $O(mM\log M)$ 时间内搜索) 和降维方法 ( PCA) 来减少patch 空间的维数来加速最近邻搜索。我们的算法在可能的 patch 偏移量的二维空间中进行搜索，从而获得更快的速度和内存效率。图像的自然结构，通常对每个像素的独立搜索忽略了图像的自然结构。利用 patch 算法时，输出通常包含来自输入的大量连续数据块 。因此，我们可以通过以一种相互依赖的方式对相邻像素进行搜索来提高效率。大数定律，虽然任何一个随机分配的 patch 都不太可能是一个很好的猜测，但总有差不多的。且随着随机分配范围的变大，不具有正确偏移的 patch 可能性变得很小。
  基于这三个观察结果，提出了一种近似 NNFs的使用增量更新计算的随机算法。该算法从初始猜测(先验信息或随机field)开始。迭代过程包括两个阶段：传播阶段，利用相关性将好的解传播给场中相邻的像素点；随机搜索，当前偏移向量受到多个随机偏移量的影响。对测试图像的收敛速度可达 2MP。与主成分分析的 kd-tree 相比，CPU 实现速度提高了 20-100 倍。此外，还提出了一种 GPU 实现，对于类似的图像大小，它的速度大约是 CPU 版本的 7 倍。算法除原始图像外只需很少的额外内存，不像以前的算法构建辅助数据结构来加速搜索。使用默认参数设置，运行时间效率为 $O(mM\log M)$ ，内存使用量为 $O(M)$。虽然这与基于树的加速技术具有相同的渐近时间和存储率，但是实际上更小。
  在第 4 节中，我们演示了该算法在具有三种交互编辑模式的结构化图像编辑程序中的应用：图像重定向、图像补全和图像重组。允许用户直观的进行交互约束合成过程。

相关工作

纹理合成与重组

  Efros 和 Leung [1999] 提出了一种简单的非参数纹理合成方法，该方法通过从纹理实例中采样小块并粘贴到合成图像中。& [ Wei 和 Levoy 2000 ; Ashikhmin 2001; liang 2001; Kwatra et al. 2003; criisi et al. 2003 ; Drori et al. 2003 ] 改进了搜索和采样方法，以更好地保存结构。& 上述贪心算法在填充复杂结构的大孔有时顺序会不一致，Wexler 等 [2007] 将此问题表述为全局优化问题从而获得全局一致性的重组结果。该迭代多尺度优化算法反复并行搜索所有孔像素的最近邻 patch。该算法最初的实现通常比较慢 (对于小于 1 MP 的图像需几分钟)。& 基于 Patch 优化的方法已经成为纹理合成的常用方法 [Kwatra et al. 2005; Kopf et al. 2007; 魏 et al. 2008] 。Lefebvre 和 Hoppe [2005] 使用了相关的并行更新方案，甚至演示了基于 GPU 的实时实现。& Komodakis 和 Tziritas [2007] 提出了另一种全局优化算法来重组图像，该算法使用带有自适应优先级消息传递机制的循环信念传播。虽然该方法取得了很好的效果，但其速度相对较慢，仅在小图像上适用。

最近邻搜索方法

  高质量的 patch 优化方法复杂度高 (进行更多的搜索迭代)，已经提出了各种加速搜索的方法。& 通常涉及到树结构，如 TSVQ [Wei 和 Levoy 2000]、kd-trees [Hertzmann et al. 2001 ; Wexler et al. 2007 ; Kopfet et al. 2007] 和 VP -trees [Kumar et al. 2008]，它们都支持精确搜索和近似搜索 (ANN)。& 在综合应用中，近似搜索常与 PCA 等降维技术结合使用 [ Hertzmann et al. 2001; Lefebvre and Hoppe 2005 ; Kopf et al. 2007 ]，因为 ANN 方法在低维度下时间效率和内存效率更高。& Ashikhmin [2001] 提出了一种利用合成过程中的局部相干性的局部传播技术，将 patch 的搜索空间限制在范例纹理中源位置的相邻元素，本文方法受此启发。& k-coherence 技术 [Tong et al. 2002] 将传播思想与预计算阶段相结合，缓存每个 patch 的 k 个最近邻，以后的搜索将利用这些预计算集。虽然这加快了搜索阶段，但是 k-coherence 仍然需要对输入中的所有像素进行完整的最近邻搜索，并且只用合成纹理的数据进行了演示。假设初始偏移量足够接近，只搜索少量最近的邻居就行，对于输入是小的纯纹理，可能正确，但对大的复杂图像，本文的随机搜索阶段 (规避局部极小值) 是必要的。

控制和交互

  patch 采样方案的一个优点是提供足够的精细控制。例如，在纹理合成中，Ashikhmin [2001] 的方法通过初始化具有所需颜色的输出像素，让用户控制过程。Hertzmann 等人 [2001] 的图像类比框架使用辅助图像作为 “指导层”，实现多种效果，包括超分辨率、纹理传输、艺术过滤器和按数字纹理。在图像补全领域，通过对缺失区域内外的结构进行标注，得到了令人印象深刻的引导填充结果 [Sun et al. 2005]。…

图像重定向

  许多图像重定向方法都采用 warping 或 cropping，使用一些显著性度量来避免重要的图像区域变形 [Liu and Gleicher 2005; Setlur et al. 2005;Wolf et al. 2007;Wang et al. 2008]。& Seam carving (线裁剪) [Avidan and Shamir 2007;Rubinstein 等人 2008] 使用一种简单贪婪的方法对图像中的 seam 进行优先排序，而这些 seam 在重新定位时可以很好的移除。虽然线裁剪速度很快，但它不能很好地保存结构，且只能对结果提供有限的控制。& Simakov et al. [2008] 提出将图像和视频重定向问题框架为原始图像和输出图像中小块之间双向相似性的最大化，与 Seam carving 方法比特别慢。Wei et al. [2008] 提出了一种类似的目标函数和优化算法，主要是生成纹理信息以加快合成的方法。& 本文的约束重定向和图像重组应用程序使用与 Simakov 相同的目标函数和迭代算法，使用我们的新最近邻算法来提高交互速度。& 之前的方法，用户控制主要是确保重要区域不失真。本文集成了用户特定约束，在重定向过程中，可控制均匀缩放或非均匀缩放，可将行或对象固定到特定的输出位置。

图像重组

  根据用户输入重新排列图像中的内容，Simakov et al. [2008] 和 Cho et al. [2008] 在 MRF 公式中使用了更大的图像块和信念传播进行重组。重组需要最小化全局误差函数，因为对象可能会移动很长的距离，而贪婪算法会加大工作量。

加权最近邻算法

  我们将一个 nearest-neighbor field (NNF) 定义为函数 $f:A\mapsto {\mathbb{R}}^2$ f 表示两个 patch 某种距离函数，此处表示偏移量 。定义在图像 A 中所有可能的 patch 坐标 (patch center 的位置)。给定 A 图中一 patch 坐标 a 及对应 B 图中最近邻 patch 坐标 b 。f (a) 就是 b - a 。我们将 f 的值称为偏移量，它们存储在一个和A 维数相同的数组中。
  本节介绍一种随机加权 NNF 算法。这个算法的关键是在可能的偏移量空间中搜索，相邻的偏移量协同搜索，甚至一个随机偏移量也可能是 patch 的一个很好的猜测。该算法有三个主要组件如图 2 所示。首先最近邻字段要么填充随机偏移量，要么填充一些先验信息。然后，对 NNF 应用迭代更新过程，将好的 patch 偏移量传播到相邻的像素，然后在邻域内随机搜索找到目前为止的最佳偏移量。

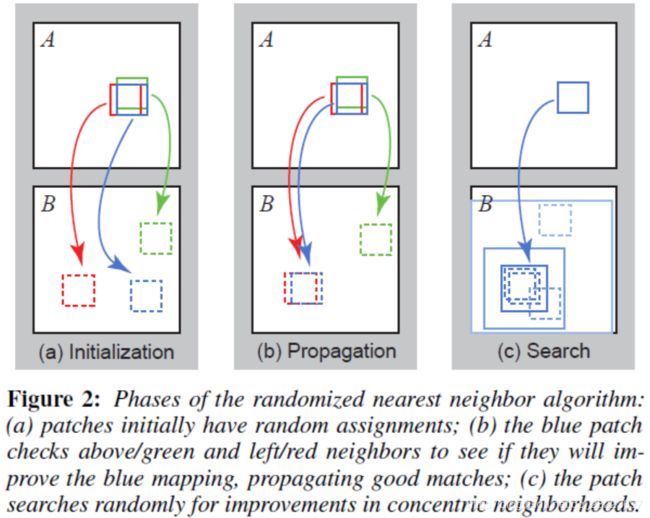
初始化

  最近邻域可以通过为该邻域分配随机值或使用先验信息来初始化。当使用随机偏移进行初始化时，我们在整个图像 B 范围内使用独立的均匀抽样。在实际应用时初始化范围可以由粗到细调节，粗范围有先验信息但是容易陷入局部最优。随机初始化先迭代一会，然后在 D 小的 patch 上与上次采样的 patch 合并，然后执行剩余的迭代。

迭代

  初始化之后，执行一个迭代过程来改进 NNF。算法的每次迭代过程如下：按扫描顺序检查偏移量 (从左到右，从上到下)，然后进行传播、进行随机搜索。这些操作在 patch 级别交叉进行： Pj 和 Sj 表示 patch j 上的传播和随机搜索，那么我们按照 P1;S1; P2;S2 … Pn;Sn 顺序进行。
  传播 用 $f(x-1,y)$ 和 $f(1,y-1)$ 偏移来改善 $f(x,y)$ 。设 $D(v)$表示 A 图中的像素 $(x,y)$ 处的 patch 与 B图 中像素 $(x,y)+v$ 处 patch 之间的距离(误差)。我们将 $f(x,y)$ 的更新为 $\{D(f(x,y)),D(f(x-1,y)),D(f(x,y-1))\}$ 中最小的。
  如果 $(x,y)$ 具有正确的映射，则它相关区域 R 中 $(x,y)$ 右下方的所有区域将被正确的映射填充。此外在偶数迭代中，我们通过反向描扫顺序，使用 $f(x+1,y)$ 和 $f(x,y+1)$ 作为我们的候选偏移。
  随机搜索 设 ${\mathbf{v}}_0=f(x,y)$ 为了提高 $f(x,y)$ ,测试从 v0 到一个指数递减距离的候选偏移量序列:
$${\mathbf{u}}_i={\mathbf{v}}_0+w{\alpha }^i{\mathbf{R}}_i$$
  ${\mathbf{R}}_i$ 是 $[-1,1]\times [-1,1]$ 中的均匀随机变量，$w$ 是最大搜索半径，$\alpha$ 是搜索窗口大小之间的固定比例。我们检查 i = 0,1,2… 的 patch，直到当前搜索半径 $w{\alpha }^i$ 小于1像素。我们设置 $w$ 为图像最大维度，$\alpha =1/2$。搜索窗口必须在B边界内。
  终止条件 迭代次数具体问题具体分析。这儿4-5次即可。
  效率 在传播和随机搜索阶段，当尝试用候选偏移 $u$ 改善偏移 $f(v)$时，如果 $D(u)$的部分和超过当前已知距离 $D(f(v))$，则可以提前终止。此外在传播阶段，当使用边长 $fp$ 和 $Lq$ 范数的方形 patch 时，通过在重叠区域的总和中注意冗余项，可以在 $O(p)$ 而不是 $O(p^2)$ 时间内递增地计算距离的变化。然而，这会产生额外的存储开销来存储当前最佳距离 $D(f(x,y)))$。
  GPU实现 第 4 节中描述的编辑系统依赖于 NNF 估计算法的 CPU 实现，为此，我们交替随机搜索和传播的迭代，其中每个阶段并行处理整个偏移量字段。虽然传播本质上是一个串行操作，但是我们采用了 Rong 和 Tan [2006] 的 jump flood方案来进行多个迭代的传播。在 GeForce 8800 GTS 卡上，GPU 算法在近似精度上大约比 CPU 算法快 7 倍。

合成数据分析

  …

真实数据分析

  …

编辑工具

…

结论、讨论、未来工作

 在图 10 中，现有的重定向方法都使照片中的两个子元素其中一个变形，而我们的系统允许我们简单地重组其中一个子元素，从而获得更多的空间进行重定向，并且以一种合理的方式自动重构背景。在图 11 中，我们看到 “seam carving” 在直线中引入了不可避免的几何扭曲，并压缩了重复的元素。而我们的方法允许显式地保留透视图行并省略重复元素。
 我们的算法本质上与 LBP 算法有一些表面上的相似之处，图割算法通常用于求解图像网格上的马尔可夫随机场 [Szeliski et al. 2008]。然而，它们有根本的区别：我们的算法是用来优化一个没有任何邻域项的能量函数。MRFs 经常使用这样一个邻域术语，基于底层生成模型中的一致性，用有噪声或丢失的数据对优化进行正则化。相比之下，我们的算法没有显式的生成模型，而是使用数据的一致性来修剪搜索，以寻找更简单的并行搜索问题的可能解决方案。因为我们的搜索算法在早期的迭代中找到了这些一致的区域，所以我们的匹配会偏向于一致。因此，即使没有显式地强制执行一致性，我们的方法对于许多实际的综合应用程序来说已经足够了。此外，我们的算法避免了昂贵的计算联合补丁兼容性项和推理 / 优化算法。
 我们的算法也有一些失败的例子。最值得注意的是，对于病理输入，如 3.3 节的合成图像用例，我们的收敛较差。此外，对图像进行极端编辑有时会产生 “重影” 或 “羽状” 伪影，而算法无法摆脱一个较大的局部最小盆地。然而，我们指出，我们的算法的速度使它可以引入额外的约束或简单地重新运行算法与一个新的随机种子，以获得一个不同的解决方案。
  通过在每个像素处使用队列，而不是计算单个最近邻居，可以计算 k 个最近邻居。这可能允许 k 相干策略与我们的算法一起使用。一般情况下，我们发现最优随机抽样模式和停止准则是函数的输入。对于一些输入，例如小的高度规则的纹理，较少或不需要随机搜索。对于其他具有大型结构的输入，如图 12 中所示，需要完全随机搜索。通过研究这些权衡并进一步研究 GPU 实现，可以实现额外的速度提升，从而在实时视觉和视频处理方面开辟新的应用。